气囊搬运圆筒的滚动阻力系数计算与测试

邓尚康，宋小强

（中交四航局第三工程有限公司，广东 湛江 524033）

气囊搬运重件施工工艺在重力式码头工程的构件搬运中已被熟练运用，在计算牵引力时，气囊的滚动阻力系数常采用0.03～0.05间的某一常数，本文通过理论公式计算了三种规格圆筒采用气囊搬动时的滚动阻力系数，并在搬运期间进行了阻力测试对比验证，得出气囊搬运时摩擦阻力系数不为常数，它与气囊囊体的弹性模量、气囊直径、预制场地坪及承受的线荷载有关，运用J.Halling滚动阻力公式计算的气囊滚动阻力系数能满足实际施工需要。

1 滚动摩擦力的理论计算公式

1.1 滚动阻力系数与气囊规格的关系

J.Halling对圆柱在平面上滚动的阻力公式进行了比较精确的推导，其推导的滚动阻力系数的公式为[1]：

式中：λ为滚动阻力系数；ε为滞后损耗系数；a为圆柱与平面接触宽度的一半（见图1）；R为圆柱半径；P为作用圆柱中心的荷载；L为圆柱与平面的接触长度；v1、E1分别为圆柱材料的泊松比及弹性模量；v2、E2分别为平面材料的泊松比及弹性模量。

图1 圆柱在平面上滚动时的接触面积

式中所用的滞后损耗系数ε不同于按简单拉伸试验获得的ε应变值，文献 [1]指出，在滚动过程中，材料任一单元接触区时的弹性变形是非常复杂的过程，而在简单拉伸中变形形式较为简单而均匀。文献认为滚动圆柱的滞后损耗系数约为作简单拉伸试验时获得应变值的3倍。气囊囊体是由帘线-橡胶组成的复合材料，它虽具有非线性弹性的性质，但在应变不大于7%以内仍可认为具有线弹性性质[2]，根据气囊弹性变形量的性能要求：用1.2倍工作压力作试验压力时，直径变形量不大于5%[3]，即气囊在工作压力Pe状态时的变形量为4.17%，滞后损耗系数ε可取12.5%。代入式（1）有式（3），Pe是指气囊顶升构件至工作高度时的压力计算值。

从式（2）可以看出，圆柱与平面的接触半宽a与圆柱承受的线荷载、圆柱直径及其材料特性有关。

气囊是属于大变形量的柔性体，其大变形只是断面形状发生变化，由于气囊工作压力是指在压扁后的压力，运行期间压力变化不大。由于囊体的应变较小，当气囊排气后可认为能恢复到原状，因此气囊仍可按弹性体考虑[4]，计算气囊与地坪的接触宽度时，由于气囊出厂时的检验报告没有囊体材料的弹性模量及泊松比值，可参考充气式轮胎变形及力学性能的试验参数[2]，取E1=0.66 MPa，泊松比v1=0.49，地坪的E2远大于E1，因此（1-v2）/E2一项在计算中可忽略不计，只需根据气囊的有关参数及承受的线荷载计算a值。

1.2 滚动阻力系数与牵引力的关系

气囊搬运时，气囊的受压状态可认为在平面上作无滑动的滚动，以气囊与重件为受力研究对象，见图2所示，为便于分析，所有支承气囊简化为相同工作高度的一根大气囊。

图2 气囊运行受力分析

气囊在水平面运行时，上部重件在牵引力Ft的作用下，克服气囊滚动阻力Ff移动。由于气囊与构件为同一系统，即气囊与构件底部接触的摩擦力不予考虑，根据平衡方程∑Fx=0，有：

忽略气囊自重，即有：

将式 （5）代入式 （4）有：

J.Halling对圆柱在平面上滚动阻力公式的推导，其荷载作用在圆柱圆心上，圆柱与平面只有一个接触面。而气囊搬运时，气囊上下均受到挤压，即存在两个接触面，但从式（6）可以看出，气囊搬运时的牵引力不是以单个接触面推导的滚动阻力系数成两倍关系。

1.3 滚动阻力系数的理论计算

以重35500 kN的圆筒出运为例计算滚动阻力系数。施工中气囊有效接触总长度L为126.8 m，气囊标称直径D为1.0 m，忽略气囊工作时的变形，半径R取0.5 m，囊体材料的弹性模量E1=0.66 MPa，泊松比v1=0.49，将以上数值代入式（2），（1-v2）/E2一项忽略不计，a值的计算式如下：

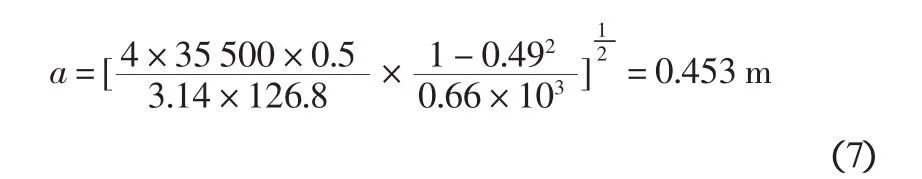
将式（7）代入式（3）计算λ值，有：

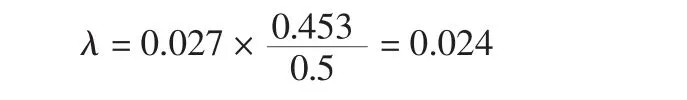
将λ=0.024代入式（6），可算得该圆筒气囊出运时的滚动阻力。

2 构件搬运时的牵引力测试

根据广西钦州港3个码头项目圆筒规格及气囊的数据，运用上述公式计算了滚动阻力系数及牵引力，结果见表1。表中Pe为气囊承受构件重量时的工作压力。

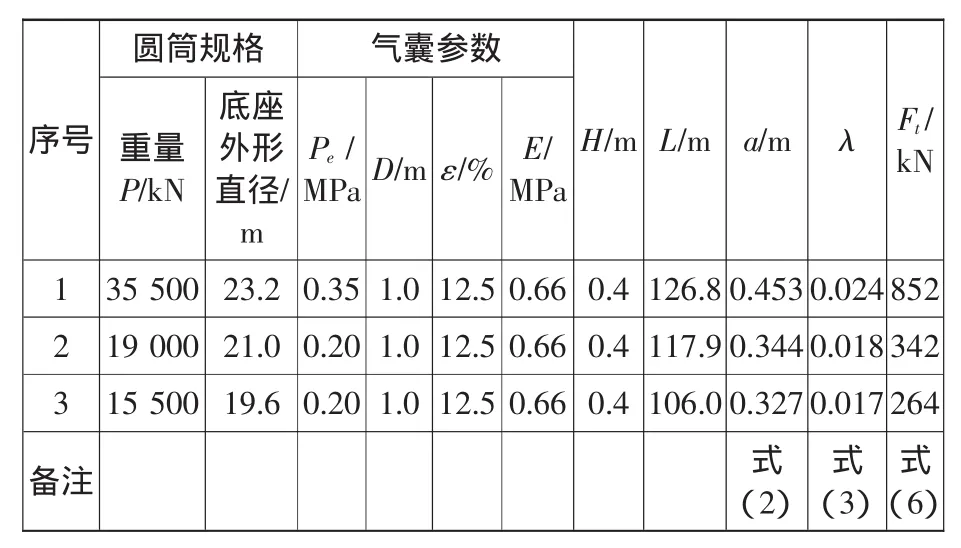
表1 圆筒气囊搬运的滚动阻力系数及牵引力计算

为验证按上述理论公式计算的滚动阻力系数是否合理，并判断以往凭经验估算的滚动阻力系数而选择的机具是否存在安全隐患或浪费，公司技术部门结合3个码头项目在气囊搬运施工过程中进行了牵引力测试并分析。测试采用两台100 t测力计（试验机准确等级：1级），检测器具布置见图3。

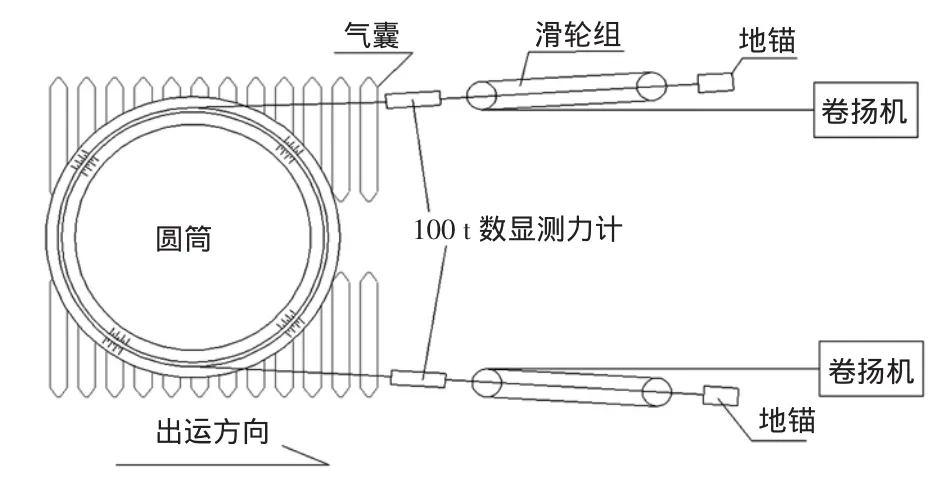
图3 牵引力测试布置图

为便于气囊搬运及浮游安装，在圆筒预制时加设了钢筋混凝土临时底板，以保证圆筒与气囊有充分的接触面积，圆筒安装完成后将临时底板与圆筒间的联接螺栓拆除。

2.1 搬运工作要点

本次测试，分别在水平面上及斜坡道上进行。搬运前进行圆筒底部气囊摆放工作，保证每个气囊的轴线与移运方向垂直，摆放完成后，对气囊进行充气，顶升圆筒至0.4 m的工作高度，检查每条气囊充气压力确保在（0.9～1.1）Pe的范围内，抽取支垫后准备前移时，再次检查气囊气压是否正常。各项准备工作无误后，开启测力计显示器、启动牵引卷扬机组、拉紧牵引钢丝绳，开始观察检测数据，前进中喂每一组气囊时，圆筒均有从静止到开始移动再到静止的一个过程，在此期间当观测数由递增改变为递减时，记录递减前一个数据。前进过程中保持溜尾钢丝绳跟进，不能与牵引钢丝绳抗衡。

2.2 牵引力测试结果

水平面移动时的牵引力测试结果见表2，表中实测牵引力F°值为两侧测力计测量值之和，平均值为全部F°值的算术平均值，λ°为实测牵引力F°值除以圆筒重量的商。

表2 总牵引力测试结果表

2.3 后溜力的测试结果

本试验只对重19000 kN的圆筒在斜坡段下行时进行了后溜拉力测试。出运斜坡道总长66.9 m，坡比为3.5%，在斜坡段上，不需要施加牵引力圆筒能自行下行。以气囊与重件为受力研究对象，圆筒在斜坡道上的受力分析见图2，圆筒重量可分解成Fx及Fy，坡比为3.5%时可计算得Fy=18980 kN，Fx=665 kN。根据平衡方程∑Fx=0，有：

后溜拉力的理论计算及实测值见表3，表中的λ值取表1中的计算值。

表3 斜坡段圆筒下行时后溜力理论计算与实测值

2.4 测试结果分析

1）对比表2的数据，测试结果的最大滚动阻力系数不超过理论计算，在施工中是按出现最不利的工况进行控制，因此具有较大的参考意义。由于圆筒在平移过程中各气囊受压的长度是变化的，故各气囊的工作压力是变化的，为减少充气和排气的工作时间，一般允许气囊压力变化范围在0.9～1.1Pe内，且理论计算时参照充气轮胎性能选取的弹性模量等不能真实代表气囊的性能参数，故测试结果的滚动阻力系数平均值与计算值有一定差异。

2）理论计算的刚体平面与实测预制场地坪存在差异，实际施工中的地坪局部存在散砂等杂物，对滚动阻力有一定影响，但测试结果不能反映影响程度。

3）测试结果显示气囊的滚动阻力系数不是一个常数。根据式（3），理论公式中的接触宽度2a为变量，它与气囊囊体材料的弹性模量、气囊的直径及每米承受的荷载有关，说明接触宽度2a不等于由几何关系推算式（9）中的B计算值，因为当气囊直径D、顶升高度H一定时，B为定值，若2a=B即λ为定值，与出运构件的重量无关，这显然与测试结果不符。

4）重19000 kN的圆筒在3.5%坡比的斜坡道下行时，若滚动阻力系数按常规取0.035，即摩阻力Ff=664 kN，据式（8），后溜拉力T趋于0 kN，显然与表3的实测结果不符，滚动阻力系数按常规取值在斜坡段下行时存在极大的安全隐患。

5）经测试，按式（3）计算的气囊的滚动阻力系数能满足实际施工要求。

3 结语

气囊搬运重件施工工艺因投资少、施工简便等优点，已在码头工程的重件搬运施工中普遍使用，经过3个项目构件搬运的牵引力测试，说明在编制构件出运施工方案时按经验选用的滚动阻力系数0.03～0.05明显偏大，一方面在水平面进行重件搬动时造成牵引钢索和牵引设备的浪费，另一方面在斜坡道下行时，由于滚动阻力实际偏小而下滑力偏大造成溜尾钢索安全系数不足，存在安全隐患甚至造成事故。

搬运气囊生产执行的标准CB/T 3795—1996《船舶上排、下排用气囊》中，没有要求在产品生产中进行弹性模量及滞后损失系数的测定，本文在进行理论计算时参考了汽车充气轮胎的相关数据，结合测试结果，可以知道气囊搬运构件的滚动阻力系数不是常数，工作高度一定时，它随着气囊承受的线荷载增大而增大。

当搬运码头与预制场间需设置斜坡道时，采用气囊搬运重件施工工艺的建议坡比不大于2%，以减小下滑力，确保安全。

本文只是对3种规格的圆筒采用气囊搬运工艺时进行了阻力测试和分析，结果可能存在偏差，期望通过更多构件的测试，进一步完善气囊滚动阻力系数的取值方法，更利于施工。

[1]HAILING J.摩擦学原理[M].上海交通大学摩擦学考研室译.北京：机械工业出版社，1980：166-171.

[2]庄继德.现代汽车轮胎技术[M].北京：北京理工大学出版社，2001：154-155.

[3]CB/T 3795—1996，船舶上排、下排用气囊[S].北京：中国标准出版社，1998.

[4]钱伟长，叶开沅.弹性力学[M].北京：科学出版社，1956：8-9.