内河船舶吨位丈量计算公式方法的讨论
2012-06-30周社宁褚卫明
周社宁,褚卫明
(江苏省船舶检验局,江苏 南京 210004)
0 引言
《内河船舶法定检验技术规则》(2011)(简称“法规”)已于2011年9月1日开始实施,其中第3篇“吨位丈量”中对新造及有资料船舶计算量吨甲板下围蔽处所容积V1做了较大的调整:将公式法改为容积计算方法。这一调整牵涉设计、审图、检验和海事管理等诸多方面,特别对一些已按公式法习惯性做法或对此有既定管理规定(或软件)的单位的船舶吨位计算工作影响较大,引起了不少争议和讨论。本文对公式法的由来及原理进行了介绍,分析了公式法存在的缺陷,从而得出用容积法代替公式法是必然趋势。
1 公式法的由来及原理
1.1 公式法的由来
1959年我国参考英国、前苏联等国吨位丈量规则,以辛氏法作为基本点的“摩逊法”为基础,制定了建国后的第1个《船舶吨位丈量规范》,适用于海船兼作河船参考,其内容比较简单。1978年我国制定了第2个《船舶吨位丈量规范(国内航行船舶部分)》(试行本),主要规定了包括辛氏法在内的3种容积丈量计算方法,其内容与1959年规范基本相同,只是要求更加详细,增加了插图和对船体凸出体的丈量方法,其适用范围是海船河船通用。1986年我国发布了第一个明确为内河船适用的《内河船舶吨位丈量规范》,直至1999年、2004年、2011年的法规都将内河船舶吨位丈量与海船分开,单独实施其计算方法。由于船舶吨位丈量历来都有多种计算方法,比较繁琐,根据当时我国内河船舶船型小、船型简单、船舶吨位的社会作用不显著、不敏感的特点以及计算机技术的落后,为简化计算的工作量和避免结果的不一致,1986年的内河丈量规范统一采用了公式法的计算方法。该法相对于繁杂的手工计算而言比较简单,结果相对准确,而且通常情况下对新造及现有资料船舶计算量吨甲板下围蔽处所容积V1只允许使用此法。1986年至2011年一直沿用的公式法如下:
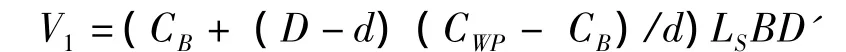
式中:d为设计满载吃水;CB为设计满载吃水时的方形系数;CWP为设计满载吃水时的水线面系数;LS为设计满载吃水时的水线长;B为型宽;D为型深;D′为修正型深,D′=D+h/2+(hS+hW)/6,其中:h为梁拱高;hS为船首舷弧高度;hW为船尾舷弧高度。
1.2 公式法的原理
1986年以前吨位丈量计算均采用排水体积式的容积曲线或邦氏曲线或辛氏法等方法求得V1的数值,而公式法则是采用了若干个相关船舶参数,通过这些参数的推算来求得V1的数值。公式法主要是使用CB值在静水力曲线的外插及近似判断和一定量船舶的统计数据分析的方法:公式中的D'取值为修正型深,这与排水体积的曲线计算方法无异;根据船舶参数的定义,公式中的V1也就是在D'下的型容积,(CB+(D-d)(CWP-CB)/d)就是在D'下的方型系数CB',而(D-d)(CWP- CB)/d就是对CB外插的修正值。
推导该公式的过程中,根据内河船舶特点,作了如下3个假设:
(1)设计水线以上水线宽保持不变,是个常数。
(2)水线面系数与吃水为线性关系,且在设计吃水一半时,水线面系数等于体积平均系数即方形系数。
(3)干舷不是特别高(1 m以内)。
公式中型深D'的修正计算含了梁拱和舷弧的影响,分别介绍如下:
(1)梁拱的影响
梁拱对主船体容积的影响,可以考虑为型深在原来基础上的一个增加,如将梁拱线看成一直线,即原型深以上是三角形。根据等面积原理,与该三角形面积相等的矩形高应为梁拱高度的一半,即相当型深为:D′=D+h/2,此为2004法规中梁拱等效。如将梁拱线看成是一个弓形,根据等面积原理,与该三角形面积相等的矩形高应为梁拱高度的2/3,即相当型深为:D′=D+2h/3,此即为2011法规中梁拱等效。
(2)舷弧的影响
舷弧对主船体容积的影响与梁拱类似,但假定舷弧线看成是一抛物线,首舷弧的面积在前半体的等效高度为hS/3,综合到全船范围即hS/6,尾舷弧类似,相当型深为:D′=D+hS/6+hW/6
综合梁拱、舷弧的影响为:

2 公式法的缺陷
(1)从上述推导公式看到,公式法是利用了CB与CWP随吃水变化规律相似的特性,设置了一些假定,如设计水线以上水线宽保持不变或水线面系数与吃水为线性关系等,但实际上对绝大多数船舶而言这是不可能的。公式是在汇总了当时内河主流船型的基础上统计得出的,忽略了它们的差异,因此不能以这些假设为前提的公式来涵盖所有内河船舶。另外,为达到使假设或相似关系的成立及公式的简化,在式中既有D的采用又有D′的引用,还有与这D与D′均无关的LS的引用,显得比较混乱。这种D与D′位置差异及与LS的混用,对修正值CB′的准确确定无疑也是有影响的。
(2)从公式法中看出,CB的修正值(D-d)·(CWP-CB)/d中(D-d)/d愈大,则修正愈大,D的位置在d的外插位置,从数学上知道曲线斜率不等的情况下,外插点越远外插的结果误差越大。(D-d)/d表示的是干舷与吃水的比值,因此相对讲船舶吃水愈浅,(D-d)/d就越大,外插误差就越大,这就说公式法对浅吃水船吨位丈量计算产生的误差大。而浅吃水船是内河中的典型船型,在内河船舶数量中占有相当的比例,使得公式法在浅吃水船中使用有很大的局限。
(3)从公式法中看出,(CWP-CB)值愈大,则修正值也愈大。对某一船来讲由于船舶三维外型特性,(CWP-CB)值愈大或随着吃水增加呈增长趋势,则船舶外飘(包括侧飘和前后飘)愈大,对这类船的吨位丈量计算产生的误差一定也愈大。内河的客船、甲板货船和一些其他船舶为追求较大的甲板面积,都存在着不同程度的外飘,有的还相当大,因此这类船使用公式法也有很大的局限。
(4)从公式法中看出,当时为使用简便,对船舶附体和突出物的容积没有考虑。随着内河船型的大型化和复杂化,船舶带有附体和突出物的现象愈来愈多,也使得公式法在使用中造成结果误差增大。
在船舶吨位越来越受到社会关注的情况下,公式法的上述缺陷在使用过程中,对有些船的影响是单一的,对有些船是交织的,有些还是比较严重并且难以通过其他方法纠正或解决的缺陷。由于这些缺陷的综合影响及不确定的作用,决定了其带来的弊端还是较严重的。
如某1200客位渡船主要量度为:

用公式法得到的V1=1009.6 m3;而用容积曲线方法得到的 V1=1107.5 m3,两者相差 97.9 m3,换算成总吨,相差29。
某70 m散货船主要量度为:

用公式法得到的V1=4938 m3;而用容积曲线方法得到的V1=4810 m3,两者相差128 m3,换算成总吨,相差38。
3 公式法沿用与否的分析
从上述情况得知,1985年至2011年间内河船舶吨位丈量规范中对新造及现有资料船舶计算量吨甲板下围蔽处所容积V1仅允许使用公式法显然已不适宜,尤其在计算机和船舶软件不断发展的今天。通过计算机采用容积曲线方式进行吨位计算丈量,使得公式法已没有任何优势可言,特别是准确性方面更不如计算机计算结果精确。据不完全统计,采用公式法比容积曲线方法计算得到的V1结果平均误差约在5%以内,折算成总吨的误差在1% ~3%以内,因此不少人对公式法沿用与否产生了不同意见,包括新法规评审时也有争议。其主要观点为:
(1)有人提出既然公式法已沿用了20多年,经其丈量的船舶吨位也已经既成事实,况且吨位丈量仅是人为的约定行为,作为唯一的公式对同一种船型来讲结果是公平的也是唯一的。
作者认为既然已经证明公式法存在缺陷,且这些缺陷不仅对船舶的共有属性和总的公平带来了影响,还对如设备配置、船员配备等产生延伸影响,特别是对一些临界吨位的船舶的影响。问题越积越多,情况愈加复杂。与其长痛不如短痛,况且法规对现有船舶的吨位不做强制追溯;同时国际上通行的吨位丈量公约或规则的计算以及我国海船吨位丈量计算都是采用容积曲线或辛氏法,内河船舶在这方面没必要作特殊的对待。
(2)有人提出公式法和容积曲线法能否共存,作为过渡期同时允许使用。
从上述的2个例子可以证明,2种方法假如同时使用,由于计算结果的差异,如果船东、设计单位或管理部门各取所需,将会给船舶吨位丈量工作带来混乱,甚至成为社会问题。新法规在合理考虑过渡问题时已经注意到这个方面,即对无资料的现有船舶其主体部分和附加部分仍然允许采用公式法。由于目前这种无资料的现有船舶现象已很少,新法规这样的方式既考虑到了以往的现实与过渡,也不会对今后新造船产生冲击,是一种较宜的处理方法。
4 结语
用容积曲线方法或辛氏法代替公式法的趋势是不言而喻的,《内河船舶法定检验技术规则》(2011)的这一调整是必要的,调整利大于弊,对此应该有一个明确的认识:公式法不能再应用于新造及现有资料船舶计算量吨甲板下围蔽处所容积V1。至于对新内河法规中有关哪些项目是否应该计入吨位丈量的争论,从而会引起我国内河船与海船、尤其与国际上的一些通常计入项目和其计算结果的偏差的问题,随着时间的推移,大家也会有一个共识的。
