利用Trimble Geomatics Office实现坐标转换方法的探讨
2012-06-29于亚杰
于亚杰
(河北省第二测绘院,河北石家庄 050031)
1 引言
随GPS产品应用范围的拓宽、技术的发展和成熟,GPS数据处理软件业随之发展和完善。Trimble公司研发的TGO(Trimble Geomatics Office)软件是大家较为熟知的一款随机应用软件,它可以处理所有Trimble GPS的原始测量数据和其他品牌的GPS数据(RINEX),整个软件包由多个模块构成,并具有专业的数据处理报告。TGO软件功能强大、自动化程度高、结果可靠,在坐标转换、参数求取中具有很强的功能,且操作方便。
2 不同地球椭球坐标系的空间七参数转换
不同椭球体间的坐标转换(局部地区)采用的最多的方法是布尔沙模型,也就是七参数的相似变换法,即3个平移参数(△X0△Y0△Z0)T、3个旋转参数(ωXωYωZ)和1个尺度参数m,七参数转换数学模型如图1所示:

图1 七参数转换示意
由空间直角坐标系A到空间直角坐标系B的转换关系为:
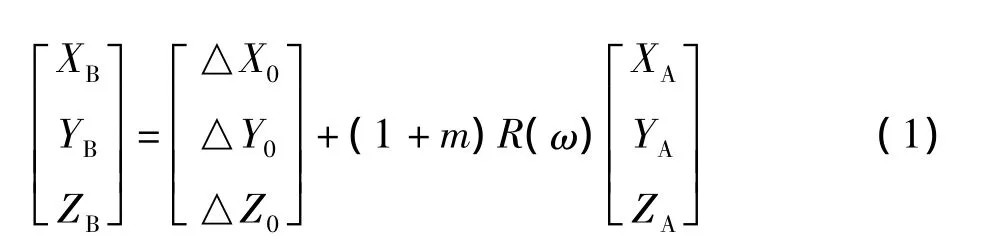
(XAYAZA)T为某点在空间直角坐标系A中的坐标;
(XBYBZB)T为该点在空间直角坐标系B中的坐标;
(ωXωYωZ)为空间直角坐标系A转换到空间直角坐标系B的旋转参数;
(△X0△Y0△Z0)T为空间直角坐标系A转换到空间直角坐标系B的平移参数;
m为空间直角坐标系A转换到空间直角坐标系B的尺度参数。

七参数若不考虑尺度参数,称为六参数转换模型,若仅考虑3个坐标平移参数,则称为三参数转换模型。如果区域范围不大,最远点间的距离不大于30 km,一般可以采用三参数。转换参数的求取方法通常是获得控制点无约束平差下的WGS-84坐标,同时将已知的地方坐标化为空间直角坐标形式,由(1)式,按最小二乘求出转换参数。如某测区内有若干控制点,有经自由网平差得到WGS-84坐标成果及1954年北京坐标系(中央子午线为117°、3°带)平面直角坐标成果,现需求取一套七参数,以便将参数输入到RTK电子手簿中,进行外业采集。
首先在TGO软件坐标管理器中新建坐标系统BJ-117。新建任务,在默认的坐标系统下将控制点的WGS-84坐标成果导入,其次将坐标系统改变为BJ-117,选择测量下拉菜单里的点校正,选择基准转换中的七参数,打开点列表,依次输入控制点的平面直角坐标及高程成果,点水平平差、垂直平差,然后点计算。
水平平差归算出控制坐标与由GPS定位值计算出的格网坐标之间的残差;垂直平差是由确定原点的垂直位移和北/东方向上的高程面倾斜度组成的倾斜调整。根据校正出来的几个参数可以大致判断是否有错误发生。一般地,平差比例尺在1左右,可能是0.9999…或者1.0000…。控制点不能覆盖足够大的区域时,很容易求出不太精确的参数计算值来做转换,一般来说,除了控制点覆盖的范围大约为 80 km×80 km的情况,其他都不应该计算七参数转换,还要注意的是计算出的旋转值不应超过10″[1]。打开报告查看七参数结果,如图2所示:

图2 报告中的七参数
较其他软件相比,TGO可批量导入坐标文件进行参数求取,界面直观,且在发现残差过大时调整操作方便,提高了工作效率。
采用七参数空间转换模型时,需要将地方坐标系转换为其参考椭球下的空间直角坐标,而在我国平面坐标与高程系统分离,以本文为例,就无法获得准确的北京54坐标参考椭球的大地高,只是用水准高程代替。不过,有关专家对大地高误差对转换参数的影响进行了分析,证明了对于地面上小于100 km×100 km的范围,即使公共点的高程存在误差,转换出来点的平面坐标仍基本不变[4]。
3 不同平面直角坐标系坐标转换四参数计算
平面坐标的转换,如国家坐标系到地方独立坐标系或两种地方独立坐标系间的转换,通常通过公共点来求取参数。方法有:正形多项式变换模型(八参数)、仿射变换模型(六参数)、相似变换模型(四参数)。通常采用四参数法,即两个平移因子、一个旋转因子和一个尺度因子,方法又包括两种:
(1)先旋转、再平移、最后统一尺度

(2)先平移、再旋转、最后统一尺度

四参数的控制范围通常为20 km2~30 km2。TGO提供四参数转换,即根据至少3个公共点在两个坐标系中的坐标应用最小二乘法原理求得,采用的方法是式(3),过程如下:首先新建项目,坐标系统为默认,导入地方坐标系成果,如:[点名],[北坐标],[东坐标](也可插入点,但是坐标属性不能为控制质量),其次选择测量→坐标转换→点列表,依此点取公共点,并输入其新坐标值,如图3所示。
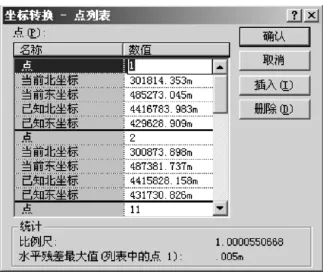
图3 点列表界面
建立转换报告查看计算的四参数:

图4 四参数报告
笔者采用了由武汉大学测绘学院研发的Cosa GPS数据处理软件对同一组数据进行了四参数坐标转换,两套软件计算的比较结果如表1所示。

利用COSA与TGO采用四参数计算成果表 表1
通过将TGO与国内权威软件的计算结果比较可知,TGO此项功能计算出的结果完全满足精度要求。
4 坐标投影面变换
TGO软件可以通过椭球膨胀法和椭球平移法来实现指定高程面上的平面坐标转换。椭球膨胀法较复杂,由于篇幅有限,本文只介绍椭球平移法。椭球平移法的基本思想是指独立坐标系参考椭球的长半轴、扁率与国家坐标系参考椭球一致,只是将国家坐标系参考椭球沿测区的项目位置点的法线方向平移H(大地高),使椭球面与该点相切,将坐标转换到该参考椭球的坐标参照系下,再对这些坐标进行投影变换,得出在指定高程面上的平面坐标。这样位置基准点的经纬度不变,但椭球中心平移使得点的三维坐标发生变化,如图5所示。
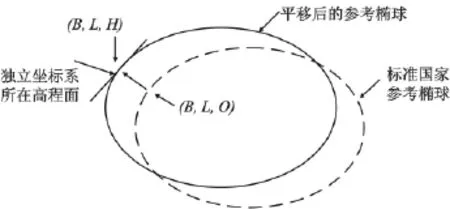
图5 椭球平移法示意图
算例:某一测区平均纬度为40°47',平均大地高面200 m。测区内原控制点坐标系统为1980西安坐标系(117°中央子午线、3°分带)平面直角坐标。现保持椭球及中央子午线不变,将投影面抬高至200 m平均大地高面建立地方独立坐标系。实现过程如下:新建坐标系统XIAN80-117。新建项目,将项目属性中的坐标系统由默认改为XIANN80-117,选择当地点设置→改变→选择当地,纬度输入测区的平均纬度(建立独立坐标系时可选择测区中间一点的纬度输入),经度输入中央子午线值117°,高度输入200(为投影面高度),然后选择使用地面坐标→用投影位置比例尺计算→确认→应用,然后导入1980西安坐标系参考椭球下的平面直角坐标或是的大地坐标(也可直接采用国家坐标系成果二维约束后的控制网数据),导出平面坐标,完成转换,如图6所示。
需要说明的是,此种转换方法与椭球膨胀法在北坐标偏差上会存在一差值,可在上图北坐标偏差中输入差值,减少差异。
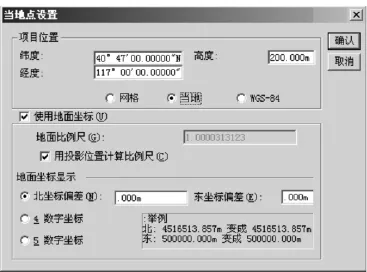
图6 当地点设置
5 高斯正反算及换带计算
先在坐标系统管理器中建立两个坐标系统:XIAN80 -117、XIAN80 -117.30。
高斯正算:新建项目→坐标系统→改为XIAN80-117,导入基于该坐标系统下的大地坐标数据,进而导出该投影带下的平面直角坐标。
高斯反算:新建项目→坐标系统→改为XIAN80-117,导入该投影带的平面直角坐标,然后导出基于该参考椭球下的大地坐标。
换带计算:新建项目→坐标系统→改为XIAN80-117,导入XIAN80-117的平面直角坐标,在项目属性中改变坐标系统为XIAN80-117.30,然后导出的平面直角坐标,完成转换。
6 结语
(1)基准转换要求很高的坐标精度和准确度,因为每一种坐标基准都有着严密的椭球参数定义。选择了用于球转换参数的控制点之后,用户必须为它们准备相当准确的WGS-84坐标和地方椭球坐标。
(2)点校正最大的功能是当地方独立坐标系参考椭球未知时,可以用点校正功能解决实际问题。其次也可以求解出局部的WGS-84至地方直角坐标系七参数(或三参数),但无法求解出北京54坐标与西安80坐标系下近似正确的平面坐标成果转换参数。四参数只能转换平面坐标,在进行四参数计算时,源坐标可以为WGS-84坐标系下平面直角坐标,有时直接把WGS-84的大地坐标当作北京54的大地坐标(或者西安80坐标,肯定会存在偏差),经过投影后再通过四参数转换成施工坐标平面坐标,最后通过高程拟合参数转换高程。
(3)通过TGO项目属性的当地点设置,可以很好的解决投影面坐标转换问题,而且方便根据控制网中心一点的平面坐标和测区平均高程数据建立独立坐标系统。
[1]李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2007.
[2]CJJ8-99.城市测量规范[S].
[3]施一民.现代大地控制测量[M].北京:测绘出版社,2003.
[4]王解先,邱杨媛.高程误差对七参数转换的影响[J].大地测量与地球动力学,2007(3).
