基于失真-量化模型的视频编码算法优化
2012-06-26郭龙盛殷海兵
郭龙盛,殷海兵,徐 宁
(中国计量学院信息工程学院,浙江 杭州 310018)
随着视频技术的发展,一系列的视频编码标准相继出现,H.264/AVC是目前最成熟的视频编码标准。在视频编码过程中,码率控制和模式选择已经成为一个研究热点。码率控制即通过R-D模型来选择量化参数,分配编码比特。R-D模型通常包括R-Q模型和D-Q模型,本文主要对D-Q模型进行深入研究。
近几年来,一些学者专家基于DCT系数分布模型提出了许多D-Q模型。文献[1]基于柯西分布提出D-Q模型;文献[2-3]提出一种基于拉普拉斯分布的D-Q模型;文献[4]提出一种基于广义高斯分布的D-Q模型,文献[5]对基于柯西的D-Q模型进行了改进,文献[6]基于这些失真模型总结了其在率失真模型中的应用。面对这些主流的D-Q模型,有必要对其进行精确度和复杂度的比较,分析其优缺点,目的是在此基础上对D-Q模型加以改进。
1 主流的D-Q模型
本节将简单介绍目前几种主流的D-Q模型,包括基于拉普拉斯分布、柯西分布、广义高斯分布的D-Q模型。
1.1 基于拉普拉斯分布的D-Q模型
文献[2]中基于拉普拉斯分布提出了估计编码失真的方法,公式为

式中:β是一个模型参数;p与编码帧类型有关。
1.2 基于柯西分布的R-Q模型
文献[1]根据柯西分布概率密度函数,通过理论推导简化了D-Q模型

式中,参数b与编码帧熵值有关。
1.3 其他主流D-Q模型
文献[7]根据QP和PSNR的关系推导出了一个新的D-Q模型

赵欣等人在文献[4]中提出了一个新的D-Q模型

2 D-Q模型精确度分析
2.1 帧级D-Q模型精确度比较
本节通过实验对上述4种D-Q模型帧级精准度进行分析。Model SATD,Model Cauchy,Model MSW,Model GGD分别代表上节中公式(1)(2)(3)(4)的模型。由于篇幅限制,只给出了对Foreman和Bus序列的测试(笔者已经证实对其他序列的测试也有相同结果),如图1所示。
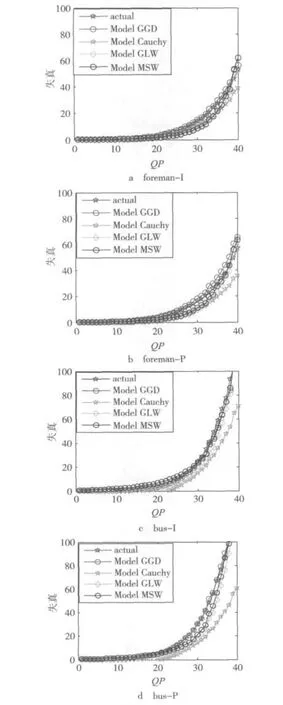
图1 帧级D-Q模型精确度的比较
由图可见,Model GGD可以较好地估计出实际失真,但复杂度也是最高的,对于硬件实现是一个比较大的挑战。从上节中的4个公式也可发现,Model Cauchy的复杂度是最低的。
2.2 宏块级D-Q模型精确度比较
由于宏块级的D-Q模型对码率控制和模式选择而言非常重要,因此有必要对宏块级的D-Q模型进行研究,为了比较宏块级D-Q模型的精确度,笔者做了大量实验。如图2所示,横坐标表示用模型估计出的失真和实际失真的差值(error),纵坐标表示宏块的数目(nMB),在横坐标为0附近的时候,纵坐标的值越高,说明了该模型的精确度越高。该实验的测试环境是foreman和football序列,QP值为36。可见,在foreman序列中,基于柯西分布的D-Q模型精确度是最高的;在football序列中,Model Cauchy的精确度要略低于其他D-Q模型,但其复杂度最低。

图2 宏块级D-Q模型精确度的比较
3 改进后的D-Q模型
在对几种主流D-Q模型的精确度进行比较之后,下面将对基于柯西分布的D-Q模型加以改进,以提高其精确度。
如式(2)所示,基于柯西分布的D-Q模型中有两个参数——b和β,它的参数更新是根据前一帧相同位置块的实际失真来计算当前块的参数。众所周知,相邻帧里的宏块由于运动会发生位移,直接采用前一帧相同位置的宏块来计算当前参数会产生误差,因此,本文提出了一种基于运动补偿的D-Q模型,即通过补偿后的参考帧来预测当前块的模型参数。结果如图3所示,横坐标表示宏块实际失真和模型估计得出的失真的差值,纵坐标表示宏块个数,本实验的测试序列是foreman序列,图3a和图3c是原始柯西模型的结果,图3b和图3d是改进后模型的结果,可见改进后的模型明显要比原始模型的精确度要高。为了更加清楚地对这两个模型精确度进行比较,在表1中列出不同序列、不同QP下计算得到

式中:distortion_a(i)和distortion_a(i)分别代表实际失真和模型估计的失真。

图3 改进后的模型和原始D-Q模型精确度的比较

表1 原始柯西模型和改进后模型error_rate的比较
4 结论
本文介绍了目前主流的几种D-Q模型,并且从宏块级和帧级进行了精确度的比较,在宏块级中,针对不同的序列,各模型有不同的性能,当视频运动信息比较少的时候,基于柯西分布的D-Q模型精确度较高,当视频运动比较复杂的时候,赵欣等人提出的模型精确度较高;在帧级中,公式(4)中的模型精确度较高。然后在基于柯西分布的D-Q模型基础上加以改进,提高了模型精确度。
由于D-Q模型的复杂度和数据依赖关系,在硬件中实现是一个较大的挑战。在以后的工作中,将重点研究适用于硬件实现的D-Q模型。
[1]KAMACI N,ALTUNBASAK Y,MERSEREAU R M.Frame bit allocation for the H.264/AVC video coder via cauchy-density-based rate and distortion models[J].IEEE Trans.Circuits Syst.Video Technol.,2005,15(8):994-1006.
[2]KWON D-K,SHEN Mei-yin,KUO C-C J.Rate control for H.264 video with enhanced rate and distortion models[J].IEEE Trans.Circuits Syst.Video Technol.,2007,17(5):517-529.
[3]GUO Liwei.A novel analytic quantization-distortion model for hybrid video coding[J].IEEE Trans.Circuits Syst.Video Technol.,2009,19(5):627-641.
[4]ZHAO Xin,SUN Jun,MA Siwei,et al.Novel statistical modeling,analysis and implementation of rate-distortion estimation for H.264/AVC coders[J].IEEE Trans.Circuits Syst.Video Technol.,2010,20(5):647-660.
[5]HU Sudeng,WANG Hanli,KWONG S,et al.Rate control optimization for temporal-layer scalable video coding[J].IEEE Trans.Circuits Syst.Video Technol.,2011,21(8):1152-1162.
[6]马宏兴,张伶.H.264/AVC率失真优化技术综述[J].电视技术,2010,34(6):19-22.
[7]MA Siwei,GAO Wen,LU Yan.Rate-distortion analysis for H.264/AVC video coding and its application to rate control[J].IEEE Trans.Circuits Syst.Video Technol.,2005,15(12):1533-1544.
