R500B离心机振动台动力试验性能分析

李京爽，侯瑜京，徐泽平，梁建辉，张雪东，宋献慧

(中国水利水电科学研究院岩土所，北京 100048)

1 研究简述

中国水利水电科学研究院450 g-t土工离心机［1］配置的 R500B 电液伺服振动台［2－3］，是国内首台能够实现在水平和竖直双向控制振动的离心机振动台，其主要技术指标见表1。为进一步了解该振动台的性能，设计并完成了一系列动力离心模拟试验，这里主要介绍通过这些试验反映的振动台的动力性能和特点。

表1 R500B振动台主要技术参数Table 1 Technical parameters of R500B

地震模拟振动台试验是结构工程、水利工程常用的研究模型动力性能的一种试验方法。大型地震模拟振动台试验在结构工程中应用较为广泛，但对大坝等水工结构来说，重力引起的非线性材料内部应力的作用十分明显，必须予以考虑。因此离心机中的地震模拟振动台试验，也得到了重视和发展。

离心机中的地震模拟振动台与一般大型地震模拟振动台有明显不同:

(1)借助离心机模拟重力场的优势，考虑了模型的应力约束效应。通过离心机使模型置于Ng(N为模拟重力场加速度与地面重力加速度g的比值)的模拟重力场中，而模型的几何尺寸取为原型的1/N，从而模型和原型结构的内部应力相等;

(2)工作频率较宽。一般地震频率为0.1～10 Hz，地面上振动台的工作频率满足此要求即可。而离心机中振动台因为考虑了模型几何缩尺效应，其频率响应增大N倍，故振动频率最大可到400 Hz以上，因此对机械性能要求较高;

(3)地震时间响应缩减为原型地震的1/N。可见，除了应用离心机模拟重力场这个特点外，为了得到目标地震响应，地震模拟振动台不可直接采用原型地震波作为激励波，而应采用相应处理后的波形作为激励波形。

地震模拟振动台是一个复杂的机械系统，不可能达到输入即为输出，其输出波和输入之间必然存在差异。一般可在时域和频域2个方面分析其差异。相干函数是频域上描述系统输入输出相关程度的实值函数，又称为凝聚函数，相当于时域中的相关分析。记输入和输出信号分别为x(t)和y(t)，其相干函数特点如下［4］:

(1)对于一个线性时不变系统，在无噪输入和输出的理想情况下，其相干函数必然等于1，即

(2)若 x(t)，y(t)完全不相关，即 Gxy=0，则=0;实际测试中相干函数在0～1之间。

广义来说，相干函数是度量任意2个量和信号的因果程度的实值函数，在振动、交通等领域应用较广，也有作者用来作为离心机中振动台的性能指标［5］。一般认为相干函数达到0.7 ～0.8以上时，振动系统控制性能较好。下文分析已有试验数据的相干性来说明中国水利水电科学研究院最新研制的R500B大型离心机振动台的动力性能，同时也以120 Hz正弦波为例，说明其对正弦波的模拟能力。

2 地震波激振

R500B台面上模型和模型箱质量共443 kg，试验离心加速度为30 g。采用平潭标准砂自由场地基模型进行动力模型试验［6］，振动台输入地震波，如图1所示，其时长为1.0 s，加速度峰值约200 m/s2，频率范围90～350 Hz。振动顺序为水平单向、竖直单向和水平竖向双向振动，图2至图4为在30 g离心加速度下各种振动工况下台面输入、输出波之间的相干分析。

图1 R500B地震模拟振动台激励地震波Fig.1 Excitation earthquake wave for R500B

2.1 水平激振

图2是水平方向激振时的相干函数。图2(a)表明，水平振动时，在给定的频率范围内，相干函数值达到0.9以上，对地震波的重现能力较好。虽然在个别频率有突降现象，但整体结果较好。在次振方向，相干函数应越小越好。图2(b)中，在给定的频段内，相干函数在个别频率有突升现象，但大部分图形在0.4以下，这说明次振受主振方向影响程度较小。

2.2 竖向激振

图2 在30 g离心加速度下水平激振时的相干性Fig.2 Coherence upon horizontal excitation at 30 g centrifugal acceleration

图3是竖向激振时的相干函数图形。图3(a)表明，在90～200 Hz之间，水平/主振方向相干函数值超过0.8，但有个别突降点，在此频率段内，对地震波的重现能力较好。在200～350 Hz之间，相干函数值降低较为明显，平均约为0.2。在水平/次振方向，如图3(b)示，在90～200 Hz之间，相干函数均值约为0.4，在200～350 Hz之间，相干函数均值在0.2以下，在单独输入垂直向地震波的情况下各频段内相干性略差。应该注意到振动台对地震波的重现能力与通过迭代确定传递函数有关。同一个波形，迭代次数多，传递函数能使输出波形更好重现输入波形，一般迭代2～3次即可。上图为迭代2次结果。但对较复杂波形，特别是双向激振，可能需要的叠加次数较多才能达到较好的效果。

图3 在30 g离心加速度下竖向激振时的相干性Fig.3 Coherence upon vertical excitation at 30 g centrifugal acceleration

2.3 双向激振

图4 在30 g离心加速度下双向激振时的相干性Fig.4 Coherence upon bi-axial excitation at 30 g centrifugal acceleration

在双向激振时的相干分析如图4(a)所示，有意思的是，2个方向的相干函数与单向分别激振时主振方向的相干函数相似，虽然也在个别频率有突降点。这是由于在2个方向的振动是分别由两个独立的液压作动器控制，因此出现上述现象。

2.4 较高离心加速度下相干分析

工程及科研通常也要求动力试验可以在较高离心加速度下进行。在高g值(50～80 g)离心加速度下，不仅振动台作动器要经受较大的考验，而且也对离心机转臂平衡有较高要求。在80 g离心加速度下的试验，离心机负荷已经接近其设计的额定性能。在我们进行的测试和相关试验中，已经较为成熟地采用50 g(含)以下离心加速度。这里提供2组50 g和80 g离心加速度下采用443 kg方形大铁块进行的测试试验结果，波形也采用图1所示地震波。

从图5可见，在50 g离心加速度下的单向分别激振时，水平方向的相干函数值在90～270 Hz范围内可达到0.8，竖向的相干函数值在90～200 Hz范围内也可以达到0.8。这要逊于30 g离心加速度下在水平方向的成绩，但要好于竖向的成绩。

图5 在50 g离心加速度下单向分别激振时的相干性Fig.5 Coherence upon separate excitation at 50 g centrifugal acceleration

从图6可以看出，在80 g离心加速度下，双向激振时，水平方向相干函数值在90～270 Hz范围内可达到0.8，竖向的相干函数值在100～240 Hz范围内也可以达到0.8。这和50 g离心加速度下的测试成绩相差不大。

图6 在80 g离心加速度下双向激振时的相干性Fig.6 Coherence upon bi-axial excitation at 80 g centrifugal acceleration

3 正弦波激振

对同一模型进行的试验中，采用了振动频率为120 Hz带上升、下降缓冲段的正弦波，其时域曲线见图7，波形时长0.6 s，前0.15 s和后0.15 s为上升和下降段，中间有0.3 s的持续段，其傅立叶变换在120 Hz处有一加速度峰值75 m/s2。

图7 激励正弦波Fig.7 Excitation sine waves

图8为水平单向激振时台面输出波形，为说明台面输出与输入之间的相近水平，可将其水平持续段放在图9中进行比较:输入波和输出波之间的吻合度非常好，其峰值较激励波稍大，有峰值之间有轻微波动;输出波比输入波延迟约0.003 s，约为1/3周期。频域图中可知，除 120Hz处有峰值外，在 2倍、3倍输入频率也有小峰值，并逐渐减小。这是由于振动输出并非完全的正弦振动，故有高阶谐波分量，这导致输出波形在120 Hz加速度峰值减小为70 m/s2。因高阶谐波是实际发生的振动，故不作滤波处理。

图8 水平激振时台面输出振动波形Fig.8 Output waveforms upon horizontal excitation

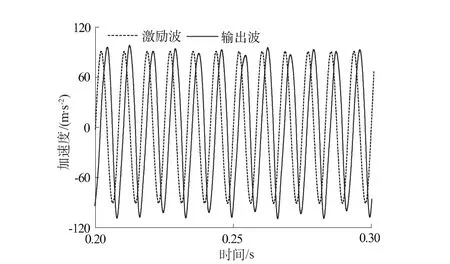
图9 正弦持续段激励和输入波形比较Fig.9 Comparison of exciting and excited waveforms for sine wave stable duration

振动台设计为在竖向平面内振动实现水平和竖向2个方向的振动，但其本身为三维机械结构，当某方向激振时，必然会引起在平面内另一方向的振动，也会引起垂直于此平面方向的振动。图10和图11是水平单向激振时引起的另外2个方向的振动，其中图11为竖向，即机械允许振动方向的振动，时域图上其最大峰值约为输入最大值的15%，应注意其频域图上也包含了些许均匀分布的机械噪声，导致域图上峰值点较多，看起来有点杂乱。图12为垂直振动平面方向的振动，时域图上其值与主振方向相比，不到2%，时域图上其最大峰值亦不超过1 m/s2。

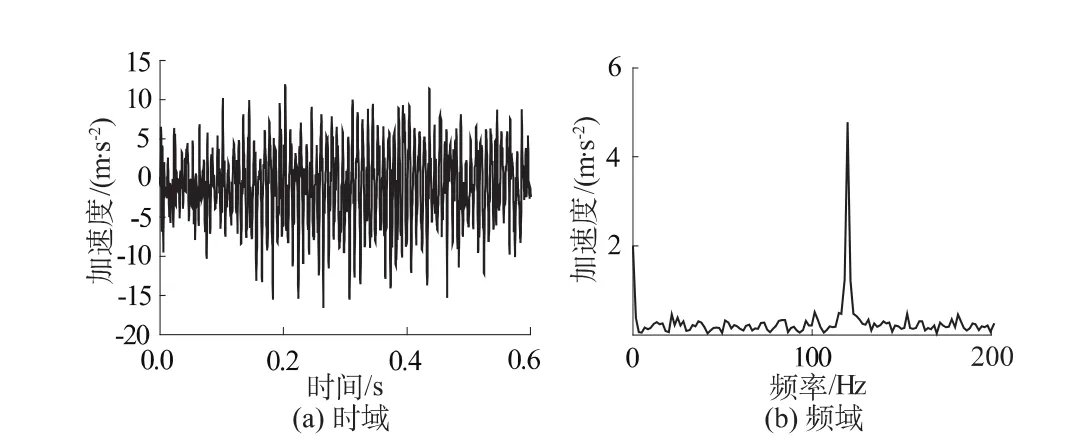
图10 水平激振时竖向方向波形Fig.10 Vertical waveforms upon horizontal excitation

图11 水平激振时垂直于振动平面的振动波形Fig.11 Output waveforms on the plane perpendicular to the shaking plane

4 结论

本文对一个复杂地震波在频域内做相干分析，并以120 Hz正弦波为例，介绍了振动台对地震波的重现能力。必须说明的是，以上测试和试验均在其工作负载达430 kg时进行。主要结论如下:

(1)在30 g的模拟重力加速度下，采用90～350 Hz的激振波，振动台水平方向的相干函数值可达0.9，竖向的相干函数值有所降低。

(2)在50 g和80 g离心加速度下，水平方向的相干函数值在90～270 Hz内可达0.8，竖向在100～200 Hz内可达0.8。

(3)双向激振时主振方向的相干函数与单向激振时主振方向相干函数基本一致。这也表明2个方向液压作动器可相互独立工作，互不干扰。

(4)在120 Hz正弦波的激振下，其主振方向输出波与输入波吻合度较好，次振方向加速度与主振方向相比分别为15%和不到2%。

以上测试分析结果表明R500B离心机振动台对复杂地震波和正弦波具有较好的重现能力，振动台动力性能优越。

［1］杜延龄，朱思哲，刘令瑶，等.LXJ－4－450土工离心模拟试验机的研制［J］.水利学报，1992，23(2):19－28.(DU Yan-ling，ZHU Si-zhe，LIU Ling-yao，et al.Development of LXJ－4－450 Centrifuge for Geotechnical Engineering［J］.Journal of Hydraulic Engineering，1992，23(2):19 －28.(in Chinese))

［2］侯瑜京.土工离心机振动台及其试验技术［J］.中国水利水电科学研究院学报，2006，4(1):15－21.(HOU Yu-jing.Centrifuge Shakes and Test Technique［J］.Journal of China Institute of Water Resources and Hydropower Research，2006，4(1):15－21.(in Chinese))

［3］HOU Y J，WANG X G，XU Z P，et al.Development of a Horizontal and Vertical Shaker for the IWHR 450 g-ton Centrifuge［C］∥International Conference on Physical Modelling in Geotechnics，2010:245 － 250，Zurich，Switzerland:Taylor＆ Francis Group，London.

［4］佟德纯，姚宝恒.工程信号处理与设备诊断(第一版)［M］.北京:科学出版社，2008.(TONG De-chun，YAO Bao-heng.Engineering Signal Processing and Equipment Diagnosing(First Edition)［M］.Beijing:Science Press，2008.(in Chinese))

［5］DIEF H M，FIGUEROA L.Shake Table Calibration and Specimen Preparation for Liquefaction Studies in the Centrifuge［J］.Geotechnical Testing Journal，2003，26(4):402－409.

［6］李京爽，侯瑜京，徐泽平，等.砂土自由场地基水平垂直振动离心模拟试验［J］.岩土力学，2011，32(增2):208 －214.(LI Jing-shuang，HOU Yu-jing，XU Ze-ping，et al.Centrifugal Modeling of Seismic Response of Freefield and Ground under Horizontal and Vertical Earthquakes［J］.Rock and Soil Mechanics，2011，32(Sup.2):208 －214.(in Chinese))