基于VAR模型的各类粮食国际价格波动关系分析

公茂刚，吴石磊，王学真

(1.山东理工大学 商学院，山东 淄博 255012;2.东北师范大学 商学院，吉林 长春 130117)

一、引 言

自进入21世纪以来，国际粮价波动幅度逐渐增大，特别是粮价上涨幅度越来越大。根据联合国粮农组织的数据，从2006年1月份到2008年4月份，世界谷物价格指数由107.9增加到274.1的最高点，增长了154%。由于粮价的大幅上涨，大量发展中国家因此遭受严重的粮食危机，人们的粮食安全受到威胁，不少国家还因此爆发动乱和流血冲突。2008年下半年以来，由于受到金融危机的影响，国际粮价开始逐步回落，到了2010年6月份，世界谷物价格指数降为151.2，与最高点相比，下降了约44.9%。自2010年7月份开始，国际粮价又开始了新一轮上涨，到2011年4月份，世界谷物价格指数265.4，接近于2008年的水平，此后国际粮价又开始回落。各类主要粮食作物的价格波动也体现出一定的相关关系，即一种粮食的价格波动将会对其他粮食的价格产生某种正面或负面的影响，这一点可以由图1明显的看出。粮价波动对粮食供给的稳定性及人们的粮食获取能力都会产生不利影响，进而会影响一国的粮食安全，因为粮食安全的两个核心要素就是粮食供给和粮食获取。因此，了解国际粮价的波动规律及各类粮食价格波动的相互关联有助于采取有效的措施稳定粮价，避免粮价波动的国际传导对国内粮食市场进而对粮食安全产生不利影响。

国际粮食价格波动问题一直备受学界关注，有较多学者从不同角度进行了研究。研究成果主要体现在以下三个方面.

1.国际粮价波动的模式。Bigman et al(1983)运用线性回归方法验证了芝加哥期货交易所小麦、玉米、大豆的期货价格与其现货价格间关系密切。Gilbert(2006)的研究表明农产品价格波动在20世纪60年代较低，但在70年代和80年代前半期较高，在20世纪80年代和90年代后半期回落，但仍远高于20世纪60年代的水平。Cooke＆Robles(2009)利用2002至2009年的月度数据分析了玉米、小麦、大米和大豆的国际价格变动情况。Gilbert＆Morgan(2010)利用GARCH(1，1)模型研究了2007～2009年的国际粮价波动模式，认为在这3年间粮食价格呈现较高波动性，花生油、大豆和豆油的条件异方差显著上升。

2.国际粮价波动的原因。粮价波动的重要来源被普遍认为是天气等自然因素对农业生产的冲击，然而需求冲击，尤其是收入冲击(Gilbert，2010)和政策冲击(Christiaensen，2009)也是粮价波动的主要原因。Lapp＆Smith(1992)认为，粮价波动水平直接和间接受到宏观经济政策特别是货币政策的影响。Pindyck(1994)认为短期内投机因素是解释粮价波动的重要变量。Schmidhuber(2006)，Tyner＆Taheripour(2008)均认为由于补贴及政府对生物产业的支持，使市场对玉米及大豆的需求倍增，造成粮价波动。Gilbert(2010)认为中国及其他亚洲经济体的快速增长是粮价高企的原因。Cooke＆Robles(2009)认为国际粮价波动主要是由期货市场上的金融投机行为导致。王文斌、戴金平(2009)认为国际粮价波动与粮食产量、粮食消费和粮食库存的变化存在密切关联。

3.国际粮价波动的影响。Caglayan＆Filiztekin(2003)的研究发现粮食产品价格的波动对通货膨胀率具有非线性影响。FAO(2009)认为国际粮价波动给低收入缺粮国家带来了粮食获取的风险，造成其粮食安全的脆弱性。Cranfield＆Haq(2010)利用QUAIDS(二次近似理想需求系统)分析了国际粮价波动对消费者福利的影响。孙国锋(2008)认为国际粮价的持续上涨会诱发全球通货膨胀、社会动荡乃至战争。丁守海(2009)认为国际粮价波动对我国粮价波动具有传递效应。金三林(2010)认为国际粮价波动对我国食品价格及CPI的影响越来越大，进口和期货市场是主要传导渠道。

对于国际粮价波动的研究虽已取得以上显著成果，但这些研究还主要以粮食总体为对象或者是分门别类的比较研究，很少将不同种类粮食的国际价格波动间关系作为研究对象。价格这类时间序列数据通常呈现出阶段性的较大波动和阶段性的相对稳定，即存在条件异方差，因此，目前有关粮食价格波动研究的主要方法也局限于ARCH类模型。但研究各类粮食国际价格的波动关系则需要采用VAR(向量自回归)模型。目前，VAR模型主要应用在汇率波动、货币政策冲击、以及能源价格波动等方面，在粮食价格波动关系的研究中应用的很少。鉴于此，本文将利用VAR模型、脉冲响应函数以及方差分解对稻米、小麦、玉米、大豆、高粱五类主要粮食国际价格波动间的关系进行实证研究。

二、模型设定与数据描述

VAR模型是由Sims(1980)提出的。VAR模型采用多方程联立形式，不以经济理论为基础，在模型的每一个方程中，内生变量对模型的全部内生变量的滞后项进行回归，从而估计全部内生变量的动态关系。一般的VAR(P)模型的数学表达式是:

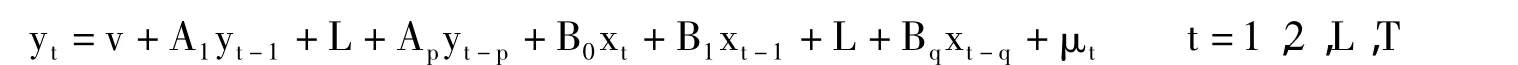
其中，yt=［y1tL ykt］′是 k维内生变量向量，xt=［x1tL xmt］′是m 维外生变量向量，A1到 Ap和 B1到 Bq分别时是k×k维和 k×m 维待估参数矩阵，假定 μt是白噪声序列，即 E(μt)=0，E(μtμt′)=∑，并且 E(μtμt′)=0(t≠s)。在本文中，所有的变量均为内生变量，即稻米、小麦、玉米、大豆和高粱的价格变量。

本文所采用的原始数据均来源于联合国粮农组织数据库(http://www.fao.org/economic/est/prices)，跨度从2000年1月到2011年12月，总共144个月份的数据。由于该数据库中关于各类粮食的价格有的并非一种，本文在选用的时候，为了能体现整个世界各类粮食价格的总体变化情况，本文对具有不同价格的某类粮食进行了简单的算数平均。比如稻米价格就是根据泰国A1级白碎米的曼谷FOB价和泰国100%B2级白米的曼谷FOB价两种交易价格进行简单算数平均计算得到的;小麦价格是根据阿根廷小麦上游FOB价、美国2号硬红冬小麦的墨西哥湾FOB价和美国2号软红冬小麦的墨西哥湾交货价三种交易价格简单算数平均计算得到;玉米价格是根据阿根廷玉米上游FOB价和美国2号黄玉米的墨西哥湾FOB价两种交易价格简单算数平均计算得到;高粱价格只有一种，采用的是美国2号黄高粱的墨西哥湾FOB价格;大豆价格也只有一种，采用的是美国1号黄大豆的墨西哥湾FOB价格。由于本文研究的是各类粮食国际价格的波动规律，因此，在采用VAR模型作波动分析前，需要首先对原始数据进行预处理。而由于价格的变动率更能反映价格的波动状况，因此，本文使用了同期价格变动率，即通过t年某月的价格与t－1年同一月份的价格计算出来的变动率来分析各类粮食国际价格的变动规律。稻米(rice)、小麦(wheat)、玉米(maize)、高粱(sorghum)、大豆(soybean)的价格变动率分别见图1。从图中可以明显看出各类粮食国际价格的变动率具有明显的同步性，即各类粮食国际价格都在同一时间段表现出相同的上升或下降趋势。各种粮食的国际价格变动率的描述性统计详见表1。各类粮食的价格变动率的峰值都大于正态分布的峰值3，表明价格变动率具有明显的尖峰厚尾的特征。由JB统计量可以看出，除高粱各类粮食的价格变动率都显著的异于正态分布，高粱的价格变动率在10%的显著性水平下也异于正态分布。

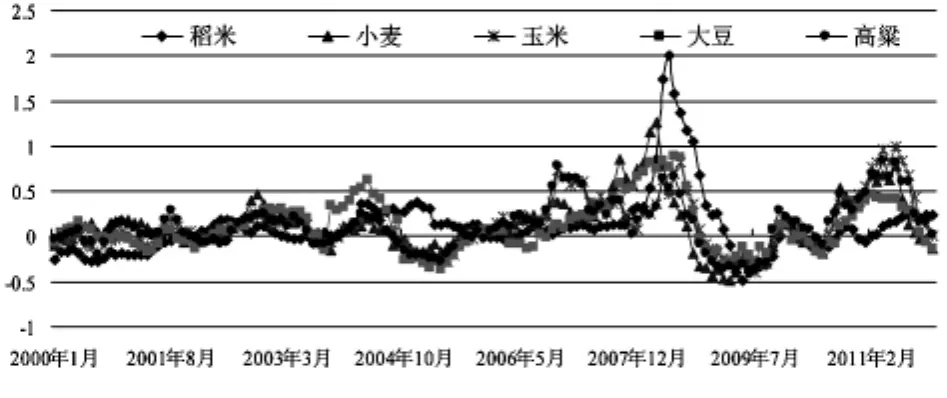
图1 2000年1月～2011年12月世界稻米、小麦、玉米、大豆、高粱价格变动率

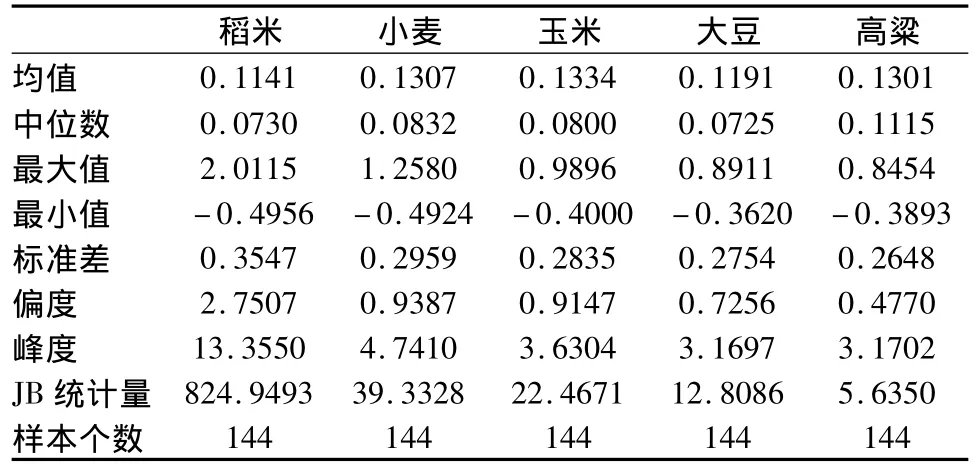
表1 各种粮食国际价格变动率的描述性统计

三、模型估计与结果分析

(一)建模前的相关检验

对于时间序列数据，为避免伪回归的产生，需要对其作平稳性检验。对各类粮食国际价格变动率的单位根检验如表2所示，从中可以看出，稻米、小麦、玉米和大豆的价格变动率在1%的显著性水平下是平稳的，高粱的价格变动率在5%的显著性水平下是平稳的。因此，各类粮食价格的变动率满足平稳性要求，可以进行进一步分析。接下来确定滞后阶数，根据SC准侧，选择滞后期数为1期，并建立一阶向量自回归。根据自回归特征多项式的检验结果，所有的根都在单位圆内，表明模型是稳定的，因此可以进行预测及下一步的分析。根据VAR的Granger因果关系Wald检验结果，小麦价格变动是稻米价格变动的格兰杰原因，且在1%的显著性水平下通过检验，玉米、大豆和高粱价格变动都不是稻米价格变动的格兰杰原因，但四者联合起来是稻米价格波动的格兰杰原因，且在1%的水平下显著;稻米、玉米、大豆价格变动都是小麦价格变动的格兰杰原因，且稻米在1%的水平下显著，玉米和大豆在5%的水平下显著，在10%的水平下高粱价格变动也是小麦价格变动的格兰杰原因，在1%的水平下，四者联合起来是小麦价格变动的格兰杰原因;小麦、高粱价格变动是玉米价格变动的格兰杰原因，且在1%的水平下显著，稻米、大豆价格变动不是玉米价格变动的格兰杰原因，但在1%的水平下，四者联合起来是玉米价格变动的格兰杰原因;小麦、玉米价格变动是大豆价格变动的格兰杰原因，且小麦在1%的水平下显著，玉米在5%的水平下显著，稻米和高粱价格变动不是大豆价格变动的格兰杰原因，但在1%的水平下，四者联合起来是大豆价格变动的格兰杰原因;小麦价格变动是高粱价格变动的格兰杰原因，且在1%的水平下显著，稻米、玉米和大豆价格变动都不是高粱价格变动的格兰杰原因，但在在1%的水平下，四者联合起来是高粱价格变动的格兰杰原因。

(二)脉冲响应分析

VAR模型的主要功能并不是分析一个变量的变化如何影响另一个变量，而是分析当一个误差项发生变化，或者说模型受到某种外部冲击时对系统的动态影响，这就需要脉冲响应函数对其进行分析。图2显示了各变量的累积脉冲响应函数结果。图2的上左图是稻米价格变动率对模型中各变量的单位Cholesky标准差新息正向冲击的脉冲响应累积图。从中可以看出，稻米价格变动率对其自身冲击的响应起初为正，即方向一致，且在前6期逐渐增长，从第7期开始下降，到第17期降为负值，即方向相反，且该负向作用具有持久效应。稻米价格变动率对小麦冲击的响应为正，且在前18期逐渐增长，此后有所下降，但最终在0.7左右达到稳定。稻米价格变动率对玉米冲击的响应为负，从图中可以看出，虽然该负向响应有所波动，但最终趋于平稳，维持在－0.27左右。大豆冲击对稻米价格波动的影响第1期为0，第二期为负，但此后一直为正，且在第24期达到最大值，之后有所下降，但最终在0.56左右达到稳定。高粱冲击对稻米价格波动的影响在第1期为0，第二期开始为负，直到第14期变为正，并一直持续下去，但从图中可以看出，高粱冲击对稻米价格波动的效应很小，几乎为0。

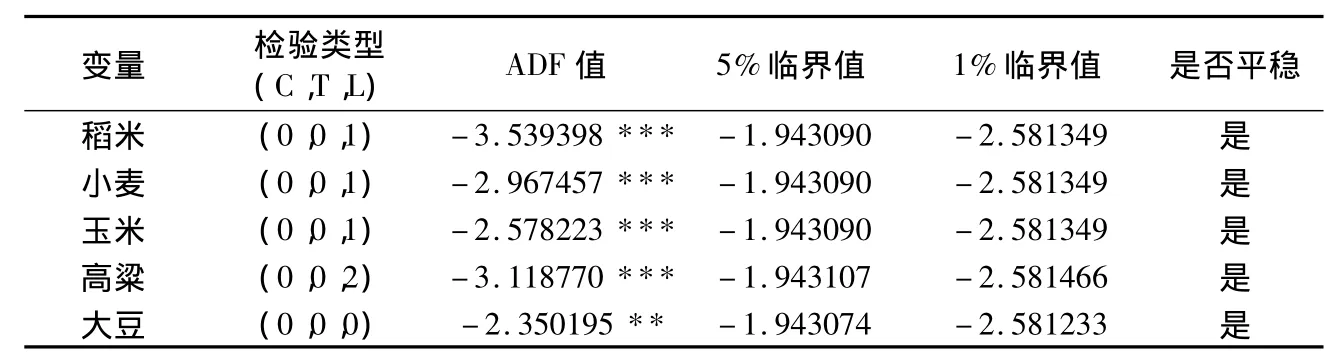
表2 各类粮食国际价格变动率的单位根检验

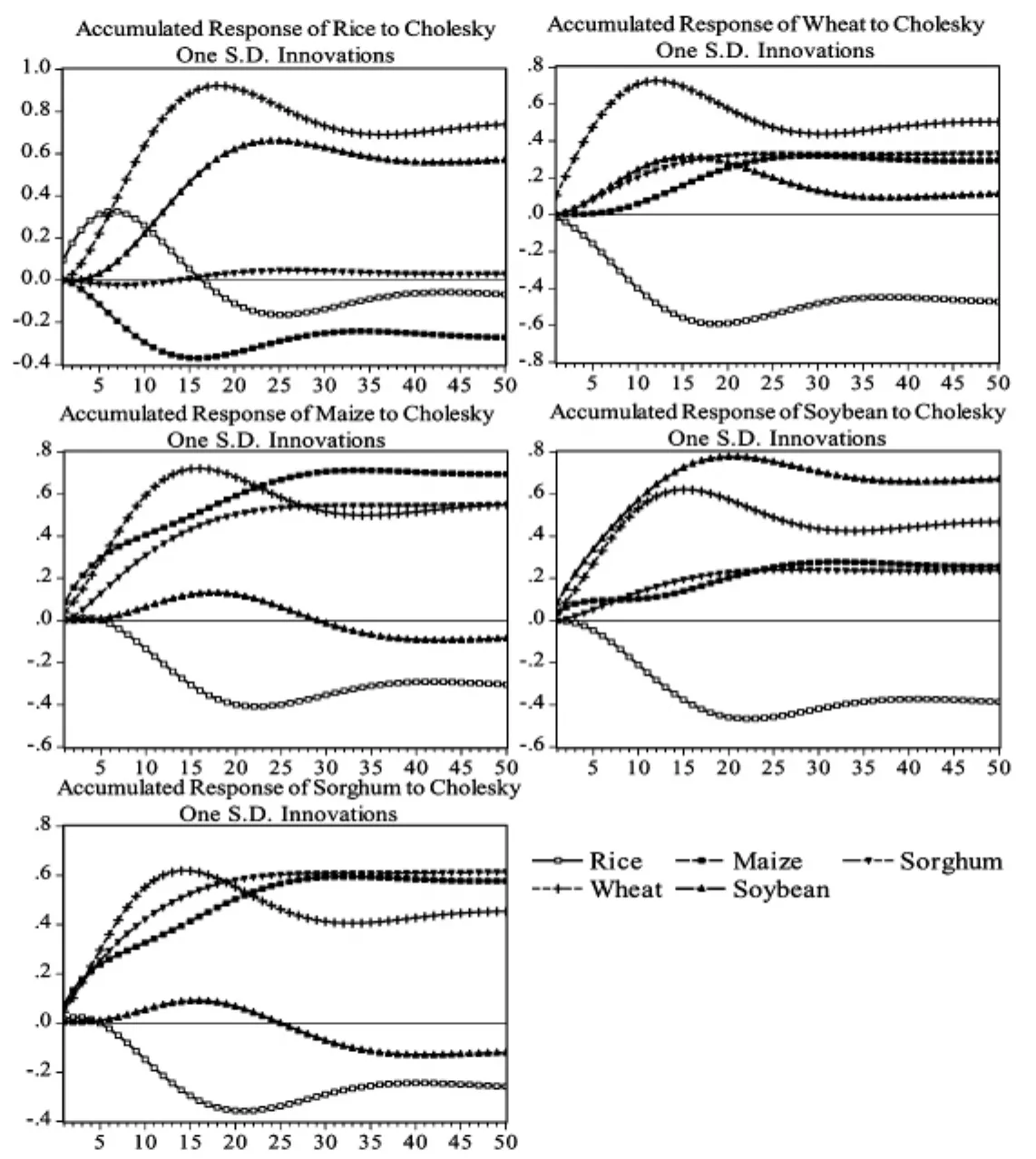
图2 各变量的累积脉冲响应函数图

图2的上右图是小麦价格变动率对模型中各变量的单位Cholesky标准差新息正向冲击的脉冲响应累积图。该图显示，小麦价格变动率对其自身冲击的响应为正，且前12期逐渐增长，此后开始下降，最终在0.5左右达到稳定。小麦价格变动率对稻米冲击的响应为负，在19期，负向影响达到最大值－0.59，此后有所上升，但最终在－0.46左右趋于稳定。小麦价格变动率对玉米冲击的响应为正，其逐渐增长，但最终趋于平稳，维持在0.3左右。大豆冲击对小麦价格波动的影响一直为正，虽然有所波动，但最终在0.1左右趋于平稳。高粱冲击对小麦价格波动的影响也一直为正，并持续增长，并最终在0.33左右趋于平稳。

图2的中左图是玉米价格变动率对模型中各变量的单位Cholesky标准差新息正向冲击的脉冲响应累积图。该图显示，玉米价格变动率对其自身冲击的响应为正，且持续增长，最终在0.7左右趋于稳定。玉米价格变动率对稻米冲击的响应前5期为正，此后为负，虽然有所波动，但最终在－0.3左右趋于稳定。玉米价格变动率对小麦冲击的响应为正，前16期逐渐增长，此后开始下降，但最终趋于平稳，维持在0.54左右。大豆冲击对玉米价格波动的影响前29期为正，且先增后降，此后为负，最终在－0.08左右趋于平稳。高粱冲击对玉米价格波动的影响一直为正，并持续增长，并最终在0.54左右趋于平稳。

图2的中右图是大豆价格变动率对模型中各变量的单位Cholesky标准差新息正向冲击的脉冲响应累积图。该图显示，大豆价格变动率对其自身冲击的响应持续为正，且逐渐增长，第20期达到最高，此后有所下降，但最终在0.66左右趋于平稳。大豆价格变动率对稻米冲击的响应为负，且该负向效应逐渐增长，并在－0.38左右趋于稳定。大豆价格变动率对小麦冲击的响应为正，虽然该正向响应先增后减，但最终趋于平稳，维持在0.46左右。玉米冲击对大豆价格波动的影响为正，且持续增长，但最终在0.25左右达到稳定。高粱冲击对大豆价格波动的影响也持续为正，并逐渐增长，最重趋于稳定，维持在0.23左右。

图2的下左图是高粱价格变动率对模型中各变量的单位Cholesky标准差新息正向冲击的脉冲响应累积图。该图显示，高粱价格变动率对其自身冲击的响应持续为正，且逐渐增长，并最终在0.61左右趋于平稳。高粱价格变动率对稻米冲击的响应前4期为正，此后为负，且该负向效应逐渐增长，并在－0.25左右趋于稳定。高粱价格变动率对小麦冲击的响应为正，虽然该正向响应先增后减，但最终在0.45左右趋于平稳。玉米冲击对高粱价格波动的影响为正，且持续增长，并在0.57左右达到稳定。大豆冲击对高粱价格波动的影响前24期为正，且先增后降，此后为负，并最终在－0.11左右趋于稳定。

(三)方差分解

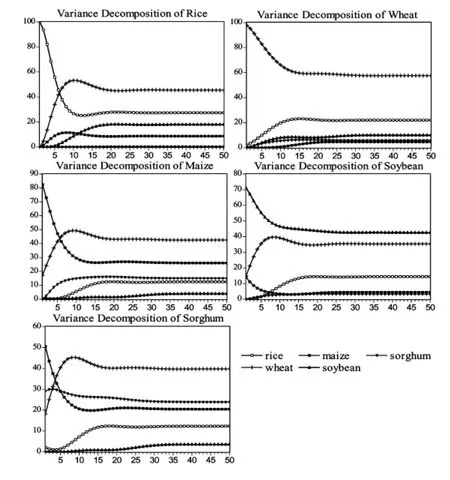
图3 各变量的方差分解图

脉冲响应函数主要用来度量系统的干扰对某一变量的影响效果，而方差分解则可以分析VAR模型中每一个外部冲击对内生变量变化的贡献度，它是从另一种角度来描述系统动态性的方法。图3显示了各变量的方差分解图。图3的上左图是稻米价格变动率方差分解图，从中可见，除其自身的贡献度逐渐降低外，其他各变量冲击的贡献度都逐渐增加，所有贡献度都最终趋于平稳，贡献度由大到小依次为小麦、稻米、大豆、玉米、高粱，其中高粱的贡献度几乎为0。图3的上右图是小麦价格变动率方差分解图，其自身的贡献度逐渐降低，其他各变量冲击的贡献度都逐渐增加，但都最终趋于平稳，贡献度由大到小依次为小麦、稻米、大豆、高粱、玉米，其中高粱和玉米的贡献很接近。图3的中左图是玉米价格变动率方差分解图，其自身的贡献度逐渐降低，其他各变量冲击的贡献度都逐渐增加，但都最终趋于平稳，贡献度由大到小依次为小麦、玉米、高粱、稻米、大豆。图3的中右图是大豆价格变动率方差分解图，其自身及玉米的贡献度逐渐降低，其他各变量冲击的贡献度都逐渐增加，但都最终趋于平稳，贡献度由大到小依次为大豆、小麦、稻米、玉米、高粱，其中玉米和高粱的贡献度十分接近。图3的下左图是高粱价格变动率方差分解图，其自身及玉米的贡献度逐渐降低，其他各变量冲击的贡献度都逐渐增加，都最终趋于平稳，贡献度由大到小依次为小麦、高粱、玉米、稻米、大豆。

四、结 论

通过上述分析，本文得出以下两点结论。

1.各类粮食国际价格波动存在明显相关性。来自稻米和玉米的外部冲击对稻米价格波动具有持久的负向效应，来自小麦和大豆的外部冲击对稻米价格波动具有持久正向效应，高粱冲击对稻米价格波动影响很小。稻米冲击对小麦价格波动具有持久的负向效应，小麦、高粱、玉米、大豆冲击对小麦价格波动具有持久正向效应。来自稻米和大豆的外部冲击对玉米价格波动具有持久负向效应，玉米、高粱、小麦冲击对玉米价格波动具有持久正向效应。稻米冲击对大豆价格波动具有持久负向效应，来自大豆、小麦、玉米、高粱的外部冲击对大豆价格波动具有持久正向效应。来自稻米和大豆的外部冲击对高粱价格波动具有持久负向效应，高粱、玉米和小麦冲击对高粱价格波动具有持久正向效应。

2.各类粮食价格变动率外部冲击对内生变量波动的贡献度不同。稻米冲击对其自身及小麦价格波动的贡献度较大，对其他粮食价格波动贡献度也较为明显;小麦冲击对稻米、小麦、玉米和高粱价格波动的贡献度最大;玉米冲击对其自身及高粱价格波动贡献度较大，对其他贡献度较小;大豆冲击对其自身价格波动的贡献度最大，但对其他粮食价格波动的贡献度不大;高粱冲击对其自身价格波动贡献度较大，但对其他粮食价格波动贡献不大，其中对稻米价格波动贡献度最小。