月球软着陆动力学分析与仿真

罗松柏 赵永嘉

（北京航空航天大学 自动化科学与电气工程学院，北京 100191）

月球软着陆动力学分析与仿真

罗松柏 赵永嘉

（北京航空航天大学 自动化科学与电气工程学院，北京 100191）

以4腿式月球探测器为研究对象，分析了探测器的部件结构与物理属性、月球物理环境等综合因素.在探测器动力学研究中，提出了一种基于结构的分块参数化仿真方法，分析探测器着陆时的受力，建立着陆腿与足垫等关键部件的动力学模型，利用简化探测器结构，综合各部分模型.结合虚拟现实可视化仿真技术，实现月球软着陆过程仿真.通过仿真反映出月面坡度与着陆速度、刚度系数与阻尼系数等初始条件对软着陆效果的影响，验证方法的有效性.该方法已成功应用于登月工程研究.

月球软着陆;动力学;结构;仿真

月球软着陆技术是我国探月工程的一项关键技术.为了保障探测器上搭载的设备与人员的安全，使得探测器平缓、顺利地着陆在月球表面，防止出现着陆器过载与倾倒，必须对月球软着陆过程进行严格的动力学分析与研究.目前，国内外学者在月球软着陆技术方面进行了大量的研究［1－3］.研究工作主要集中在对探测器上的缓冲装置进行整体的动力学分析，例如文献［4－5］对铝蜂窝结构进行了动力学分析，文献［3］提出了一种感应磁阻尼的新型缓冲结构，文献［6］分析了液压/气压软着陆缓冲装置.但是月球软着陆是一个复杂的过程，不仅仅依赖于缓冲装置，还受诸多因素影响，而且整体上分析得到的动力学模型复杂且不通用，不具有可扩展性和仿真实时性.

针对上述问题，本文提出了一种基于结构的分块参数化仿真方法，对月球软着陆进行仿真，提高了仿真的真实感与实时性.

1 月球软着陆综合因素分析

月球软着陆在探测器本身动力学性能以外还受多种综合因素影响.针对动力学仿真的实际需要，重点讨论了其中最为重要的两项因素:探测器的结构与月表环境.

1.1 探测器结构分析

通常的月球探测器动力学研究缺少对结构因素的单独分析，只是直接对探测器整个缓冲装置进行动力学建模仿真，有如下不足:①通用性差，只能针对特定的探测器，当探测器结构、材料改变时不可扩展;②模型复杂，仿真实现困难，且不满足仿真实时性要求.

针对上述问题，本文对动力学分析仿真方法进行了改进.首先分析探测器结构并做简化，然后进一步分析探测器软着陆时的受力情况，对其中的关键部件建立合理的参数化模型.提出了一种基于结构的分块参数化仿真方法.探测器的改变只需要对模型结构和物理参数进行相应的修改，通用性增强.从各个部件的角度建立动力学模型并考虑整体结构，更加符合实际情况，模型更加简化且真实性增强.

采用4腿式月球探测器进行结构分析与建模仿真.其外形如图1a，由探测器主体和软着陆机构两部分组成.探测器主体搭载有效载荷，软着陆机构连接在主体上发挥缓冲与支撑作用［7］，是实现探测器软着陆的关键，由安装有缓冲器的主着陆腿、刚性辅助支撑腿、塑性足垫和展开锁定机构组成.各部分基本功能如表1所示.

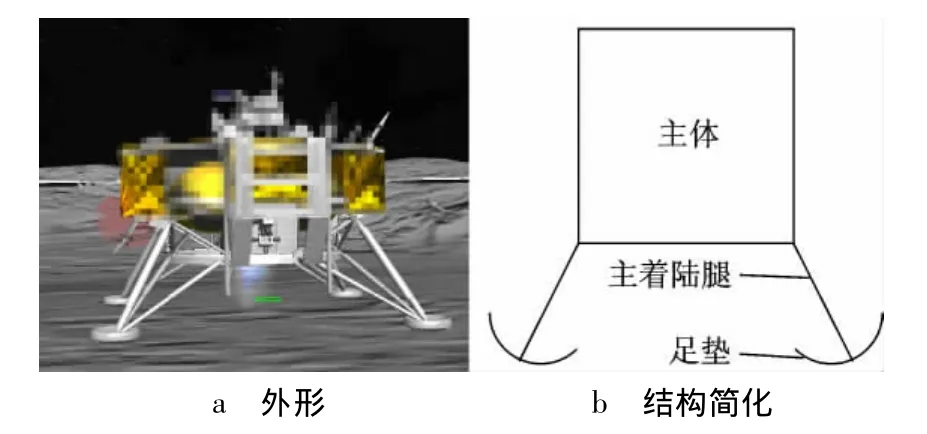
图1 探测器模型及其结构简化示意图

表1 软着陆机构基本组成与功能

由表1可以看出，缓冲器在着陆瞬间吸收主要的纵向冲击能量;足垫吸收部分纵向冲击能量，并吸收主要的横侧向冲击能量，防止探测器发生侧滑.这两部分是探测器软着陆的关键部件.对于动力学分析，重要的是探测器整体着陆性能，探测器主体的内部结构，与软着陆无关的设备对探测器着陆性能影响很小，因此可将探测器模型结构进行简化，图1b为简化示意图.

1.2 月表环境分析

月表环境包括近月环境与月面环境，是影响月球软着陆效果的重要因素之一.考虑到物理建模与仿真实际要求，需要着重注意以下几点:

1）近月重力加速度为g月=1.63 m/s2;

2）月表真空度为 2.7×10－10Pa，属于高度真空;

3）月壤平均厚度为5～10 m，平均密度为1500 ～2500 kg/m3，结合力为 0.02 ～0.20 N/m2，有效摩擦因数约为 0.4 ～0.8［7］;

4）月表主要由高地、月海和环形坑组成，地形斜度最大约39°，撞击坑外侧一般都小于25°，月表高地小于30°，月海地区相对平坦，最大坡度为 17°.

2 探测器关键部件动力学建模

在简化探测器结构的基础上，通过对探测器软着陆时的受力情况进行分析，分别建立各关键部件的统一动力学模型，以实现简单、真实、仿真实时性与扩展性好等目标.

2.1 缓冲器的动力学模型

探测器着陆机构通常采用对称结构，各着陆腿的动力学性能一致，只需取其中一条进行分析.目前，多腿式月球探测器软着陆机构上主要采用的缓冲器有铝蜂窝缓冲器和液压缓冲器.

1）铝蜂窝缓冲器动力学分析.铝蜂窝缓冲器通过压缩内筒中的铝蜂窝材料，如图2所示，产生变形来吸收冲击能量，具有质量轻、缓冲行程长和工作可靠等优点.

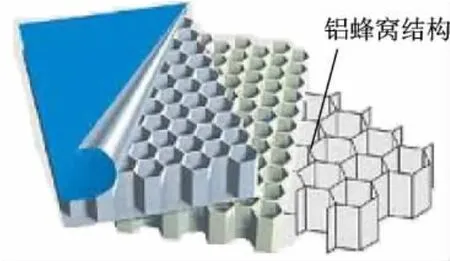
图2 铝蜂窝材料

当铝蜂窝材料被压缩时，应力应变曲线可分为:弹性段、屈服段及致密段.弹性段与屈服段比为小量，可先忽略其弹性，通过永久变形吸收能量实现缓冲，压缩时做的总功为

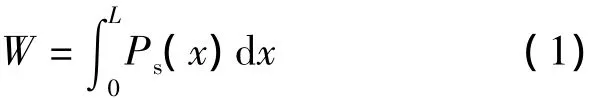
式中，Ps（x）为铝蜂窝静态压缩载荷;L为总缓冲行程;x为压缩变形量.如将压缩过程中垮塌载荷看作恒力，则平均载荷为

此Ps作为静垮塌载荷，对同一类型蜂窝来说是一个定值，可通过大量试验得到.在实际情况中，铝蜂窝在不同冲击速度下，其垮塌载荷也不同，用垮塌系数η表示动垮塌载荷Pd与Ps的关系如下［5］:

η可以采用二次多项式近似表达:

式中，a，b为待定系数，不同型号的铝蜂窝具有不同数值，可由实验测得;val为铝蜂窝的冲击速度.

假设mal为铝蜂窝缓冲器所支撑的等效探测器质量，xal为铝蜂窝实际缓冲行程，由式（3）、式（4）可以推出铝蜂窝缓冲器的运动微分方程为

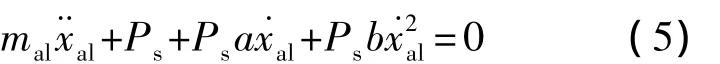
如果考虑铝蜂窝的弹性，并假设铝蜂窝的刚度系数为Kal，式（5）进一步演变为

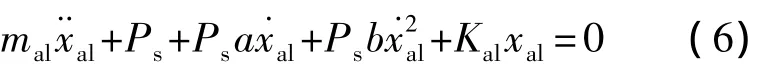
2）液压缓冲器动力学分析.液压缓冲器的结构如图3所示，液体密封在缓冲器的缸体内部，缓冲器吸能时向两侧流动.探测器在月球表面着陆时，着陆腿受外力作用推动活塞运动，液体流经阻尼孔，产生缓冲阻尼力.同时，由于弹簧和被压缩的液体反弹，推动活塞反向运动，缓冲器最后能够恢复姿态.液压缓冲器具有缓冲平缓，吸能后能恢复等优点.

图3 液压缓冲器结构

假设内外腔液压作用面积相等，都为A，忽略杆与内壁的摩擦力，液压缓冲器的运动微分方程为

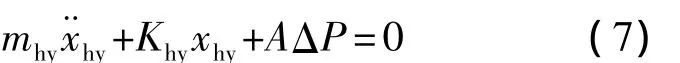
式中，mhy为液压缓冲器所支撑的等效探测器质量;xhy为液压缓冲器缓冲行程;Khy为弹簧刚度系数;ΔP为内外腔的压力差.ΔP与液压缓冲器活塞速度vhy之间有对应函数关系，如图4所示［8］.

①以流域及河流水量分配方案以及治理规划来细化明确用水总量控制和重要断面水量控制指标，地表水主要包括石羊河的蔡旗断面、黑河的莺落峡和正义峡断面、疏勒河的双墩子和西湖断面；地下水主要包括武威盆地、民勤盆地、张临高盆地、酒泉盆地的水位水量控制指标，生态敏感点水位水量控制包括民勤青土湖、敦煌西湖湿地管理控制指标。

图4曲线可近似看作分段线性曲线，液压缓冲器的阻尼系数为ACi，其中，Ci为各分段直线的斜率，式（7）转化为

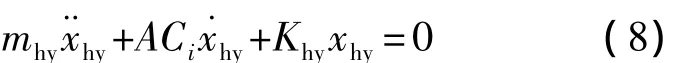
3）着陆腿动力学模型.由式（6）、式（8）可以看出，铝蜂窝缓冲器和液压缓冲器的运动微分方程都可以等效为有阻尼自由振动微分方程，其中阻尼系数和刚度系数可能是一个非线性变化的量，可以通过分段线性来进行模拟.着陆腿缓冲器动力学等效模型如图5所示.

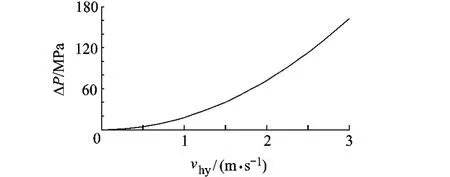
图4 液压缓冲器的ΔP－vhy关系曲线

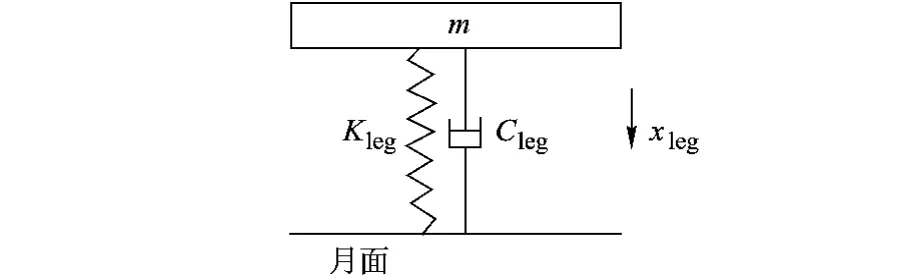
图5 缓冲器简化模型

取平衡位置为坐标原点，振动方程中不考虑重力影响.着陆腿缓冲器的运动微分方程为有阻尼自由振动微分方程的标准形式:

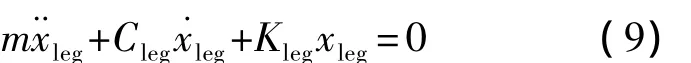
式（9）是着陆腿缓冲器的统一参数化模型，Kleg与Cleg反映了着陆腿缓冲器的物理属性.

2.2 足垫的动力学模型

足垫是探测器与月面直接接触的部件，在着陆腿末端用球铰链与着陆腿相连，有一定的缓冲能力.足垫与月壤的接触作用力包括法向接触力和切向摩擦力两部分.法向接触力可以等效为弹簧阻尼模型，接触力方程为

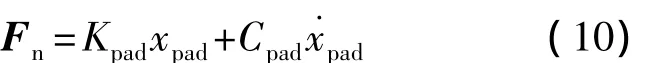
式中，Kpad，Cpad为与接触变形xpad和变形率相关的足垫的刚度和阻尼系数.

切向摩擦力可以等效为库仑摩擦模型，假设μ为足垫与月面的摩擦系数，则接触力方程为

式（10）、式（11）是足垫的统一参数化模型，Kpad和Cpad以及μ反映了足垫的物理属性.

3 月球软着陆仿真实现

3.1 月球环境参数设置

由前文月表环境分析，将月球物理环境的重力加速度参数设置为1.63 m/s2.同时，由于月表环境为高度真空，忽略探测器着陆时空气阻力.

月壤对于着陆效果有重要影响，它的密度决定了着陆时足垫下陷深度、缓冲力大小以及缓冲时间长短;月壤与足垫的横向相互作用摩擦系数决定了探测器能以多大的水平速度着陆而不倾覆.根据前文分析，将密度设置为2 000 kg/m3;摩擦系数设置为μ=0.45（近似认为静摩擦系数与动摩擦系数一致）.

月面地形特点也是影响着陆效果的关键性因素.为了模拟月球上不同着陆地点的地形特点，本文将仿真中地形的坡度设为可调的，能够全面的模拟高地、月海和环形坑.

3.2 探测器整体模型实现

在3dsmax中构造探测器模型（图6），将模型整体拆分为探测器主体、4条着陆腿与4只足垫，共9部分，分别对各部分建立物理实体模型，如图6中被框包围的是经过简化的探测器各部分物理实体.

图6 探测器模型与简化

依据某探测器实际情况，各部件基本参数设置如下:主体质量为1 200 kg，主体尺寸为2 m×1.5 m×2 m;着陆腿质量为 100 kg，着陆腿尺寸为0.30 m× 1.55 m× 0.30 m;足垫质量为 15 kg，足垫尺寸为0.46 m×0.16 m×0.46 m.

3.3 着陆腿与足垫模型实现

足垫是着陆时首先触月的部件，与主着陆腿以球铰链方式连接，具有2个方向上的转动自由度.当其受到月表作用力时，会通过铰接关节传给主着陆腿一个沿着陆腿轴向上的力.着陆腿分为着陆腿上部与下部，通过滑动关节连接，具有轴向的滑动自由度，作用力经过缓冲器模型最后传至主体.根据上述分析，建立着陆腿与足垫的模型如图7所示.

着陆腿（缓冲器）缓冲过程简化模型为式（9），该模型由连接着陆腿上部与下部的滑动关节模拟.图7a为着陆腿滑动关节结构.滑动轴向设置为探测器主体中心与着陆腿中心的连线.

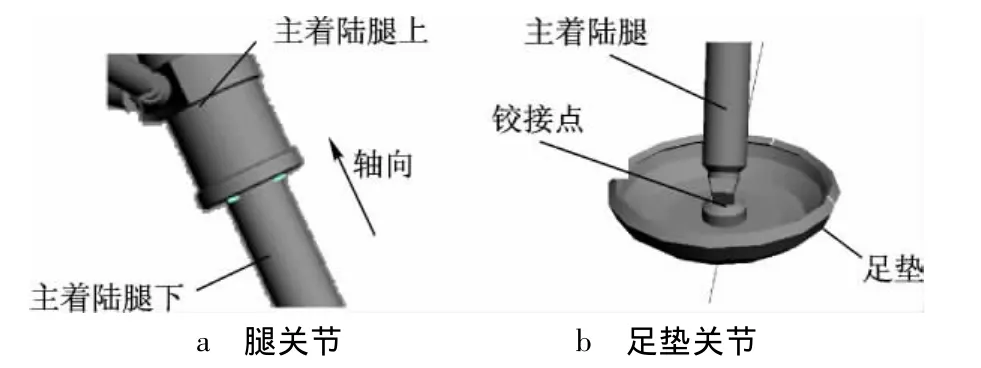
图7 着陆腿与足垫结构示意图

足垫的动力学模型为式（10）、式（11），该模型由足垫与着陆腿之间的球铰链关节模拟.图7b为足垫关节结构.铰接点设置在着陆腿的末端.

关节的参数主要有错误消减参数PERP与柔约束和约束力混合PCFM，其设置依据［9］为

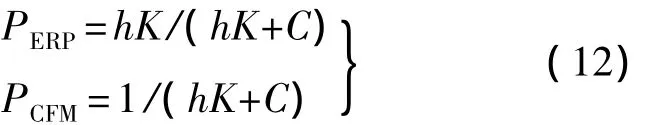
式中，K和C可以是着陆腿的Kleg和Cleg，也可以是足垫的Kpad和Cpad.通过式（12），缓冲器与足垫的动力学参数化模型转化为仿真中参数化模型.

对于足垫模型，其μ已在月球环境参数设置中设定为 0.45.

3.4 仿真流程

仿真流程图如图8所示.

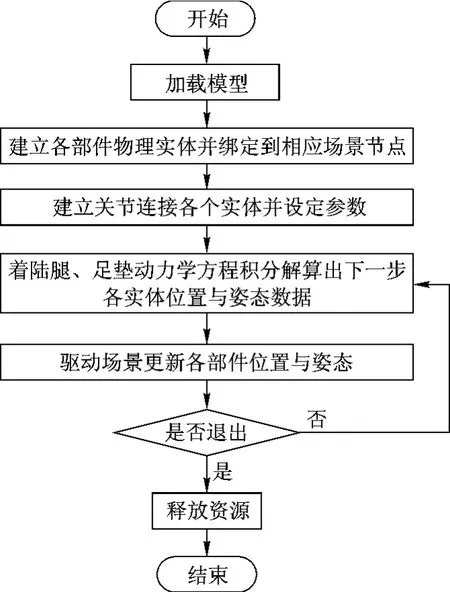
图8 仿真流程图

4 仿真结果分析

本文设计2组实验:①不同月面坡度θ下的最大着陆速度;②缓冲器刚度系数与阻尼系数改变对着陆效果的影响，以此验证本文方法.

1）θ与着陆速度v对着陆效果的影响.设置着陆腿Kleg=50kN/m，Cleg=6kN·s/m;足垫Kpad=40 kN/m，Cpad=2 kN·s/m.假设探测器以水平姿态着陆，在仿真平台中测出各种θ下允许着陆的最大高度hmax，然后根据能量守恒原理，求出允许着陆的最大速度vmax.

测试结果如表2所示.

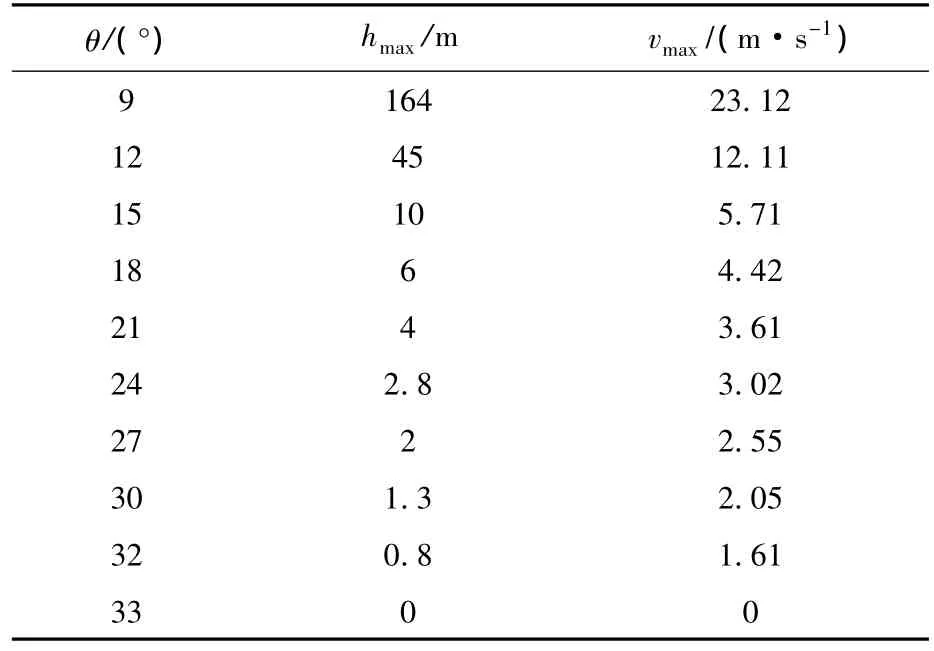
表2 θ 与 hmax，vmax关系

θ与v关系如图9a所示，斜线部分为允许着陆区域.可以看出，随着θ的增加，允许着陆速度的最大值vmax越来越小，当θ增加到某一临界值，探测器便不能稳定的静立在月面上，vmax降至0.

例如，θ=15°，当 v=4.42 m/s时，探测器状态位于图中的允许着陆区域，其着陆时的状态截图如图9b所示，图中的探测器稳定的着陆在月面之上.当v=6.25 m/s时，探测器状态不在图中的允许着陆区域，图9c为此时的软着陆状态截图，图中的探测器由于过大的冲击力而弹起倾覆.

2）刚度系数与阻尼系数对着陆效果的影响.选用不同材质和型号的缓冲器，其刚度系数和阻尼系数各不相同，会对探测器的着陆效果产生影响.当缓冲器的刚度系数过小时，着陆腿的支撑能力变弱可能导致探测器主体直接触地，刚度系数过大时，探测器软着陆过程的缓冲行程变小，缓冲效果向“硬着陆”靠近.当缓冲器阻尼系数过小时，探测器震荡加剧，稳态时间变长;当阻尼系数过大时，缓冲时间变短，着陆器缓冲效果变差.

例如，v=4.42 m/s，θ=5°时，如果着陆腿Kleg=50 kN/m，Cleg=6 kN·s/m，探测器软着陆时的位置变化曲线如图10a中的实线所示，探测器着陆后反弹较小，能够迅速稳定;如果着陆腿Kleg=50 kN/m，Cleg=0.6 kN·s/m，探测器软着陆时的位置变化曲线如图10a中的虚线所示，探测器着陆后反弹过大，振荡加剧，稳定时间较长.过大的反弹和稳定时间会对设备产生不利影响，且有可能造成探测器倾覆.

图10b和图10c是以上两种情况探测器着陆后第1次弹起至最大高度时的截图.由图可以看出，第1种情况反弹小，探测器姿态稳定;第2种情况反弹大，探测器姿态变化大，容易失去平衡.

图9 仿真测试结果1

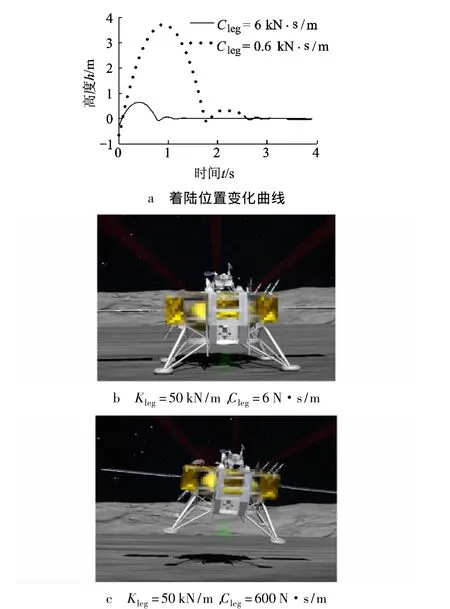
图10 仿真测试结果2

5 结论

仿真结果表明:本文方法能够直观、真实地反应出着陆情况，对月面坡度与着陆速度、刚度系数与阻尼系数等初始条件对着陆效果的影响能够准确地做出响应，具有良好的真实感与实时性.同时参数化的设计使得仿真的扩展性增强.仿真结果验证了本文方法的有效性.

（References）

［1］Hilderman R A，Mantus M，Lerner E.Landing dynamics of the lunar excursion module（method of analysis）［R］.AIAA-66A-42771，1966

［2］王少纯，邓宗全，高海波，等.微小型月球着陆器冲击隔离着陆腿研究［J］.哈尔滨工业大学学报，2004，36（2）:180－182

Wang Shaochun，Deng Zongquan，Gao Haibo，et al.Design of impact isolating landing legs for micro-miniature lunar lander［J］.Journal of Harbin Institute of Technology，2004，36（2）:180－182（in Chinese）

［3］Thompson W C.Dynamic model investigation of the rough-water landing characteristics of a spacecraft［R］.AIAA Paper-67-23281，1967

［4］蒋万松，黄伟，王海涛.ADAMS用户子程序在软着陆动力学仿真中的应用［J］.航天返回与遥感，2009，30（4）:11－18

Jiang Wansong，Huang Wei，Wang Haitao.Application of DAMS user-written subroutine to simulation of soft-landing dynamics［J］.Spacecraft Recovery and Remote Sensing，2009，30（4）:11－18（in Chinese）

［5］Jooahn L，John C.Lunar lander conceptual design［M］.US:NASA，1989

［6］陈金宝，聂宏，赵金才.月球探测器软着陆缓冲机构关键技术研究进展［J］.宇航学报，2008，29（3）:731－735

Chen Jinbao，Nie Hong，Zhao Jincai.Review of the development of soft-landing buffer for lunar explorations［J］.Journal of Astronautics，2008，29（3）:731－735（in Chinese）

［7］胡亚冰，孙毅.月球探测器软着陆机构［J］.上海航天，2010（1）:43－50

Hu Yabing，Sun yi.Soft lander of lunar lander［J］.Aerospace Shanghai，2010（1）:43－50（in Chinese）

［8］张文斌，周晓军.液压缓冲器特性计算与仿真分析［J］.农业机械学报，2008，39（7）:164－168

Zhang Wenbin，Zhou Xiaojun.Simulation and characteristic analysis of hydraulic bumper［J］.Transactions of the Chinese Society of Agricultural Machinery，2008，39（7）:164－168（in Chinese）［9］Russell Smith.Open dynamics engine［EB/OL］.http://www.ode.org/ode-docs.html

Dynamic analysis and simulation of soft-landing for lunar lander

Luo Songbai Zhao Yongjia
（School of Automation Science and Electrical Engineering，Beijing University of Aeronautics and Astronautics，Beijing 100191，China）

Taking the four-leg lunar lander as the study object，the lander’s component structure and lunar physical attribute was analyzed.When studying the lander’s dynamics，a block parameter simulation method based on structure was proposed，which analyzes the lander’s dynamic behavior during the landing moment，derives the buffers’and foot pads’dynamic model individually and integrates each model through simplifying lander’s structure.Technology of visual simulation was introduced and simulation of lunar-landing was realized.The effects of different initial conditions，such as slop of lunar surface and lading velocity，stiffness coefficient and damping coefficient were measured through simulation.The result verifies the validity of the method.This method has already successfully applied in engineering research of lunar-landing.

lunar landing;dynamics;structure;simulation

TP 391.9

A

1001-5965（2012）02-0185-06

2010-11-10;< class="emphasis_bold">网络出版时间:

时间:2012-02-21 11:47;

CNKI:11-2625/V.20120221.1147.028

www.cnki.net/kcms/detail/11.2625.V.20120221.1147.028.html

国家高技术研究发展计划资助项目（2009AA01Z333）

罗松柏（1986－），男，四川成都人，硕士生，ericluo95@gmail.com.

（编 辑:刘登敏）