基于D－P准则的深埋隧道破碎化分区规律研究

鲁 稳，古少枫，侯宜润

(华南理工大学土木与交通学院岩土工程系，广州 510641)

0 引言

21世纪是地下空间开发的世纪，地下空间开发以其节能安全而将取得长足的发展。大型地下电站、隧道、地铁等将随着国民经济的发展而大规模兴建。综观当今世界，有识之士已把对地下空间开发利用作为解决城市资源与环境危机的重要措施，是解决我国可持续性发展的重要途径［1］。

地下洞室开挖前，岩体在自重和构造(初始应力场)作用下处于相对稳定和平衡状态。洞室开挖后，由于开挖面处解除了约束，破坏原始平衡状态，致使地层发生应力重分布，达到新的平衡状态，称为二次应力状态［2］。此时，洞壁径向应力为零，切向应力剧增，洞周进入塑性平衡状态。围岩塑性破坏由洞周开始逐渐向深部岩体发展，直至稳定，洞周围岩形成一个松动区域，称之为松动区，或叫破碎区。松动岩体宏观主要表现为微裂隙增多，变形突然增大，内聚力、内摩擦角和变形模量降低［3］。

近年来，深部围岩轴对称破碎化分区的弹塑性解答有了长足的发展［4］，对围岩松动区进行三维有限元分析比较广泛［5－6］，而埋深对松动区半径影响的研究则相对较少。本文结合某深埋隧道工程，通过三维弹塑性有限元数值模拟，分析围岩松动区范围随隧道埋深的变化情况，以期对隧道围岩稳定性分析、确定合理的支护措施以及制定合理的开挖方案具有指导意义。

1 研究方法

圆形洞室在双向等压状态下，塑性区半径的弹塑性解答，可由以Mohr-Coulomb强度准则为极限平衡条件的修正的芬纳公式(Fenner，1938年)或卡斯特纳(H.Kastner)公式计算。

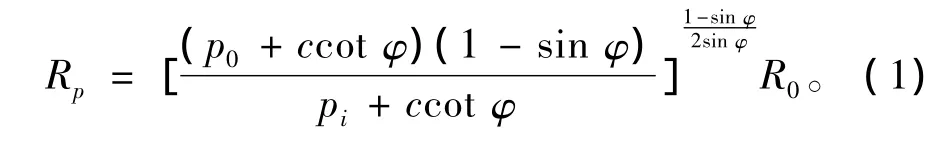
式中:p0为地应力;c，φ为围岩黏聚力和摩擦角;R0为隧道开挖半径;pi为衬砌与围岩相互作用力。

图1为岩石典型的应力－应变曲线。岩石由加载到破坏经历3个阶段:弹性阶段、塑性屈服阶段和破坏(破碎)阶段，相应隧道围岩随距轴心距离r不同而处于松动区、塑性区、弹性区3种状态(见图2)。通常取峰值点作为岩石的抗压强度σb，实际情况下很难判定岩石的屈服，其屈服强度与抗压强度存在一定的关系，二者比值即为屈强比。根据文献［7］的结果，在掌子面接近和通过选择断面时(±0.5B)，Ⅰ区围岩应力状态将经历急剧变化:拱顶和边墙处最大主应力和中间主应力快速增加后又迅速减小，而最小主应力则逐渐减小到一个很小的值后稳定，即为掌子面效应。其应力莫尔圆变化如图3所示，洞周围岩迅速屈服并破坏，由于应力重分布使Ⅱ区围岩塑性屈服，但尚未达到破坏条件，Ⅲ区围岩则处于弹性变形阶段。

自1900年Mohr-Coulomb强度理论提出以来，由于它能较好地反映岩土材料强度特性而在岩土工程中得到广泛应用，但在π平面上图形为不等角六边形，存在尖点，给数值计算带来极大的不方便。为此，前人进行了大量的修改。Drucker-Prager屈服准则是基于Mohr-Coulomb强度理论的修正准则，它在π平面上为圆形(见图4)，主应力空间的屈服面为光滑圆锥，这给数值计算带来了极大的方便，因此在数值计算中获得了广泛的应用。该准则在1952年由Drucker-Prager在Mises强度条件的基础上，考虑平均应力p或I1后提出，表达式如下:

式中:I1为第一应力不变量;J2为第二偏应力不变量。经过不断推导发展，得出不同受力条件下(即不同的 θσ)的 α，k 值，即 DP1 ～DP5［8］。

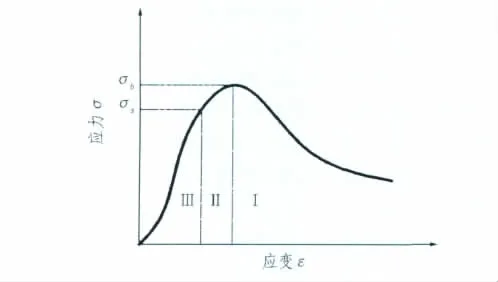
图1 岩石应力应变曲线Fig.1 Stress-strain of rock mass

岩体塑性破坏是一个过程，开挖引起应力重分布而使围岩应力不断调整，经历屈服的阶段才能达到破坏，所以屈服面不断发展直至破坏为止。本文假定破坏和屈服面形状相似，大小不同，即屈服条件和破坏条件相似［9］，都满足式(2)，只是常数项数值不同。对应于图1，相应的分区准则如下:

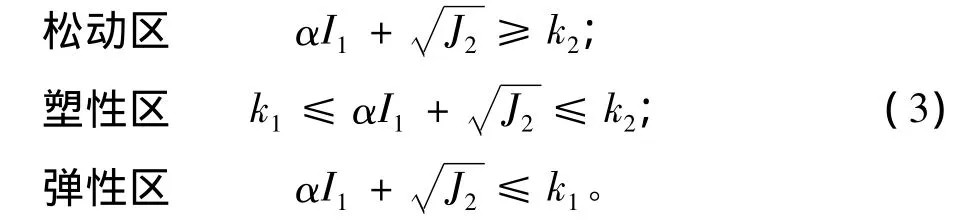
对于单向压缩和常规三轴压缩等满足σ1＞σ2=σ3条件的应力状态(DP1)，θσ=30°，此时 α =2sin φ/［(3－sin φ)］。若以单轴压缩试验来确定ki值，此时，分别以 σ1=σs或 σb，σ2=σ3=0代入式(2)，则有

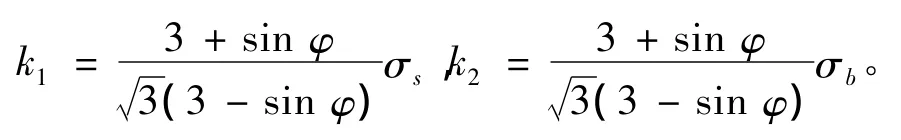
式中:σs，σb分别为岩石的屈服强度、抗压(峰值)强度。本文所提分区准则在π平面上图形如图4所示。

2 算例

2.1 有限元模型的建立

某隧道设计时速v=80 km/h，隧道断面形状为坦五心圆，开挖断面最大宽度B=10.5 m，洞高h=8.63 m，最大埋深349 m。分别选取浅埋Ⅲ级围岩(埋深H=130～270 m，13～27B)和深埋Ⅱ级围岩(埋深H=270～350 m，即27～34B)进行分析。

有限元分析软件采用ANSYS，模型如图5所示。隧道计算区域xyz=84 m×84 m×10 m，模型边界x方向位移面约束，z方向位移面约束，底部边界y方向位移面约束。隧道物理力学参数如表1所示。

图5 三维计算模型Fig.5 3D simulation model

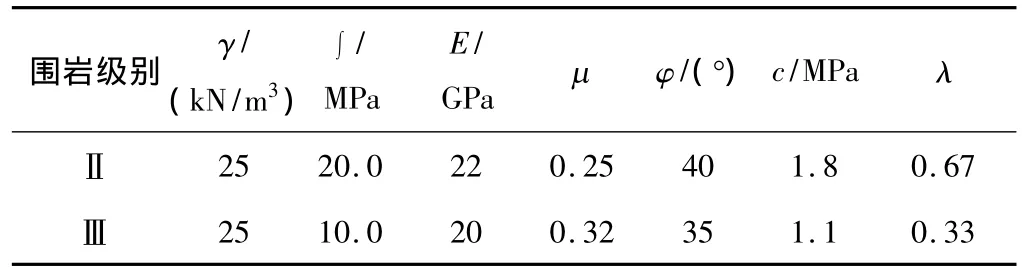
表1 岩体力学参数Table 1 Parameters of rocks

2.2 计算结果分析

本文所提分区准则实际是一种应力组合，但ANSYS软件并不能直接输出应力组合值，它支持表格运算，可用 ETABLE［10］命令将 σ1，σ2，σ3制成表格，通过表格计算命令函数(如加运算SADD，幂运算 SEXP等)，获得应力组合值αI1+结果，最后将组合结果以指定的等值线显示(本文以k1，k2区分3个区域分界)，即可明显地看到围岩分区。选择满足松动区应力组合值范围各单元，通过NLIST命令即可输出松动区范围内各节点坐标，求取包络半径即为松动区半径Rc，其计算方法如图6所示。

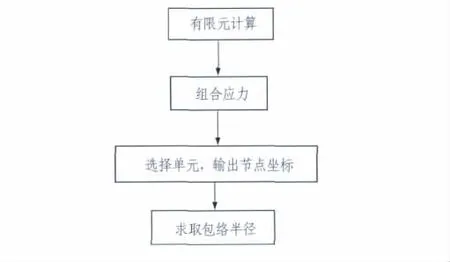
图6 松动区计算方法Fig.6 Calculation method of broken zone

同理可以得出塑性区半径Rp，而松动区厚度Rc'为松动区半径Rc与隧道开挖半径R0的差值，相应地塑性区厚度Rp'=Rp－R0。在垂直隧道轴线的xy平面，其松动区(受压屈服)半径随埋深发展过程如图7所示。图中，蓝色区域为松动区，红色部分为塑性区，其余部分为弹性区。在隧道开挖阶段，洞周附近围岩应力重分布，由于应力集中，仰拱脚部首先屈服、破碎，之后逐渐向边墙发展。对于浅埋的Ⅲ级围岩，松动区约在H=13B时开始出现，此时，其塑性区范围较小，主要集中于仰拱脚部，沿洞周边缘分布，如图7(a)所示。随着埋深的增加，塑性区形状呈现完整“侧耳形”，如图7(b)所示。对于深埋的Ⅱ级围岩，松动区发展过程与Ⅲ级围岩类似，但并非首先出现在边墙边缘，而是在离边缘一定距离的区域内，并逐渐向边缘发展，直至隧道洞周边缘，塑性区呈“羊角形”，如图7(c)、(d)所示，主要是由于在岩体深处出现了一个应力增高区，这已为很多监测所证实［2，11］。

图7 松动区随埋深发展过程Fig.7 Development of broken zone

松动区半径和埋深关系曲线如图8所示，图中Rpm，Rpm'分别为不考虑衬砌作用时由芬纳公式确定的塑性区半径及其厚度。Ⅱ、Ⅲ级围岩中的深埋隧道存在松动区，故其围岩压力可近似看作松散荷载，垂直荷载高度

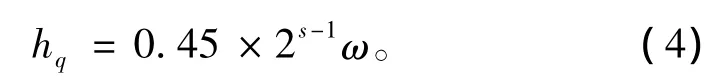
式中:s为围岩级别;ω为宽度修正系数，ω=1+i(B－5);i为每增减1 m时围岩压力增减率，以B=5 m的围岩垂直均布压力为准，当 B＜5 m时，取i=0.2，当B ＞5 m 时，取 i=0.1。

Rp，Rc与埋深H近似呈线性关系，但当埋深超过某一临界埋深时(Ⅲ级围岩H≥24 B)，松动区迅速发展而呈现指数型增长;同时，Rc'趋向于按规范求取的荷载高度hq;脚部松动区迅速发展，但速度和数值均小于边墙;岩石强度越大，松动区发展越缓慢。

现行《公路隧道设计规范》垂直荷载高度hq是根据我国411座铁路隧道施工塌方资料进行统计分析后提出的，对深埋隧道，尚未计入埋深的作用。本文计算表明，松动区半径Rc'近似呈线性趋向于hq，说明本文计算方法是正确和可信的，可与实测值对比。

与芬纳公式比较，塑性区厚度Rp'与Rpm'走向基本一致。埋深较浅时，二者误差较大，且由芬纳公式确定的塑性区偏小，主要是由于二者计算断面形状、受力状态和采取的屈服准则不同造成的，随着埋深的增加，二者受力状态越接近，差别越小。

图8 各半径与埋深关系曲线Fig.8 Relationship between radius and depth

3 结论与讨论

1)深埋隧道中，松动区分布形态及范围随埋深不同而呈现明显差异。强度小的岩体松动区大，强度大的岩体松动区小。隧道破坏以压碎破坏为主，由仰拱拱脚逐渐向边墙发展，隧道断面因其良好的受压特性而使得拉应力区只在仰拱拱顶极小范围内出现，若取岩体抗拉强度为其抗压强度的1/16，则几乎不会发生拉裂破坏。

2)随着埋深增加，Rp'与Rc'差值越来越大。这说明洞周更多的岩体进入塑性状态，塑性区扩大速度较松动区发展快。当围岩力学性能较差，Rp'随垂直地应力的增加而呈指数增长，开挖隧道时，必须注意尽早施作二次衬砌，且锚杆需局部加密或加长。

3)松动区、塑性区范围对确定荷载大小、隧道围岩稳定性分析、合理的支护措施以及开挖方案具有一定的指导意义。

4)本文假定岩体为均质的、各向同性的理想弹塑性材料，未考虑围岩破坏后物理参数显著降低的影响;同时，也未考虑结构面、裂隙等的影响。因此，本文的解是近似解。

［1］ 王梦恕.中国铁路、隧道与地下空间发展概况［J］.隧道建设，2010，30(4):351 － 362.(WANG Mengshu.An overview of development railways，tunnels and underground works in China［J］.Tunnel Construction，2010，30(4):351 －362.(in Chinese))

［2］ 曾亚武.地下结构设计模型［M］.武汉:武汉大学出版社，2006.

［3］ 邹红英，肖明.地下洞室开挖松动圈评估方法研究［J］.岩石力学与工程学报，2010，29(3):513－519.(ZOU hongying，XIAO Ming.Study of methodology for assessment of excavation disturbed zone of underground caverns［J］.Chinese Journal of Rock Mechanics and Engineering，2010，29(3):513 －519.(in Chinese))

［4］ 蒋斌松，张强，贺永年，等.深部圆形巷道破裂围岩的弹塑性分析［J］.岩石力学与工程学报，2007，26(5):983－986.(JIANG Binsong，ZHANG Qiang，HE Yongnian，et al.Elastoplastic analysis of cracked surrounding rocks in deep circular openings［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26(5):983 － 986.(in Chinese))

［5］ 周志华，叶洲元，段瑜.软岩巷道围岩松动圈的数值模拟［J］.中国矿业，2009，18(10):97 － 99.(ZHOU Zhihua，YE Zhouyuan，DUAN Yu.Numerical simulation of the broken zone in soft rock roads［J］.China Mining Magazine，2009，18(10):97 －99.(in Chinese))

［6］ 刘刚，宋宏伟.煤巷围岩松动圈规律研究［J］.煤炭学报，2002，27(1):32 － 35.(LIU Gang，SONG Hongwei.Study on the distribution law of the broken rock zone around rectangular-shape coal roadway［J］.Journal of China Coal Society，2002，27(1):32 －35.(in Chinese))

［7］ 靳晓光，李晓红.高地应力区深埋隧道三维应力场数值模拟［J］.重庆大学学报:自然科学版，2007，30(6):97 －101.(JIN Xiaoguang，LI Xiaohong.Numerical modeling of three-dimension stress field in deep tunnel of high geo-stress area［J］.Journal of Chongqing University:Natural Science E-dition，2007，30(6):97 －101.(in Chinese))

［8］ 邓楚键，何国杰，郑颖人.基于M-C准则的D-P系列准则在岩土工程中的应用研究［J］.岩土工程学报，2006，28(6):735 － 739.(DENG Chujian，HE Guojie，ZHENG Yingren.Studies on Drucker-Prager yield criterions based on M-C yield criterion and application in geotechnical engineering［J］.Chinese Journal of Geotechnical Engineering，2006，28(6):735 －739.(in Chinese))

［9］ 郑颖人，沈珠江，龚晓南.广义塑性力学－岩土塑性力学原理［M］.北京:中国建筑工业出版社，2002.(ZHENG Yingren，SHEN Zhujiang，GONG Xiaonan.Generalized plastic mechanics-The principles of geotechnical plastic mechanics［M］.Beijing:China Architecture and Building Press，2002.(in Chinese))

［10］ 王新敏.ANSYS工程结构数值分析［M］.北京:人民交通出版社，2007.

［11］ 刘宁，张春生，陈祥荣，等.深埋隧洞开挖围岩应力演化过程监测及特征研究［J］.岩石力学与工程学报，2011，30(9):1729 － 1737.(LIU Ning，ZHANG Chunsheng，CHEN Xiangrong，et al.Monitoring and characteristics study of stress evolution of surrounding rock during deep tunnel excavation［J］.Chinese Journal of Rock Mechanics and Engineering，2011，30(9):1729 － 1737.(in Chinese ))