基于Matlab的分岔理论互动式教学设计
2012-06-21胡文
胡 文
(南京航空航天大学信息科学与技术学院,江苏 南京 210016)
混沌与分形是近年来发展迅速的热门研究方向,几乎涉及理工科各个研究领域[1,2]。“混沌与分形”是我校研究生的一门选修课,主要面向电类专业学生开设。分岔理论在“混沌与分形”课程中占有非常重要的地位,是理解和分析动力系统进入混沌的关键工具。它主要研究随参数改变,动力系统解的变化[3]。分岔理论涉及较多抽象的数学概念,仅通过课堂讲解及图示介绍,学生难以深刻理解分岔理论方面的概念。
笔者通过引导学生在课堂参与调试Matlab程序,直观的了解平衡点的稳定性和非线性系统的线性化和分岔等关键概念,可以加深学生对于分岔理论的理解[4,5]。
1 分岔理论教学要点
分岔理论是对动力系统解的定性变化或拓扑结构改变的数学研究。分岔理论不仅是研究动力系统中动力学特征和现象的主要工具,也影响着对动力系统产生混沌现象的理解。
动力系统中所见到的分岔是当系统参数平滑缓慢改变时,系统发生拓扑结构上的突变。分岔类型有局部分岔和全局分岔,其中局部分岔可以由简单的程序直观描述,是课堂讲授的重点。
局部分岔与平衡点、平衡点类型和平衡点稳定性等概念紧密相连,需要先给学生讲授上述概念。对平衡点和平衡点类型的讲授,要利用相空间和解轨迹来进行演示,授课中应对这两个概念作详细说明。平衡点稳定性的分析涉及雅可比矩阵和它的特征值,授课中需复习这两个概念。
分岔可以在连续系统或离散系统中出现。在连续系统中,局部分岔发生在平衡点的雅可比矩阵特征值实部为0处,如果特征值为0就是稳定状态分岔,如果特征值为纯虚数就称为Hopf分岔。在离散系统中,分岔发生在平衡点具有模为1的特征值处,如果这个特征值等于1是鞍结点分岔、穿越分岔或Pitchfork分岔,如果特征值等于-1是倍周期分岔或Hopf分岔。在分岔理论的课程学习中,要求透彻理解连续和离散系统中常见的局部分岔概念。
分岔理论的教学中的上述概念较为抽象和枯燥,但都可以找到一些例子由简单的Matlab程序演示。鉴于大多数研究生已接触过Matlab,完全有能力理解、编写和调试简单的Matlab程序。因此,在课堂讲授分岔理论概念的同时,让学生参与现场编写调试演示程序,能使学生加深理解。演示程序调试的结果,也是教师判断学生是否理解相关概念的依据。
2 用Matlab进行互动式分岔分析
2.1 平衡点的类型和稳定性
我们授课时,借助于了Matlab中的ode45函数,讲解平衡点的类型和稳定性。
[例1]采用ode45函数来演示源、汇和鞍点这三种平衡点性质,用来演示的二维线性连续系统为
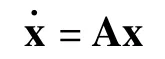
其中,x∊R2,A为2×2的常系数矩阵。上式在原点处有唯一的平衡点,在以原点为圆心的单位园上的均匀取8个点为初始值。得到8条解的轨迹在相空间中画出,可以直观看到原点处平衡点对附件初始值的吸引或排斥特性。
Matlab程序运行结果如图1(a)所示,改变矩阵的取值为
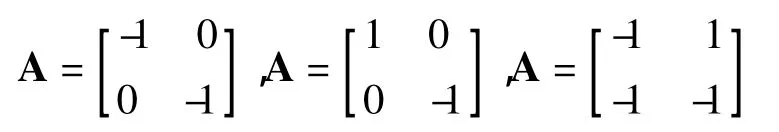
由此可以得到图1(b)、图1(c)和图1(d)的结果。从图1(a)和图1(b)中可以看到,当矩阵A对角线上的系数全为正时原点处平衡点排斥所有方向的初始值,是不稳定平衡点,称为源。反之则吸引所有方向的初始值,是稳定平衡点,称为结点或汇。从图1(c)可以看出,从单位圆上的初始值出发的轨迹,在x1方向上受到吸引,在x2方向上受到排斥。对比图1(b)和图1(d),所有方向上的初始值都受到吸引,不同的只是图1(d)中的轨迹在收敛到原点的同时还要转动,因此平衡点对附近初始值的吸引作用只受对角线上系数的影响。
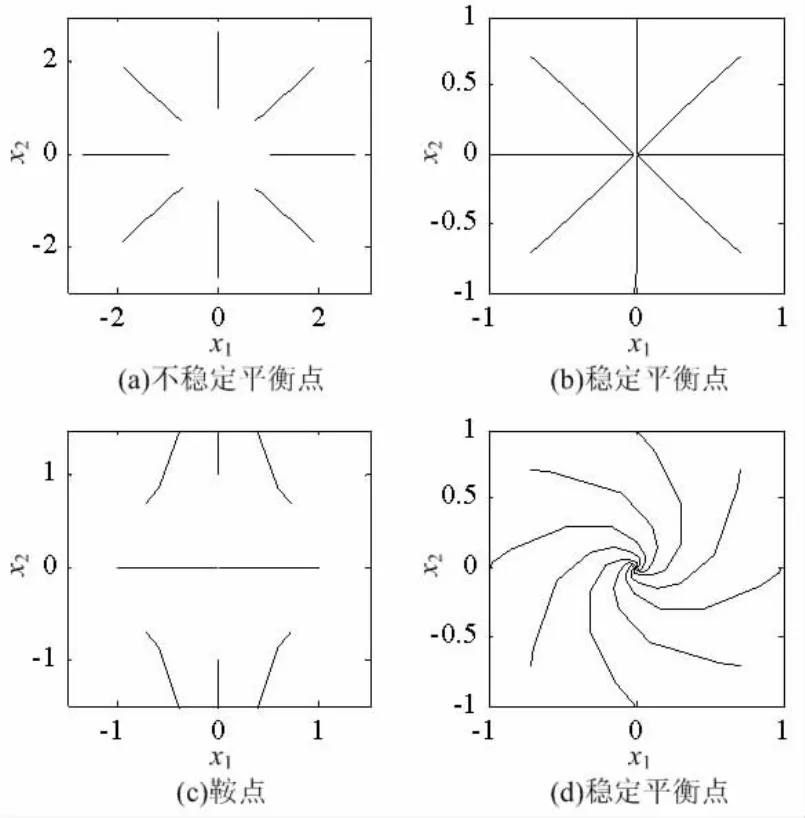
图1 系数矩阵A取不同值时初始值的轨迹
作完上述演示后,让学生动手任意改变矩阵A的系数,观察平衡点特性的变化,使其对矩阵A对角线上系数的影响将有较深刻的体会。再通过讨论,引导学生认识到对角线上的系数就是矩阵A的特征值,从容易理解线性系统平衡点的稳定性由系数矩阵特征值的实部决定这一概念。
2.2 非线性系统的线性化
在理解线性系统的基础上进一步讨论非线性系统,通过复习雅可比矩阵的概念阐述非线性系统的线性化系统,从而可以将学生对线性系统平衡点稳定性的理解扩展到非线性系统。借助Matlab中的Jacobian函数可以容易的计算任意非线性函数的雅可比矩阵。相关的主要程序分为三部分,第一部分为利用Jacobian函数得到非线性系统的线性化系统,后两部分利用ode45函数计算非线性系统解的轨迹与线性化系统解的轨迹。
[例2]采用Jacobian函数计算非线性函数的雅可比矩阵,源程序为

程序中变量dx表示一个二维非线性函数,两个变量分别是x1和x2。按需要也可以将dx改为其他的非线性函数。
介绍Jacobian函数的调用方式后,结合例1中ode45函数,学生已经可以自己动手编写演示程序的后两部分,对比线性化系统与非线性系统间的轨迹。对比程序的现场编写调试,可加深学生对非线性系统可以用线性化系统在平衡点附近逼近的理解,其中线性化系统的系数矩阵就是非线性系统的雅可比矩阵。结合例1的结果,学生能较深刻的理解非线性系统平衡点的性质将由雅可比矩阵特征值的实部决定。
2.3 局部分岔
[例3]利用Matlab中的solve函数可以得到动力系统平衡点的值,然后由Jacobian函数得到平衡点上的雅可比矩阵,再由eig函数得到特征值。这三个函数相互配合可以容易的分析动力系统的局部分岔(源程序略)。
图2(a)是程序运行的结果,可以看到当a=0,系统在原点处有唯一的平衡点,由学生动手计算该点的特征值证实该平衡点为鞍结点。随着a增大到a>0,系统产生了两个平衡点,一个为鞍点,一个为结点,两个平衡点的位置随着a的增大在x1方向上移动。由学生动手,在平衡点附近取初始值,利用ode45函数计算a=0和a=0.5时系统的轨迹。在图2(b)和图2(c)中,直观证实系统特性在a=0处发生了改变。在图2(d)和图2(e)中,逐渐减小a的值接近于0,系统状态也将越来越接近a=0时,说明这是一种局部分岔。这个互动演示的过程能使学生对鞍结点分岔概念有更清晰的认识。类似地改变源程序中的dx变量分析其他非线性系统,让学生进一步讨论和理解其他的局部分岔类型,可以全面地理解各种类型局部分岔的概念。
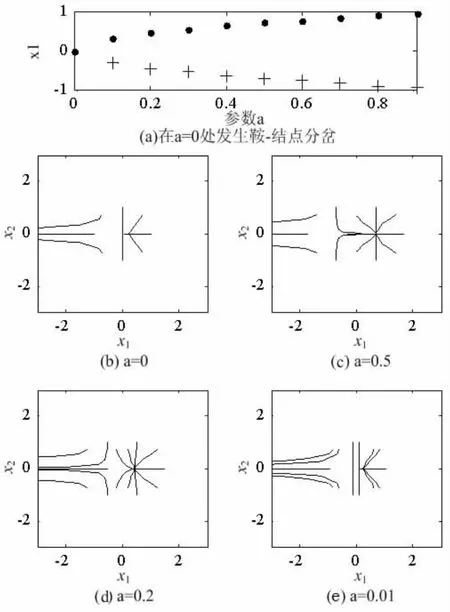
图2 鞍结点分岔
3 结语
在“混沌和分形”的分岔理论课程的教学中,我们充分利用Matlab软件工具进行互动式辅助教学。结果表明,这种引导学生参与的演示教学形式,能将抽象概念具体化、形象化和可视化,使他们在动手参与中理解枯燥的理论概念,对教学效果和教学水平的提高也大有裨益。
[1]H.O.Peitgen,H.Jurgens,D.Saupe.Chaos and fractals:New Frontiers of Science(Second edition).New York:Springer-Verlag,Incorporated,2004
[2]R.C.Robinson.An introduction to dynamical systems:Continuous and Discrete.Upper Saddle River,New Jersey:Prentice Hall,2005
[3]P.Blanchard,R.L.Devaney,G.R.Hall.Differential Equations.Pacific Grove,CA:Brooks/Cole Publishing,2006
[4]黄红飞.Matlab下DCT变换在信号压缩中的应用[J].南京:电气电子教学学报,2007(2)
[5]张萌,武攀.基于Matlab的多采样率信号处理教学设计[J].南京:电气电子教学学报,2009(4)
