基于趋势信息的电力系统负荷预测

王金行，于强强，赵生传，刘远龙，龚文杰，李文升，于大洋

（1.青岛供电公司，山东 青岛 266002；2.山东大学电气工程学院，山东 济南 250061）

0 引言

电力系统负荷预测是根据系统运行的特性、社会影响与自然条件等各种因素，在达到一定精度的条件下，确定未来某待预测时刻的负荷值大小[1]。商业负荷的特点是覆盖区域广，并且用电过程平稳，很少有大的波动，但是商业负荷具有明显的季节性差异。工业负荷的比重在用电构成中居于首位，不仅取决于工业用户的工作方式，而且与各行业的行业特点、季节因素都有紧密的联系，一般负荷是比较恒定的。农村负荷与工业负荷相比，受气候、季节等自然条件的影响很大，这是由农业生产的特点所决定的[2]。

电力负荷的特点是经常变化的，不但按小时变、按日变，而且按周变，按年变，同时负荷又是以天为单位不断起伏的，具有较大的周期性，负荷变化是连续的过程，一般不会出现大的跃变，但电力负荷对季节、温度、天气等是敏感的，不同的季节，不同地区的气候，以及温度的变化都会对负荷造成明显的影响。

电力负荷的特点决定了电力总负荷由四部分组成：基本正常负荷分量、天气敏感负荷分量、特别事件负荷分量和随机负荷分量[3]。

负荷预测根据目的的不同可以分为超短期、短期、中期和长期：超短期负荷预测是指未来1 h以内的负荷预测，在安全监视状态下，需要5～10 s或1～5 min的预测值，预防性控制和紧急状态处理需要10 min至1 h的预测值；短期负荷预测是指日负荷预测和周负荷预测，分别用于安排日调度计划和周调度计划，包括确定机组起停、水火电协调、联络线交换功率、负荷经济分配、水库调度和设备检修等；中期负荷预测是指月至年的负荷预测，主要是确定机组运行方式和设备大修计划等[4]；长期负荷预测是指未来3～5年甚至更长时间段内的负荷预测，主要是电网规划部门根据国民经济的发展和对电力负荷的需求，所作的电网改造和扩建工作的远景规划。

1 数学模型

假设两个相邻时刻t-1和t，并且这两个相邻时刻的负荷值分别为Lt-1和Lt，其中Lt-1为已知数据，它可以是上一步的预测结果，也可以是实际的历史数据，而Lt是待预测值。

分析Lt-1和Lt的取值并分析其值域，对L的值域做合理的状态划分。要求状态划分的区域是等分的。对划分后的状态进行编号，我们可以得到编号从1到N的自然数列。将1到N的自然数看做一个状态集合 E=｛1，2，…，N｝。 则 L 的取值就可以映射状态集合中的某个状态，用C，C=1，2，…，N 表示[5]。

根据同季节或者同类型日等约束条件，合理的取n组历史数据，每一组历史数据都只取t-1和t两个时刻的值。若将第i组数据的t-1时刻的状态值表示为Ct-1，i，则所有历史数据和已预测数据的C值都应该是已知的。由此我们可以得到两个相邻时刻t-1和t之间的状态变化C=Ct-Ct-1[6]。

n组历史数据可以得到n个ΔC。由C的性质可知，C和ΔC应该是整数。假设在这n个ΔC中取值为a（a在ΔC的值域中取值）共有j个，则同理描述为有j/n的概率取到a值。将这一概率按照a的值域升序排列，并将此数列看做一维矩阵，则得到转移矩阵F。

F表示了t-1到t时刻不同状态转移距离的概率。通过这一概率我们可以预测出待预测时刻状态转移的距离，由此来获得预测结果[7]。

2 山东电网负荷数据算例分析

基于趋势的预测方法认为，t时刻的负荷值Lt只与t-1时刻的负荷值Lt-1相关，而通过历史数据中t-1和t两个时刻数据变化趋势的分析，可以对待预测Lt相对于前一时刻Lt-1的变化趋势做出估计。

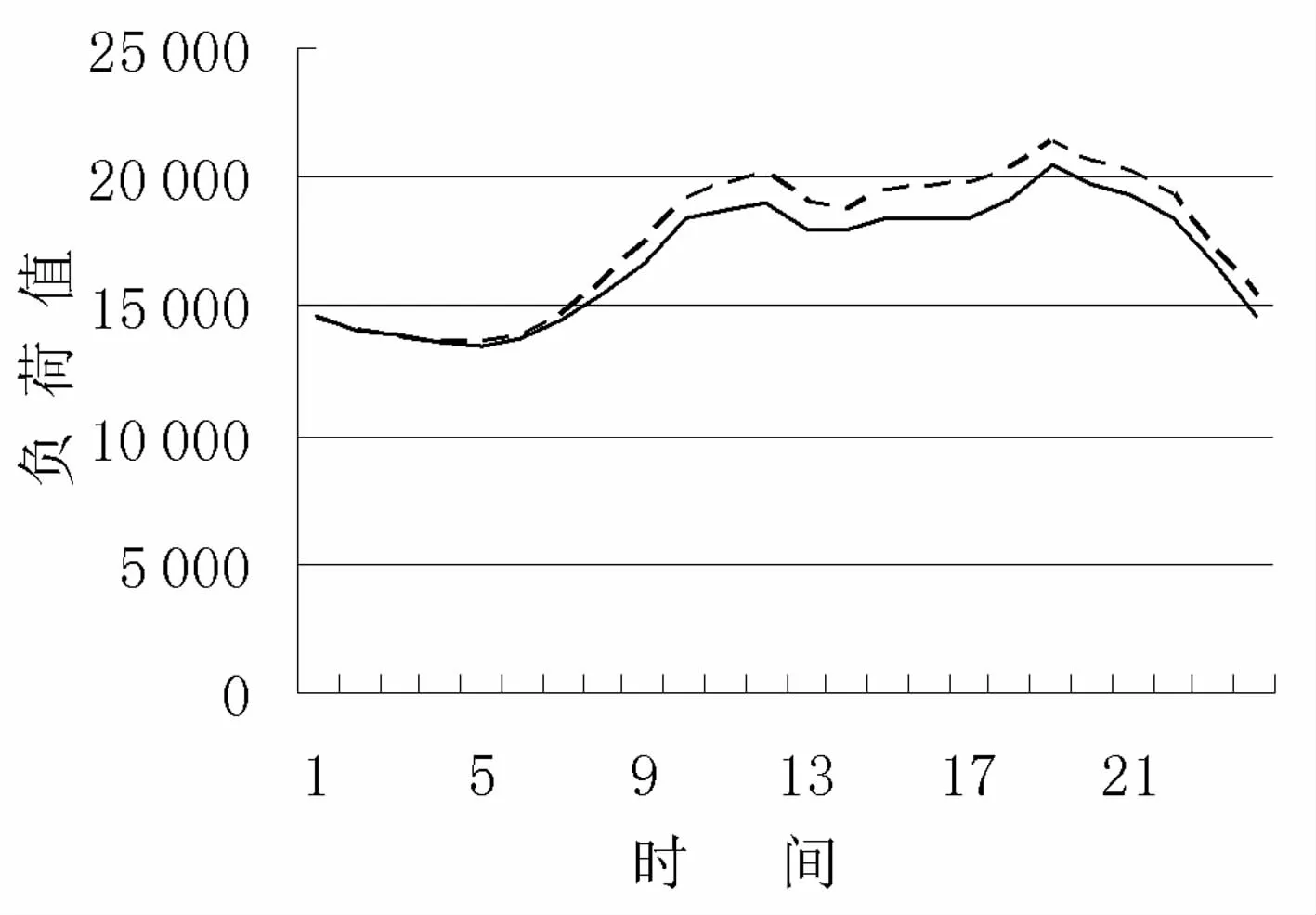
图1 山东电网统调负荷典型日数据

图1 中的实线和虚线分别表示山东电网两个相邻典型日的负荷数据。通过图1可以看出典型日的负荷数据虽然在大小上有所区别，但是却具有非常相近的趋势。虽然采集数据的典型日不同，但仍可以看出相邻两个时刻的变化趋势很相近[8-9]。

现使用实际的山东电网统调负荷数据进行算例分析。取14天t-1和t时刻的数据如表1所示。

表1 山东电网统调负荷数据

将其中第1组的t时刻数据假设为待预测数据，此时t-1时刻为已知，则预测步骤如下：

第一步，根据实际数据划定合理的状态集合。设定状态集合为 E=｛1，2，…，N｝，其中 1 状态表示负荷值为0～100之间的数值，状态表示负荷值为100～200之间的数据，依次类推。根据状态集合E可以将历史数据对应到状态量，如表2所示。

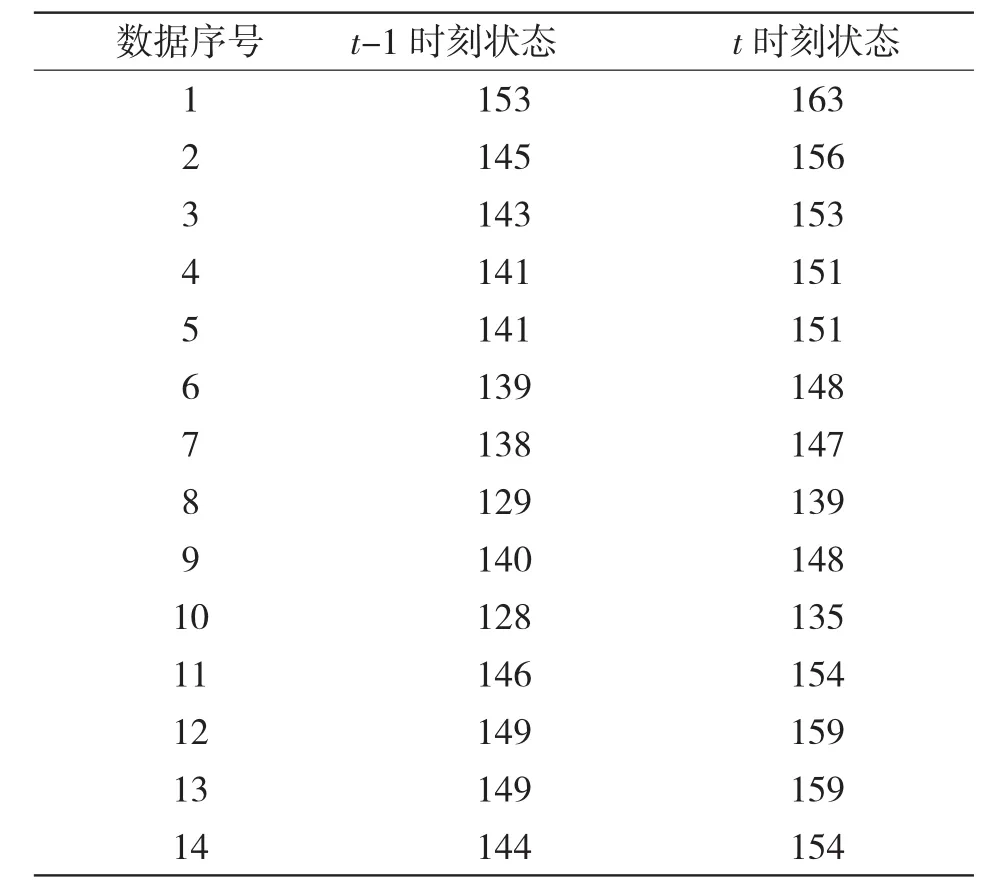
表2 历史数据对应的状态量

第二步，通过t-1和t时刻的历史数据，可以得到历史的变化趋势，即状态之间的转移距离，如表3所示。

表3 历史数据在t-1和t时刻的转移距离

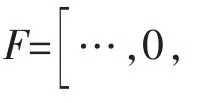
第三步，已知Lt-1所在状态为153，根据趋势预测的原则，我们可得到t时刻概率最大的状态是 163，其代表的具体数值为16 200～16 300。若要具体的数值，可以取区间中点16 250作为预测结果，并且可知此结果的概率为7/13。

第四步，利用转移矩阵F，进一步精确预测结果。有转移矩阵F的性质可知，转移距离＜+10的概率表示数据向小偏移的可能性，转移距离＞+10的概率表示数据向大偏移的可能性。

将这其概率分别相加可以得到＜+10的概率为5/13，＞+10的概率为1/13。根据转移矩阵的性质可知在区间16 200～16 300中，待预测结果偏小的可能性更大。在16 250的结果基础上，再在16 200～16 250之间取中点，得到预测结果16 225。

3 结果分析

从图1中可以看出，负荷曲线有着较强的同趋性，特别是相邻几天或者相邻的同类型日，这种同趋性更加的明显。对比算例中的历史数据，可知在相邻的t-1和t时刻历史数据所体现出的变化趋势非常一致。

分析基于趋势的负荷预测所得到的结果，只考虑最大概率转移距离时，所得到的结果是状态所表示的区间，取其中点得到预测结果，分析预测结果知其误差率在0.24%。利用转移矩阵其它结果，可以分析出预测数据偏移中点的趋势，得到修正后的结果，分析其误差率在0.08%。

4 结论

从以上算例可以看出，对于变化趋势较稳定的两个相邻时刻，基于趋势的预测方法可以进行比较高精度的预测，通过概率修正后的预测结果则可以更加精确。

本方法在运算中只要求少量的历史数据，可以有效的提高运算效率，并且可以得到概率预测结果。