SVM核函数对分类精度影响的研究①
2012-06-14刘大宁杨永乐
刘大宁, 杨永乐, 白 林
(成都理工大学管理科学学院,四川成都 610059)
0 引言
支持向量机是建立在统计学习理论的VC维理论和结构风险最小原理基础上,根据有限的样本信息在模型的复杂性和学习能力之间寻求最佳折中的方法[1].支持向量机的优点主要有:(1)SVM是专门针对有限样本情况的,其目标是得到现有信息下的最优解而不仅仅是样本数趋于无穷大时的最优值;(2)SVM最终将转化成为一个二次型寻优问题,从理论上说,得到的将是全局最优点,解决了在神经网络方法中无法避免的局部极值问题;(3)SVM将实际问题通过非线性变换转换到高维的特征空间,在高维空间中构造线性判别函数来实现原空间中的非线性判别函数,特殊性质能保证SVM有较好的推广能力,同时它巧妙地解决了维数问题,其算法复杂度与样本维数无关[2].通过计算机对比实验得到两个方面因素,它们对分类精度的影响包括:(1)核函数参数对分类精度的影响;(2)线性组合核函数对分类精度的影响.
1 SVM分类原理
SVM是从线性可分情况下的最优分类面发展而来的,最优分类面问题可以表示成如下的约束优化问题:

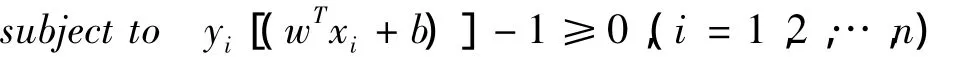
定义Lagrange函数:
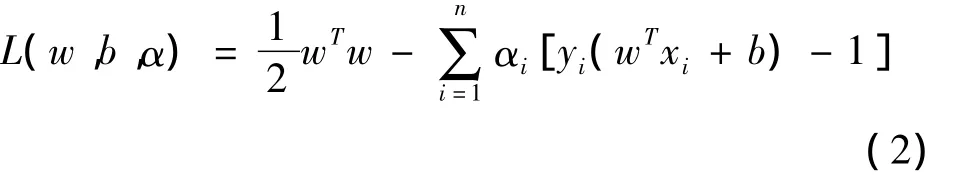
原约束条件可以把原问题转化为如下凸二次规划的对偶问题:
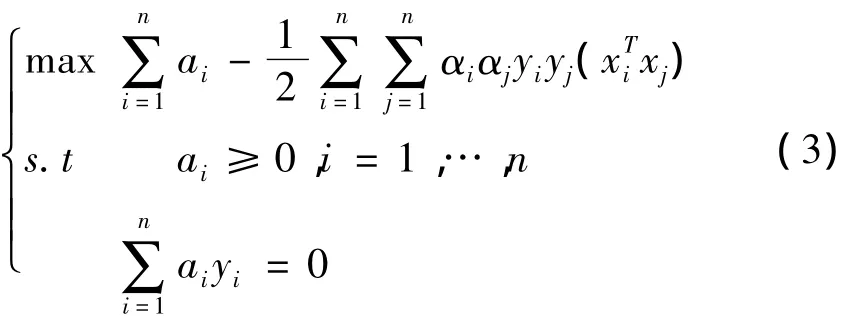
这是一个在不等式约束下的二次函数机制问题,存在唯一最优解.若ai*为最优解,则
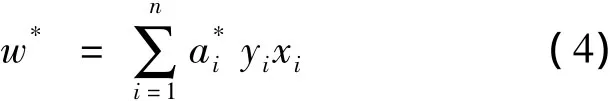
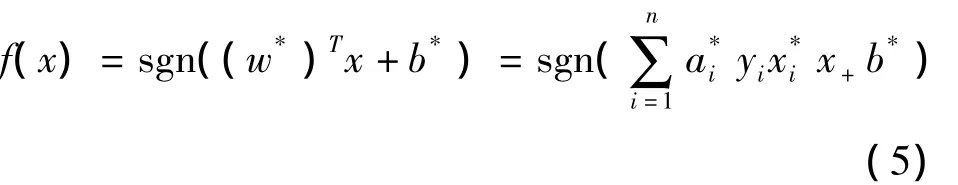
2 SVM核函数
当样本数据线性不可分时主要有两种解决方案,一种是引入松弛变量§i(§i≧0,i=1,2,...n),使超平面wTx+b=0满足yi(wTxi+b)≥1-ζi;另一种方案通过非线性变换Φ将输入空间变换到一个高维空间,然后在这个新空间中求取最优线性分类面[3].这种非线性变换是通过定义适当的核函数(内积函数)实现的,令K(xi,xj)=<Φ(xi)·Φ(xj)>取代(3)式中的
根据Hibert-Schmidt原理,只要一种运算满足Mercer条件就可以作为内积使用[5].常用于分类的核函数有以下四种:
a)线性核函数,即K(x,xi)=xTxi;对应线性可分的SVM分类器;
b)多项式形式的核函数,即K(x,xi)=[(xTxi)+1]q;对应SVM是一个q阶多项式分类器;
d)S形核函数,如K(x,xi)=tanh(v(xTxi)+c),则SVM实现的就是一个两层的感知器神经网络,对应SVM是sigmoid函数分类器[6].
根据Mercer条件,核函数的性质有封闭性、对称性、复合性.于是除了常用的四种函数外,也可以线性构造新的核函数:
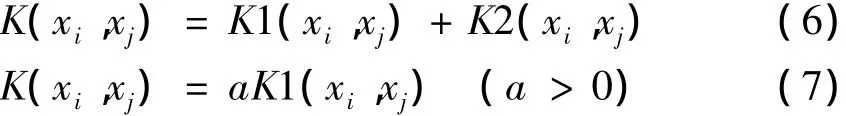
于是本文实验使用如下的组合核函数(其中核函数系数为正):
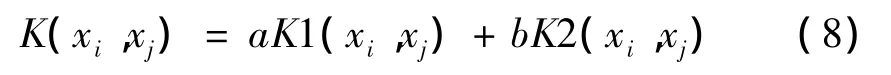
3 SVM算法实验与结果分析
本文主要考虑支持向量机分类过程中的核函数,分析了两类分类中核函数的改变或核函数对应参数的改变对分类精度的影响.实验模型的主要流程如下:
(1)选取样本点n个实验样本点,其中正类为n/2个,负类为n/2个;
(2)选择核函数类型和对应的核函数参数值;
(3)将训练样本点数据代入实验模型得出最优分类曲面;
(4)选择测试样本点m个,预测其归属类型,并与实际类别进行对比,最后获取分类精度.
实 验 中 我 们 调 用 Matlab7.11.0 下randn('state',3)状态语句,然后通过给定样本数n的大小来产生第一类二维训练样本x1=randn(n,2),赋予对应的类别为y1=ones(n,1);第二类训练样本点为x2=5+randn(n,2),赋予对应的类别为y2=-ones(n,1).
测试样本我们选取的是:tx1=1+randn(50,2),给定它们的类别为正类ty1=ones(50,1);tx2=4+randn(n,2),给定他们的类别为负类ty2=-ones(50,1).这样选用的样本点在每次实验中当样本量n不变时,随机产生的数据保持不变,当n改变时,训练样本数据仍然保持和n变化之前数据的相关性.图1为核函数为线性时,训练样本点为n=100的分类情况,训练点1和训练点2为选取的训练点,测试点1与测试点2为测试点分类情况,计算得出其分类精度为0.9700.下图1为一张样本容量为100,线性核函数分类所获取的分类模型图.
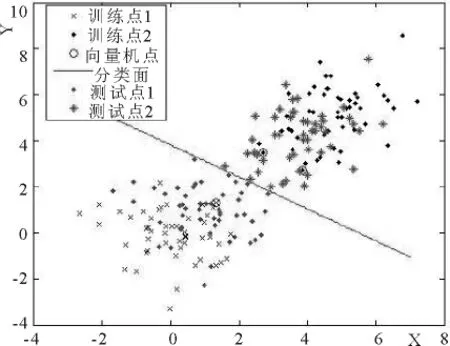
图1 样本容量为100,线性核函数分类
3.1 核函数参数对分类精度影响
本实验对如下情况进行讨论:三种核函数的参数取整数值,且样本容量为 100,200,300,400.具体获取的分类精度值如下所示:
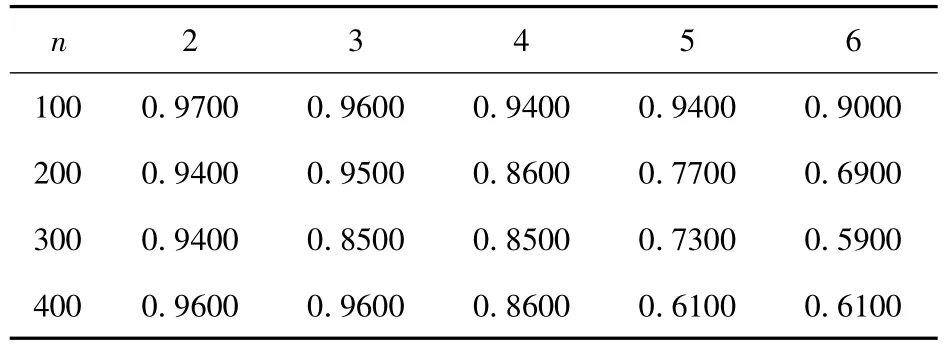
表1 不同样本下多项式核函数不同参数分类精度
由表1中实验数据可以明显看出,当样本容量为n,测试样本不变时,随着q值变化即多项式次数的变化,同一样本分类精度有明显下降趋势.因此在多项式核函数分类中,并不是多项式次数越高分类效果越好.对于该实验数据当我们选取样本量为100,多项式次数为2的核函数时,就可以达到0.9700的分类精度.
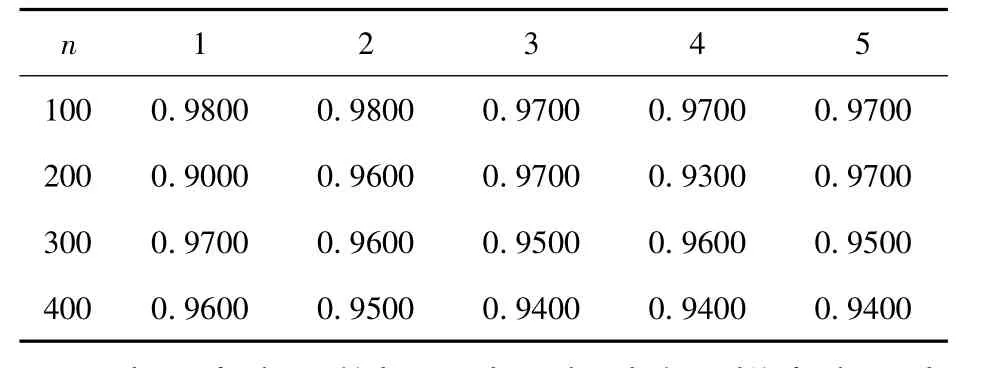
表2 不同样本下高斯核函数不同参数分类精度
表2中实验数据可以观察到除了样本容量为200,方差σ=1和4时,针对于同一方差,随着样本容量的变大,分类精度逐渐减小.当样本容量为100,高斯参数取值为1和2时,获取最优精度0.9800.
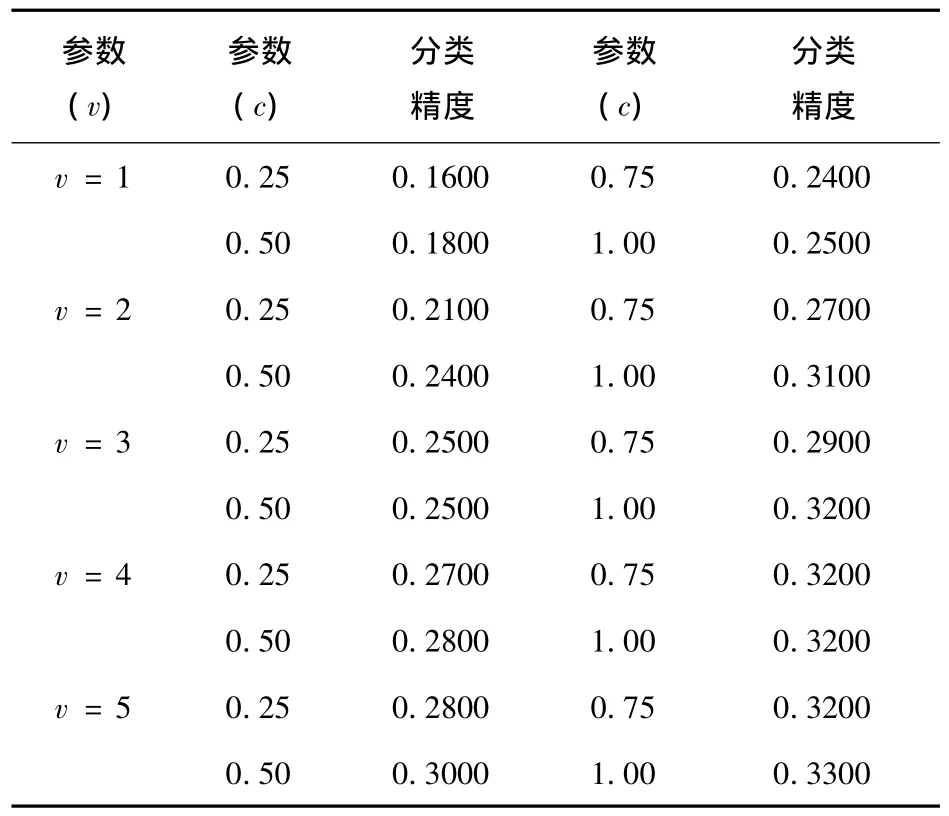
表3 不同样本下S形核函数不同参数分类精度
根据表3中实验数据,可以明显的得出结论.总体来说,在选取的区域范围内,S形核函数分类效果较差,但是分类效果的区别我们可以很明显的看出来.对于实验训练样本容量为100,采用形核函数的SVM,同一参数v,c在区间[0,1]取值得出的分类精度,将随着c的增大而提升.
3.2 组合核函数参数对分类精度影响
综合上表观察到同一核函数对于不同的训练样本数量,分类精度的变化不是很大,大致保持一致,我们不能完全得出结论说训练样本越大则分类精度越高,或者训练样本越小则分类精度高.于是想到通过组合核函数进行实验(其中m与k为两类核函数,它们的线性关系分别对应式(11)中的a与b),实验中为了观察组合核函数与单独核函数的差别,在选取m与k的值时我们保持m+k=1,对比实验数据如下表.
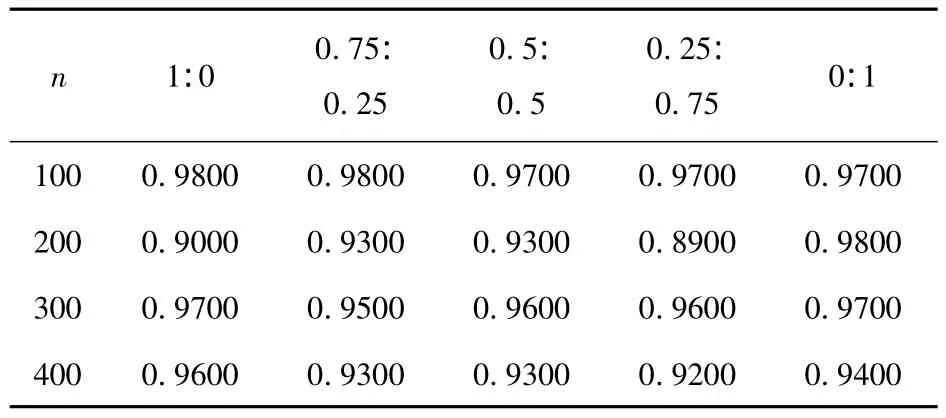
表4 组合核函数1(高斯核函数(σ=1)与线性核函数)
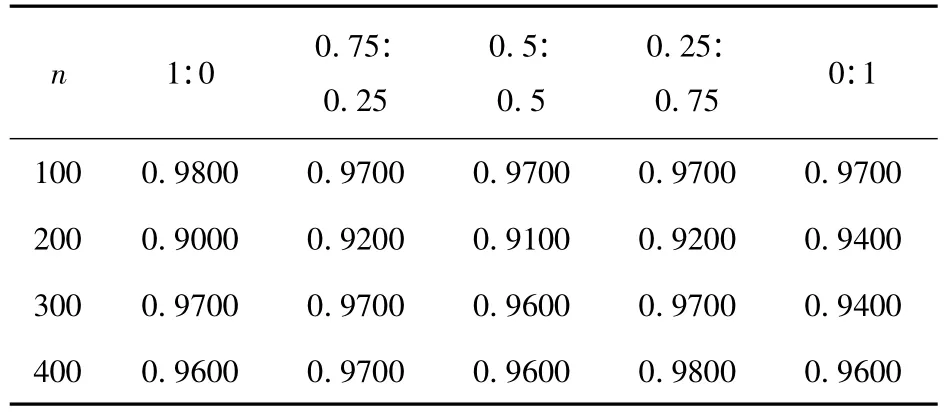
表5 组合核函数2高斯(σ=1)与多项式组合核(q=2)函数)
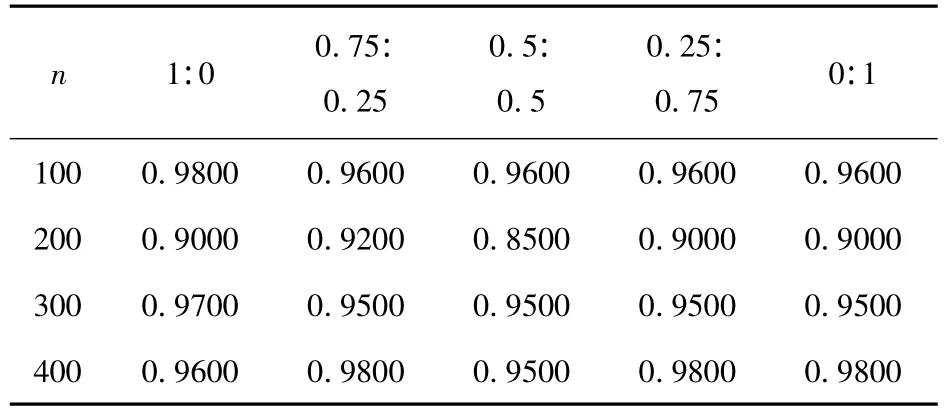
表6 组合核函数3(高斯(σ=1)与多项式组合核(q=3)函数)
分析三组实验数据,组合核函数1中高斯函数(σ=1)与线性核函数各自组合前分类精度都比较好,同一训练样本以不同的比例组合核函数分类之后的分类精度,都没有同时超过各自单独作为核函数的精度,于是就本实验中的数据组合核函数1的分类精度是不够优的;组合核函数2中样本容量为400,m:k=0.5:0.5 时,分类精度取得了 0.9800,比高斯(σ=1)核函数获得的分类精度0.9600和多项式(q=2)核函数获得的分类精度0.9600都要高出0.02个精度;组合核函数3中单个样本容量n=100,m:k=0.75:0.25 时,分类精度取得了0.9200,比高斯(σ=1)核函数获得的分类精度0.90和多项式(q=2)核函数获得的分类精度0.9000都要高0.02个精度.
总体观察我们也可以看出,组合核函数的分类精度都没有太大降低到组合之前的分类精度,通过合理的组合核函数提高分类精度.
4 结论
尽管有些实验结果表明,核函数的具体形式对分类效果的影响不大,但是通过实验可以看出核函数在SVM方法中能够起到调整参数的作用[7].核函数一般使用多项式、径向基函数等的形式,其参数的确定决定了分类器的类型和复杂程度,它显然应该作为控制分类器性能的方法[8].实验中多组对比实验得出,通过不断的筛选核函数参数可以获得更优的分类精度,同时,合理的线性组合核函数构成新的核函数在一定程度上也可以提高分类的精度.在实际应用中可以根据实验数据的特点调整核函数的参数与形式来获取最优的分类精度.
[1]Vapnik VN,著;张学工,译.统计学习理论的本质[M].北京:清华大学出版社,2000,293-322.
[2]Nello Cristianini,JohnShawe- Taylor,著;李国正,王猛,曾华军,译.支持向量机导论[M].北京:电子工业出版社,2004,103-245.
[3]郭光绪.支持向量机的缺陷及改进[J].计算机与现代化,2012,1(29),5-7.
[4]江泽坚,孙善利.泛函分析[M].北京:高等教育出版社,2005,47-70.
[5]张战成,王士同,邓赵红,等.支持向量机的一种快速分类算法[J].电子与信息学报,2011,33(9),2181-2186.
[6]顾亚祥,丁世飞.支持向量机研究进展[J].计算机科学,2011,2,38(2),14-17.
[7]祁亨年.支持向量机及其应用研究综述[J].计算机工程,2004,30(10),6-9.
[8]张睿,马建文.支持向量机在遥感数据分类中的应用新进展[J].地球科学进展,2009,5,24(5),555-561.
