多径信道下OFDM系统定时同步算法

朱琳琳，李 欣，王丽丽

（哈尔滨理工大学 通信与信息系统，黑龙江 哈尔滨 150010）

OFDM（Orthogonal Frequency Division Multiplexing）是 一种多载波调制技术，它将数字信号处理、数字调制、多载波传输等技术结合在一起。由于其能够有效地对抗无线信道多径时延扩展的影响，一直是3G通信领域的研究热点[1]。

在OFDM调制中，所有子载波保证相互正交。正是由于正交性的存在使得OFDM相对于传统串行调制以及一般多载波调制有很多优点。然而也是因为这一点，基于OFDM的系统对定时和频偏比较敏感，定时同步偏差和载波频率偏差会产生码间干扰（ISI）和载波间干扰（ICI）[2]。目前有很多文章分析了OFDM信号的定时同步问题，提出了许多解决方案。概括起来可分为两大类，一类是基于数据辅助法，指在传输过程中插入特殊的训练符号来辅助估计，以便更容易进行同步信息的提取和提高同步准确性。较典型的一种算法是Schmidl&Cox提出的基于特殊训练序列进行定时和频率联合估计的方法（SC算法）的定时频偏估计[3]，以及利用CAZAC（Constant Amplitude Zero Auto Correlation）序列作为前导进行同步的方法。第二，非数据辅助型。利用循环前缀（CP）的相关特性来估计时间同步，如Van de Beek提出的最大似然估计（ML）法和 Kenkichi提出的差分法[4]，及文献[5]中提出的差分法与集相关相结合的方法。然而，上述这些方法对于多径信道下的时间估计和频率估计的准确性是十分有限的。

文中在文献基础上提出了基于相关函数导函数约束下的规则优化的定时同步算法。该算法不仅克服了最强径不是第一根径对多径信道的影响，而且适合于大规模网络的多模终端通信，并且能够保证每一个网络进行切换时保持网络之间的粗同步。该算法可以用在多径衰落信道下，通过仿真验证具有很好的效果。

1 OFDM系统模型

在OFDM系统中，设Xk为第K个子载波上调制的基带数据，经过IFFT变换后，一个OFDM符号持续时间内发送的信号序列可以表示为：

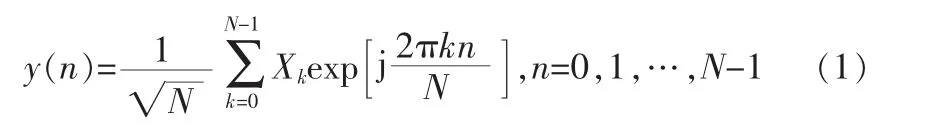
信号通过M条独立信道后，接收端接收到的信号为：

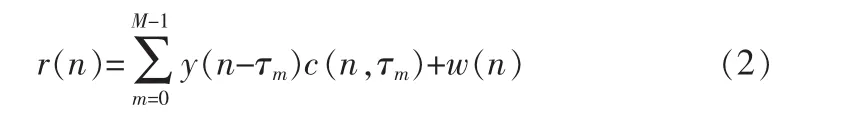
其中 w（n）为噪声，c（n，τm）为每条路径的衰落参数，对应的信道多径时延为接收到的数据。在理想情况下，不考虑多径传输、终端移动和发射端的晶振偏差时，假设信道的传输函数为h（t），其傅氏变换为H，则FFT变换后的OFDM信号为：

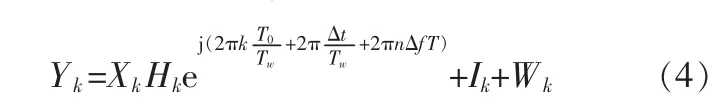
其中Wk表示信道噪声，Ik表示由于载波频偏引起的ICI，Tw是OFDM符号中有效数据的持续时间，T是采样间隔，T0是符号误差，Δt是采样率误差，Δf是载波频移。式（3）和式（4）之间的差别就是OFDM系统中不同步的现象。

其中Hk为信道响应函数在第K个子载波上的系数，Wk为噪声的FFT变换。但是考虑到无线传输信道的特点，信道具有多径传输和移动终端等特征，所以FFT的实际输出为：

2 OFDM定时同步算法

2.1 OFDM定时同步算法分析

OFDM同步算法可分为两类：pre-FFT和post-FFT算法。Pre-FFT处理的目标是为FFT处理提供给数据符号，以使ISI和ICI减至最小。否则，FFT输出指标将会下降。然而。Pre-FFT处理过程必须提供粗定时队列和细频率偏移修正。为了实现pre-FFT同步，算法将利用符号结构或者循环前缀CP[6]。对于定时估计来说，以有效的符号间隔为始发计时点是最理想的。设最大延时为τmax，数据符号长度为N，循环前缀长度为Ng，采样间隔为Ts，保护间隔为Tg。定时点可以提前CP时间为Tg-τmax。分析如果定时超前，即定时偏差在循环前缀内，那么由于循环前缀部分是符号中后面若干FFT样值点的复制，因此超前的偏差将只引起相位的旋转，并不会带来ISI和ICI，也不会带来幅值的变化，通过相位补偿即可恢复，因而也就不会引起系统信噪比性能的下降；如果定时滞后，此时定时偏差在循环前缀外，由于丢失了第i个符号中的部分信息，而且加入了第i+1个符号循环前缀中的部分信息，即解调信号属于不同的OFDM符号，所以引入了不可恢复的OFDM相邻ICI，并且可能带来一个符号内载波间正交性的破坏，进而造成了系统信噪比性能的损失[7-8]。

文献[4]提出利用循环前缀的时间频率联合同步的算法，通过计算最大函数来估计时间和频率偏差。当定时估计中插入加性高斯白噪声（AWGN），最大似然函数则包括一个总相关项和一个能量相关项（E）。 如式（5）、式（6）所示：

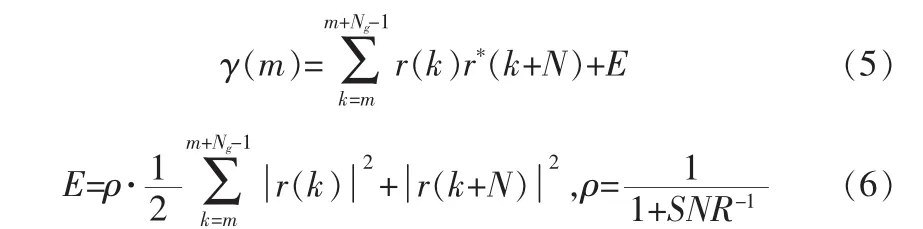
2.2 多径信道下新算法描述

本文主要利用循环前缀与其相隔N个抽样点信号之间的相关性得到定时同步估计，再利用相关函数的导数来处理估计延时。

首先，分析OFDM系统中多径信道下相关器的输出。相关函数γ（m）在AWGN信道下可以看做是一个三角函数，理想的定时点是峰值，斜坡的长度是CP的时间间隔（Tg）。多径环境下，由公式（2）得出的相关器的输出为：

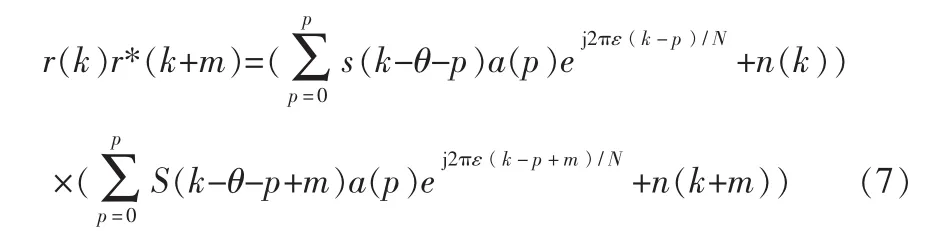
假设独立同分布符号、噪声采样、非零项的计算都在以下4 种情况下完成，即 m=0，N，N-p，N+p。除了长多径延迟外，假定其他情况不可能发生，并且忽略自动相关项，只考虑m=N的情况，其期望是：

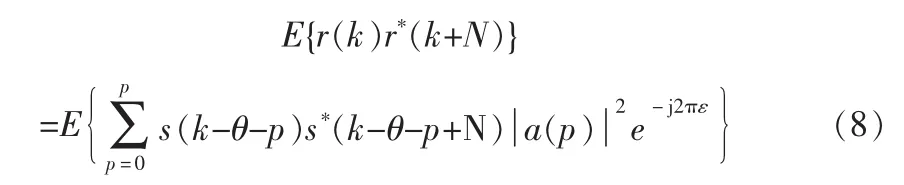
1）所有的多径分量都分给当前的符号：

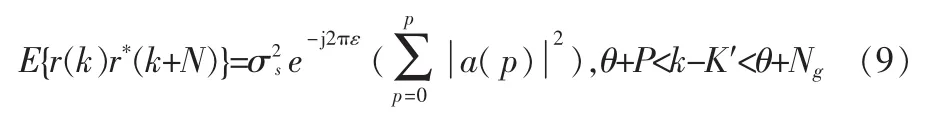
2）先前的符号在多径分量中产生长延时：

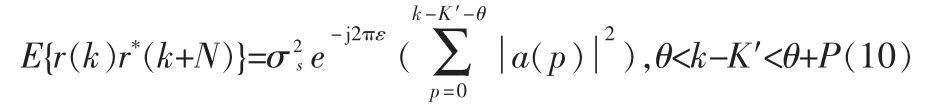
3）之后的符号在多径分量中产生短时延：

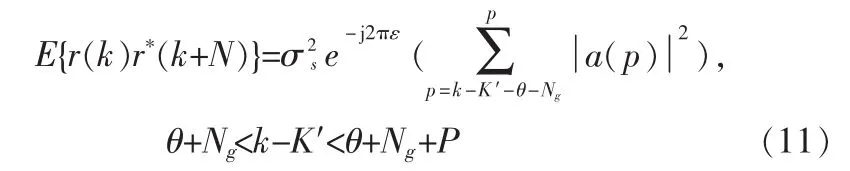
除了以上3种情况，其他期望都为0，现在考虑单个多径分量对期望的贡献，φ，表示为 Er（k，φ）。 这 3种情况（非零期望）产生如下等式：

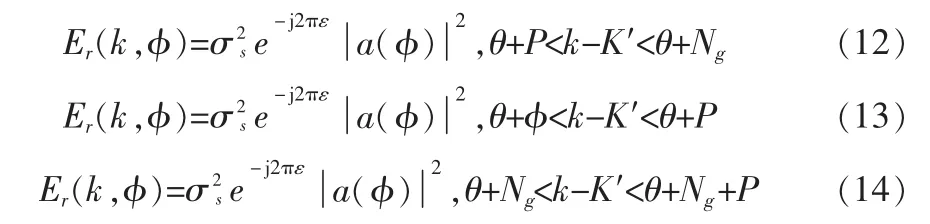
这说明每一个多径分量都需要一个三角函数，该函数的时延峰值为θ+φ。在多径信道下，γp（m）的峰值不需要指定第一条到达的路径，如图1所示。但是在这种情况下，由于定时估计延时的问题，系统内将会产生ISI，为了克服这种影响，本文利用对相关函数求导的方法来解决估计延时问题，克服系统内ISI的产生。

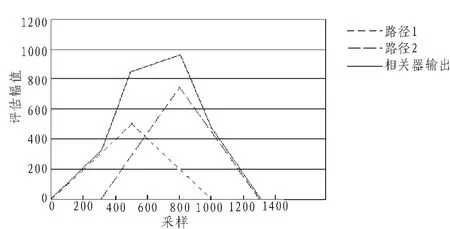
图1 两条路径相关函数的叠加Fig.1 Superposition of two paths correlation function

从图1得出，在多径环境下峰值检测表现为高估计误差。 当最大的多径延迟小于 γi（m）时，γi（m）函数将添加到每个多径组件中，并且全部增长。在第一个组件（径）峰值之后，γi（m）函数开始递减，其他的组件（径）一次停止增长，根据路径延时选择递减时间点。因此，理想的定时点是函数γp（m）的导数开始下降的时间点。图2说明了上述分析，理想定时点在512采样处。

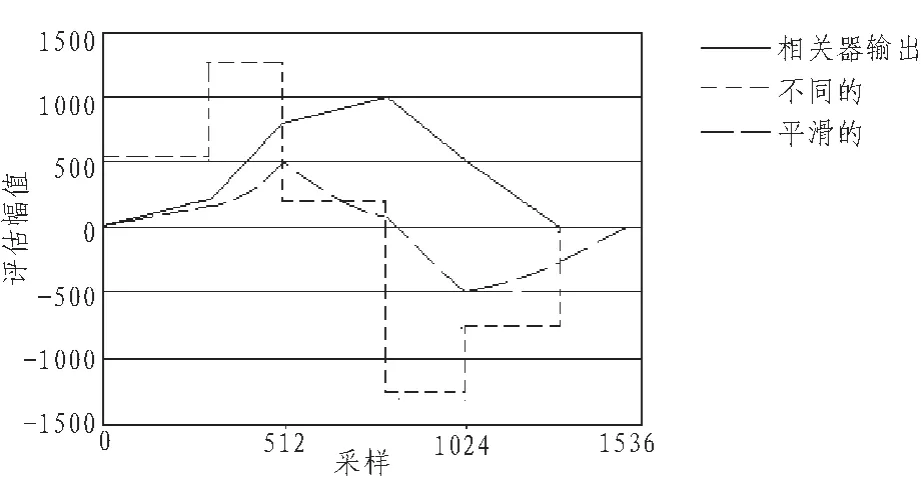
图2 相关导函数与平滑导函数Fig.2 Related to derivative and derivative smoothing

图3描述了文中的定时估计系统。以公式（3）为输入信号，设时间偏移为k，符号索引为K，则相关器的输出为：

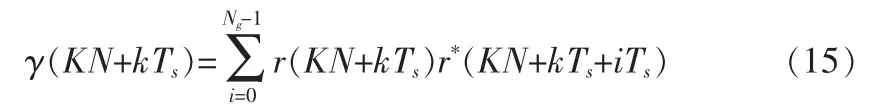
该系统通过求导获得更好的定时估计，同时不增加算法的复杂度。对于不同的CP长度，通过经验分析，当滤波长度为CP长度的一半时，定时估计比较好。对估计求导得：

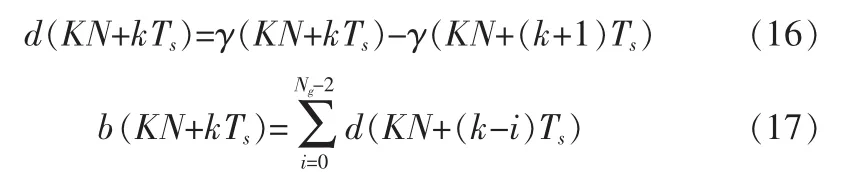
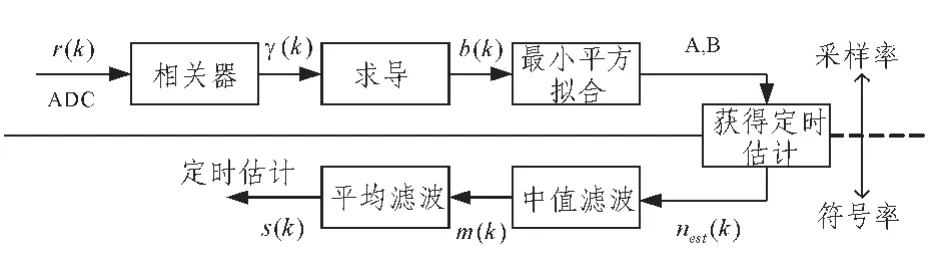
图3 定时估计系统Fig.3 Timing estimation system

文中提出的算法通过一次求导找到峰值过后的下降时间点，而在实际中，在导函数下降之前，函数会有一段平缓的部分，所以单一的峰值检测得出的结果并不会很理想。在本文中，我们采用最小平方拟合的方法来寻找下降沿。而且，我们需要根据导数峰值来设定两个门限值，使采样的下降点在这两个门限之间。门限值的设定应依据CP的长度，对于短CP（64-Points），门限值设定为导函数峰值的40%-95%。当CP长度变化时，门限值应该重新设定。该算法可以对每一个符号给出其定时估计，但是，偶尔某个同步参数的估计会产生比较大的误差，利用中波滤波可以消除这些不好的结果。

2.3 基于规则约束下的改进算法

文中提出的新算法利用了线性拟合和差补法的处理过程，该算法性能优于现存的同步技术，但是在测试中发现，其存在偶然误差。为了进一步减小估计误差，本文在相关函数和导函数基础上引入规则检测的思想，即利用相关函数和导函数的附加信息来识别不可能估计，或是利用与当前信息更加一致的信息来替换之前的信息，通过这些来减小误差。

定义 Ri（tE）为规则，其中 tE指时间估计，Li（tE）指 tE本身的约束。对于文中提出的相关函数和导函数的定时估计方法，提出以下规则：

1）定时估计不能晚于相关函数输出的峰值，定义为规则1：R1（tE）；

2）定时估计不能早于相关函数的峰值，迟于CP的长度，因为峰值一直保持在CP的时间间隔内，表示为R2（tE）；

3）定时估计不能早于导函数的峰值，因为是峰值后的极限点，表示为 R3（tE）；

4）已经确定的估计是有可能存在误差的，这种情况，我们应该用和强限制更加一致的估计或者之前的估计做替代。（替代分为3种情况：硬替换、“前”替换、“后”替换）。

图4给出了该规则检测的处理过程。

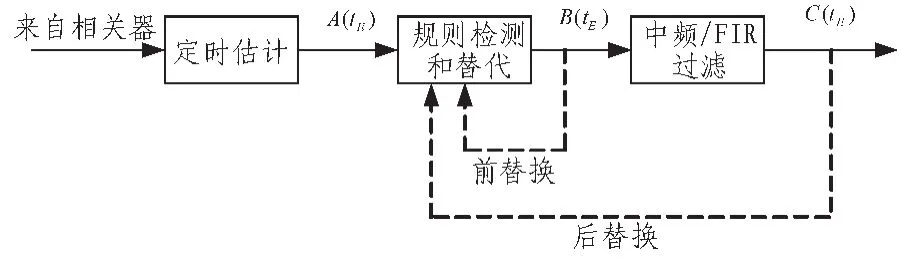
图4 规则检测处理过程Fig.4 Rule detection process

3 仿真与性能分析

为了测试提出算法的性能，文中在Matlab软件下仿真DVB-T系统。仿真在两种信道模式下进行，目的是测试算法在普通信道下和复杂信道下的表现。对于普通信道，选择2K模式，16QAM模块，CP长度为64，波长15的中频过滤器和波长16的FIR过滤器；对于复杂信道，应用了一个8-径的多径信道，每一条信道的最大时延为31个采样，其他参数设置与简单信道相同。仿真结果与Beek算法进行了对比。图5、6给出了算法在两种信道模式下信噪比与定时误差之间的关系。

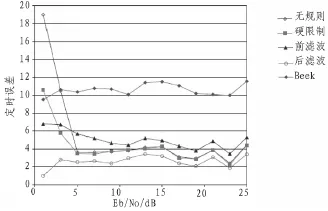
图5 简单信道下定时误差与信噪比Fig.5 Simple channel timing error and signal to noise ratio

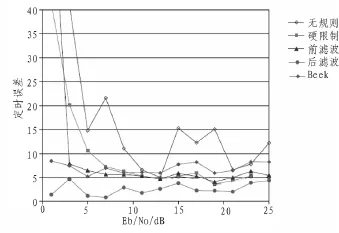
图6 复杂信道下定时误差与信噪比Fig.6 Complex channel timing error and signal to noise ratio under

从上面的结果得出，在简单和复杂信道模式下有规则约束下的算法表现要优于无规则的情况，在简单信道下，单纯的无规则约束下的算法表现也优于Beek算法，而在复杂信道下，无规则约束下算法的稳定性较差。而在简单和复杂两种信道情况下，后过滤系统表现都优于其它情况，算法稳定性也优于其它情况。

图7、8给出了在两种信道情况下系统时延对定时误差的影响。从结果中我们可以得出：在简单信道下该算法优于Beek算法，在多径信道情况下，在系统采样最大延迟超过CP长度后，在无规则约束下，算法的定时误差快速增加；在两种信道模式下，后过滤约束使得算法的表现更加完善。总体看来，基于规则的导函数和相关函数算法在处理OFDM系统定时同步上的性能表现要优于其他算法。

4 结束语

OFDM系统中定时同步的准确性将直接影响系统误码率的性能，超前的定时偏差将引起相位的旋转；滞后的定时偏差将引入不可恢复的OFDM相邻符号间干扰，并且可能带来一个符号内载波间正交性的破坏，因此将造成了系统信噪比性能的严重下降。如果在多径信道下，这种干扰将更加严重。本文提出的多径信道下OFDM定时同步算法，有效的解决了上述问题。通过Matlab仿真，该算法在定时同步方面具有很好的鲁棒性，即使在CP长度很短的情况下也能够检测到峰值，同时能够较好地估计信道各条径的时延，相比于现有的其他定时同步算法，它们的适用范围更广，估计精度更高，且实现复杂度更低。

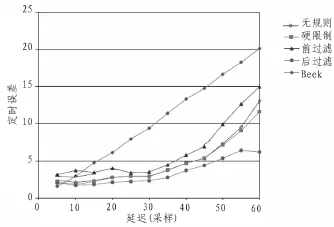
图7 简单信道下延迟对定时误差的影响Fig.7 Simple delay channel under the influence of the timing error

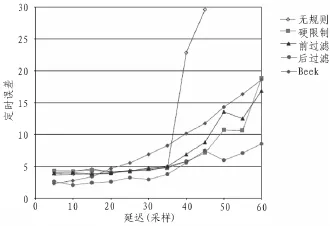
图8 复杂信道下延迟对定时误差的影响Fig.8 Complex channels delay the impact of timing error

[1]佟学俭，罗涛.OFDM移动通信技术原理与应用[M].北京:人民邮电出版社，2003.

[2]Shi K，Serpedin E.Coars frame and carrier synchronization of OFDM system:a new metric and comparison[J].IEEE Transactions on Wireless Communications，2004，3（4）:1271-1284.

[3]Schmidl T M，Cox D C.Robust frequency and timing synchronization for OFDM[J].IEE E Transactions on Communication，1997，45（2）：1613-1621.

[4]Vande Beek J J，Sandell M，Borjesson P O.ML estim ation of time and frequency offset in OFDM systems[J].IEEE Trans Signal Processing，1997，45（7）:1800-1805.

[5]Park B，Cheon H，Ko E，et al.A blind OFDM synchronization algorithm basedon cyclic correlation[J].IEEESignalProcessing Letters，2004，11（2）:83-85.

[6]Schmidl T M，Cox D C.Robust frequency and timing synchronization for OFDM[J].IEEE Transactions on Communication，1977，45（12）:1613-1621.