基于有约束最小二乘法的IQA算法曲线拟合

王学珍，刘 昱，李器宇，汪少初

(天津大学电子信息工程学院，天津 300072)

图像质量评价(Image Quality Assessment，IQA)属于信号处理学科中较为年轻的领域，分为主观评价和客观评价两种方式。主观评价方式讲究样本采样，以样本分布模拟总体分布，把参与评价的主体的平均打分作为图像质量主观评分(Mean Opinion Score，MOS)[1－3]。主观评价因为评价周期长、参与人数多、对主客观条件均要求严格，不利于在实践中推广。与之相反，客观评价方式借助高性能计算机和基于人类视觉模型的算法设计，不仅能快速给出始终一致地图像质量评分，而且方便嵌入其他工程应用[4]。近些年，研究者们对IQA客观算法的设计与改进取得了不少优秀成果。然而，针对客观算法的准确性评估一直都存在争议。

Richard Dosselmann[5]对IQA算法中获得广泛应用的结构相似度[6](Structural Similarity index，SSIM)算法与均方误差(Mean Squared Error，MSE)算法进行统计分析和主观比较研究之后发现，上述两种算法的性能有很多相近的地方。这与文献[6]和文献[7]的结论不同。此后，他与Xue Dong Yang合作[8]为SSIM算法和MSE算法的度量值建立了代数关系式，更进一步拉近了两种算法之间的关系。以上成果提供了审慎反思的新视角，它对IQA算法中仅凭少数个例，或通过缺乏可信度的统计分析而得到的结论提出了质疑。为了给不同的IQA算法做准确评估，Hamid Rahim Sheikh 等[7]和 Nikolay Ponomarenko 等[9]采取了相同的策略，他们分别设计了LIVE database图片库和TID2008图片库来代表各种图像内容和失真类型，以对应图像的MOS值作为评估IQA算法的依据。不同的是，Sheikh[7]提出首先用1个含5个参数的Logistic方程做数据的非线性回归拟合，然后选用3种性能度量指标分别做评估;不足之处在于Logistic方程缺乏普遍意义，以及3种性能指标的统计学意义含重复的部分;Nikolay Ponomarenko[9]则直接选用Spearman相关系数和Kendall相关系数对各算法分别进行排序，这2个统计指标显得过于粗糙、简陋。

视频质量专家组(Video Quality Experts Group，VQEG)作为推进视频质量评价VQA(Video Quality Assessment)，由于VQA与IQA的评估标准相同，本文中一律用IQA代替)领域的专家组织，前后推出3次针对视频质量评价算法评估的报告[1－3]。在统计分析策略方面，新报告相比之前版本均有变动。最新版本报告[1]的策略为:首先用1个保证单调递增的含4个参数的三次多项式方程做为数据的非线性回归拟合;然后选用3种性能度量指标分别从不同角度做评估。该报告未提供三次多项式方程形式的非线性回归拟合的具体实施过程。

针对VQEG提供的IQA算法评估策略中未作说明的，三次多项式形式的非线性回归拟合过程开展研究，力争探索一种客观评估IQA算法性能的方法。本文选用TID2008图片库[9]及其MOS数据作为实验素材，以峰值信噪比(PSNR，Peak Signal to Noise Radio)、SSIM[6]和多尺度 SSIM[10](MSSIM，Multi－scale SSIM)3 种算法为评估的对象举例，给出了基于有约束最小二乘法的曲线拟合过程。

1 对IQA算法的评估过程

主观评价被认为是评价图像质量最有效力、最可信赖的方式[11]。因此，本文认为对IQA算法做评估的过程就是衡量IQA算法度量值与主观评分的相似度和差异度的过程。本文仅对图像逼真度(Image Fidelity)感兴趣，因此只涉及全参考IQA算法的质量评估。其中所采用的三次多项式形式的回归映射函数和3个性能指标，均参照VQEG[1]的做法;考虑到TID2008数据库中MOS值的获取途径，原始图像(或参考图像)的MOS值存在缺失，因此，将文献[1]中出现DMOS值的位置用失真图像的MOS值代替。

1.1 回归映射函数

回归映射函数的方程形式为

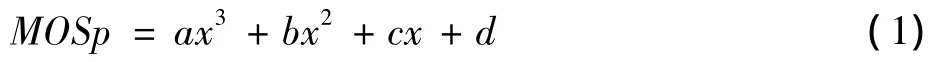
式中:要求式(1)在x定义域范围内保持单调递增。

1.2 评估的三个性能指标

1.2.1 Pearson相关系数(R)

式中:Xi代表主观评分(MOS值);Yi代表客观评分(MOSp值);N代表参与评估的图像总数。Pearson相关系数R衡量了一种算法输出的预测值与主观数据之间的线性关系，值越大，表示算法的单调性越好。

1.2.2 均方根误差(RMSE)

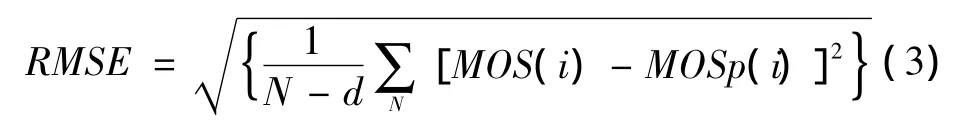
式中:N代表参与评估的图像总数;d表示映射函数方程中自由度的个数，文中d=4。RMSE描述了IQA算法的准确度，值越小，算法的准确度越高。

1.2.3 离散率(Outlier Radio，OR)

式中:1个有效的离散点是满足式(5)约束条件的点。

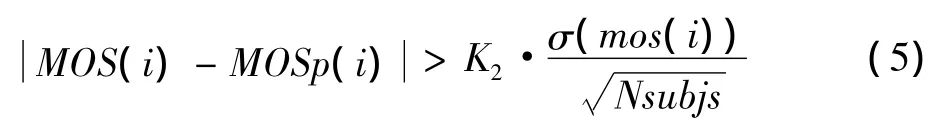
式中:K2=1.96，σ (mos(i))表示与第i幅图像相关的标准差;Nsubjs=33，表示参与评价第i幅图像的人数[8]。OR表征了IQA算法评分与主观评分的一致程度，值越小，算法与主观评分的一致性越好。

2 有约束线性最小二乘法的数学模型

考虑到IQA算法的目的是为了模拟人眼视知觉的判断，本文选定将均方根误差最小化作为回归映射函数的直接目标。将IQA算法应该满足的基本假设为:图像质量越高，即MOS值越大，算法度量值(MOSp)应该越大。因此，在定义域内保持单调递增是回归映射函数需要满足的约束条件。因为均方根运算不影响函数的单调性，所以目标函数的形式可简化为

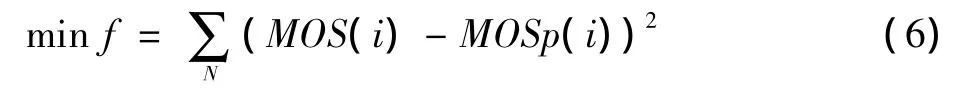
将公式(1)代入式(6)，得

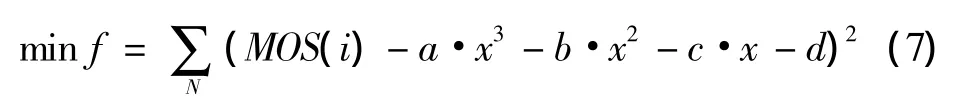
式中:f为因变量，对任何i值，MOS(i)均为常量。以上述形式充当目标函数的方法即为最小二乘法。

当将x作为自变量考虑时，x的定义域可归一化为[0，1]区间，显然公式(1)为连续函数，为了使MOSp(x)在x的定义域内满足单调递增，当且仅当MOSp(x)的一阶导数MOSp'(x)在[0，1]区间满足

式中:目标函数和约束不等式十分复杂。参考文献[12－15]中提及该目标函数和约束条件既不属于多元线性回归问题，也不属于简单的曲线拟合和非线性回归的范畴。从回归分析的角度来看，其可定性为有约束的线性回归问题，此时 a，b，c，d 为待求变量。

当将a，b，c，d看作自变量重新考虑上述过程时，发现公式(8)即为线性约束条件。离散情况下，当x的数据量足够大时，若对每一个x值，均有公式(8)成立，那么可近似认为MOSp(x)在[0，1]区间上单调递增。当然，前者为后者的必要不充分条件，结果是否符合预期需要验证。简言之，对第i幅图像(i=1，2，…，N)，使每一个 MOSp(xi)均满足公式(8)，同时最优化目标函数(7)的值最小，最后通过查看映射函数曲线来反过来验证函数MOSp(x)是否单调。上述即为本文采取的策略，可用数学模型表达为

式中:C 和A 为矩阵;d，b，lb，ub和x为矢量，其中x=[a，b，c，d]为待求变量。

3 实验结果与分析

实验平台采用Matlab实现，其数学模型为

式中:C，A 和 Aeq 为矩阵;d，b，beq，lb，ub 和 x 为矢量，其中x为待求变量。

对本文而言，各参数的含义如下:x=[d，c，b，a]T，，y为某一IQA算法1700 ×1维的度量值其中 mosi表示对应第i幅图像的MOS 值，Aeq=beq=[]，lb=[－Inf，－Inf，－Inf，－ Inf]，ub=[Inf，Inf，Inf，Inf]。上述符号均按Matlab语言表述，由此解得的自变量x即为公式(1)中映射函数的系数。

根据PSNR、SSIM和MSSIM三种算法基于TID2008数据库的计算结果，使用Matlab优化工具箱拟合得到的回归映射函数分别为

式中:psnr_t=psnr/50，使得psnr_t值中99.94%的比例落在区间[0，1]之间。

PSNR、SSIM和MSSIM 3种算法的散点图和回归映射函数曲线如图1所示。图1的横坐标分别表示图像的PSNR、SSIM和MSSIM 算法归一化到[0，1]区间的度量值，这些度量值通过对TID2008图像库的失真图像及其参考图像应用各算法计算得到;纵坐标表示图像的MOS值，数据直接取自TID2008图像库[9]，0值表示主观判断图像质量最差，9表示最好。如果存在理想算法，那么在图1的坐标系下其散点将全部分布在第1象限的某条直线上。观察图1中曲线可知，根据此方法得到的映射函数的确在数据定义域内单调递增。

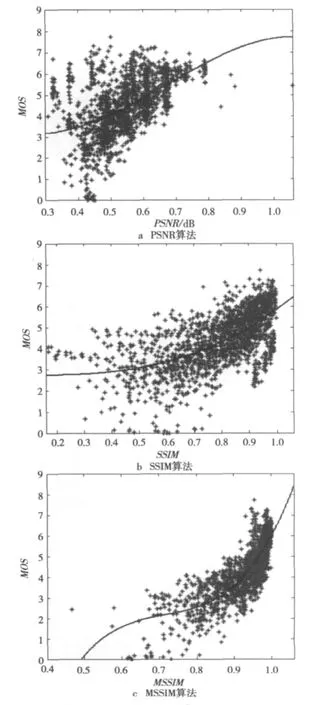
图1 3种算法的散点图和其映射函数曲线

实验所得的统计参量如表1，表2所示。表1为不同算法的统计参量绝对值。该组数据显示，3种算法与MOS值之间的线性相关系数R全部低于90%，RMSE平均相差0.7个等级(全部为0～9共10个等级)，OR系数显示有至少94%以上的算法度量误差阈值大于人眼。表2列出了不同算法的相对差异程度，用0和1表示，0表示两种算法的差异不明显，1表示两种算法间存在显著的差异。由以上两组数据可以得到3种算法的性能排序，但是其结果与人眼判断的MOS值差距很大，均不能令人满意。这组性能指标与文献[6－7]的实验数据相比，数据意义简单、明确，对客观地理解和判断IQA算法的性能有所帮助。

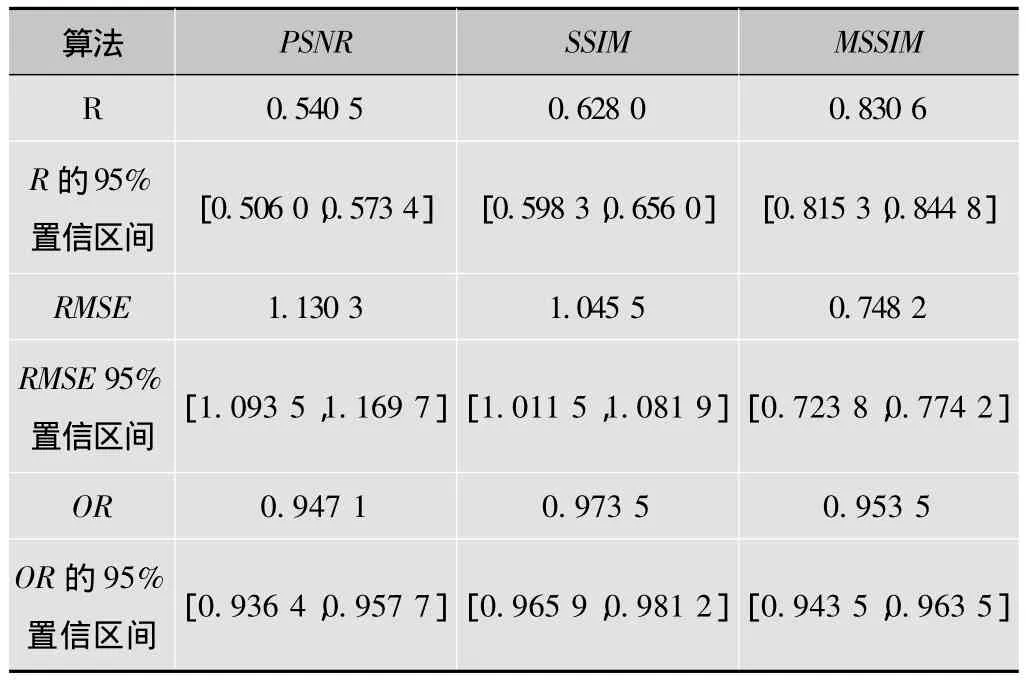
表1 统计参量的绝对值

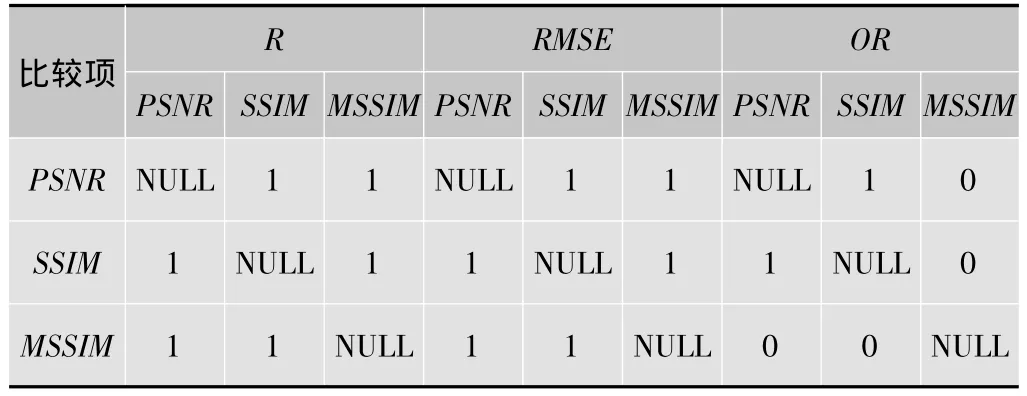
表2 统计参量Pearson CC，RMSE及OR的相对差异显著程度

上述实验结果表明，目前主流的IQA算法与主观评价值之间差异较大，图像的客观评价算法仍有待进一步提高性能。本文提供了一种衡量图像客观评价与主观评价之间差异的方案，为图像评级研究提供了帮助。应该指出，本文的方法还有待完善，如公式(1)不一定满足在[0，1]整个区间内单调递增，具体单调区间受算法的度量值 x的上下限 xmin、xmax影响，只能满足在[xmin，xmax]区间内的单调递增，下一步研究将对该曲线拟合方法继续完善。

4 结论

本文针对VQEG对IQA算法的评估策略，采用基于有约束最小二乘法的数学模型，对算法数据的三次多项式形式非线性回归拟合过程求解。建议的方法约束条件为线性，所以求解过程效率高，可以为研究IQA算法提供性能比较的实验平台。

[1]VQEG.Final report from the video quality experts group on the valida-tion of objective models of multimedia quality assessment，phase I[DB/OL].(2008－09－12)[2011－07－21].http://www.vqeg.org.

[2]VQEG.Final report from the video quality experts group on the validation of objective models of video quality assessment，phase I[DB/OL].(2000－03－03)[2011－07－21].http://www.vqeg.org.

[3]VQEG.Final report from the video quality experts group on the validation of objective models of video quality assessment，phase II[DB/OL].(2003－08－25)[2011－07－21].http://www.vqeg.org.

[4]李永强，沈庆国，朱江，等.数字视频质量评价方法综述[J].电视技术，2006，30(6):74－77.

[5]DOSSELMANN R.An evaluation of existing and emerging digital image and video quality metrics[D].Canada:University of Regina，2006.

[6]WANG Z，BOVIK A C，SHEIKH H R，et al.Image quality assessment:from error visibility to structural similarity[J].IEEE Transactions on Image Processing，2004，13(4):600－612.

[7]SHEIKH H R，SABIR M F，BOVIK A C.A statistical evaluation of recent full reference image quality assessment algorithms[J].IEEE Transactions on Image Processing，2006，15(11):3440－3451.

[8]DOSSELMANN R，YANG X D.A comprehensive assessment of the structural similarity index[J].Signal，Image and Video Processing，2011，5(1):81－91.

[9]PONOMARENKO N，LUKIN V，ZELENSKY A，et al.TID2008 – a database for evaluation of full－reference visual quality assessment metrics[J].Advances of Modern Radioelectronics，2009，10:30－45.

[10]WANG Z，SIMONCELLI E P，BOVIK A C.Multiscale structural similarity for image quality assessment[C]//Proc.the 37th IEEE Asilomar Conference on Signals，Systems and Computers.[S.l.]:IEEE Press，2003:1398－1402.

[11]BOVIK A.The essential guide to image processing[M].Salt Lake City:Academic Press，2009:553－595.

[12]斯皮格尔，希勒，斯里尼瓦桑.概率与统计[M].孙山泽，戴中维，译.2版.北京:科学出版社，2002.

[13]何晓群.实用回归分析[M].北京:高等教育出版社，2008.

[14]DOUGLAS M，DONALD G.非线性回归分析及其应用[M].韦博成，万方焕，朱宏图，译.北京:中国统计出版社，1997:1－71.

[15]MATHEWS J，FINK K.数值方法:MATLAB版[M].周璐，陈渝，钱方，等，译.4版.北京:电子工业出版社，2005:195－213.