带阻容负载的独立发电机整流系统的静态稳定性研究

魏克银 徐俊霞 韩 辉 蒋云昊

（1.中国人民解放军73681部队 南京 210042 2.南京信息工程大学信息控制学院 南京 210044）

1 引言

随着电力电子及其控制技术、各种分布式电源系统的发展，独立发电机二极管整流供电系统的使用已变得越来越普遍[1,2]。然而当参数不合理时，这种系统可能会出现静态稳定性问题（表现为低频振荡，LFO），如文献[3,4]研究的整流电源-逆变器-感应电机负载的舰船电力推进系统的低频振荡问题，文献[5-7]研究的三相/多相发电机整流-反电动势负载系统的低频振荡问题等。在最近的研究中发现，系统参数配合不合理时，同步发电机整流系统带阻容负载时同样会出现静态稳定性问题。图1为带阻容负载的三相发电机整流系统的示意图（隐极发电机转子在交轴方向上布置一套时间常数与励磁绕组时间常数接近的fq绕组[5]），图2为上述系统采用恒压他励方式发生低频振荡时系统励磁电流、相电压、相电流、直流侧电压及整流电流的实验波形图。上述低频振荡给系统在噪声、振动、应力等方面带来了较多的问题，严重影响了系统的安全运行。为了较清楚地了解这种现象发生的机理，并进行有效地抑制，有必要对其进行详细地分析研究。

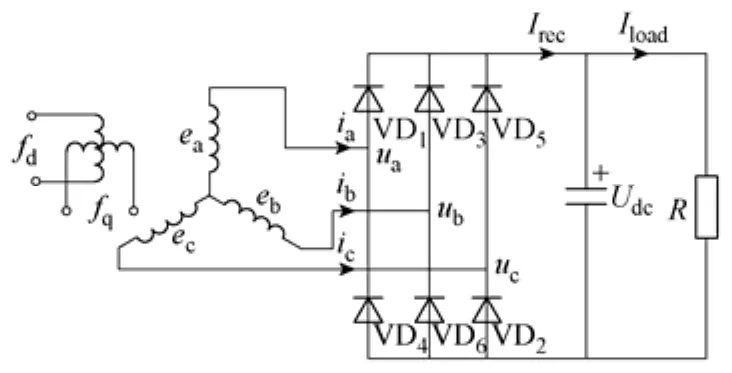
图1 带阻容负载的发电机整流系统示意图Fig.1 Sketch map of generator-rectifier system with capacitor-resistor load

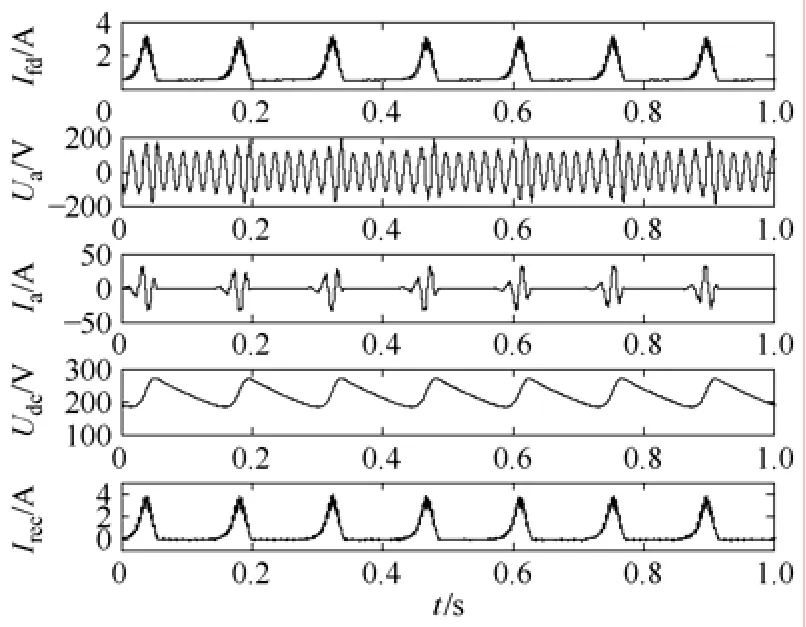
图2 系统发生低频振荡时的实验波形Fig.2 Experimental waveforms of system during a LFO

独立发电机整流系统的静态稳定性问题不外乎有实验、仿真和理论计算等研究方法。实验方法最为客观与直接，可以方便地考虑饱和等多种因素的影响，但部分电机参数（如绕组电阻与电感参数）在实验中不易变化，影响了对系统静态稳定性规律的研究。仿真方法简单易行，只要建立准确的系统仿真模型，特别是电机模型，可以方便地修改任何参数，继而研究它们对系统静态稳定性的影响。但很难做到对电机参数的准确提取及对饱和影响的准确考虑，因而在一定程度上影响了仿真的准确性[8]。研究独立供电系统静态稳定性问题的理论方法可分为时域方法（特征值法）[4-7,9]和频域方法（阻抗/导纳法）[10-12]。时域方法可分为以下几个步骤：①建立电机的降阶模型、二极管整流桥的平均值模型（以将不连续系统转化为连续系统）及负载的动态模型；②在稳态运行点对系统模型进行线性化，得到系统特征方程；③应用Routh-Hurwitz判据进行系统稳定性判断。频域方法也分为以下几个步骤：①、②与时域方法相同；③计算直流电源的输出阻抗和负载的输入阻抗；④应用Nyquist或Middlebrook等判据进行系统稳定性判断。可见，不管是时域方法还是频域方法都需要建立系统在整流桥平均值模型基础上的线性化模型。然而，由于二极管整流桥的状态由流过二极管的电流决定，当直流侧采用不同滤波器时，其动态平均值模型的推导有很大的差别。当整流桥直流侧采用L滤波或LC滤波时，其直流侧电流较为平直，状态空间平均值模型较容易建立[13,14]，但当直流侧仅有电容滤波器时，直流侧电压较平滑，而直流侧电流的脉动较大，其平均值模型的求解需要应用数值叠代的方法[15]，而更为复杂的系统线性化模型的得到则需要借助ACSL或Matlab/Simulink等软件工具[16]。频域方法有时还存在给出的稳定性条件过于苛刻的问题，即当电源输出阻抗和负载输入导纳关系不满足稳定性判据时，实际系统仍可能是稳定的，对稳定域的精确判断十分困难[12]。

文献[5-7]解释了带反电动势负载的发电机整流系统静态稳定性问题的物理机理，认为是交轴电抗与直轴瞬态电抗之比过大（表现为临界稳态电阻大于折算到交流侧的等效直流动态电阻）导致了系统的静态不稳定性，并认为直流侧电流微分负反馈或在转子上设置时间常数与励磁绕组接近的交轴短路绕组可以有效抑制系统低频振荡的发生。文献[3]认为是恒功率负载的负阻抗特性引起了其系统的不稳定，本文中的负载显然不属于这一类情况。由于直流侧电容的存在，本文系统无法得出等效直流动态电阻的概念，因而无法像文献[5-7]一样应用Roth-Hurwitz判据进行系统稳定性判断。

发电机整流带阻容负载的系统结构虽不新颖，但目前尚没有文献系统研究其静态稳定性问题。本文根据此类系统在临界稳定时的运行特点，分别运用理论分析、实验与仿真等方法较为全面、系统地研究了其静态稳定性问题，其中稳定性的理论计算运用了系统特征值理论。总结了系统静态稳定性问题的一般规律，分析了其物理机理，并研究了抑制此类系统静态不稳定的措施。

2 理论分析

2.1 三相同步发电机的简化模型与稳态值计算

稳态或似稳态时，可将发电机定、转子电流与磁链分解为高频与低频分量分别处理。若忽略发电机定子绕组暂态，转速维持在额定值，在理想化电机假设的条件下，可得到发电机如图3所示的等效电路模型及xad标么值系统下如式（1）所示的端电压方程[5]

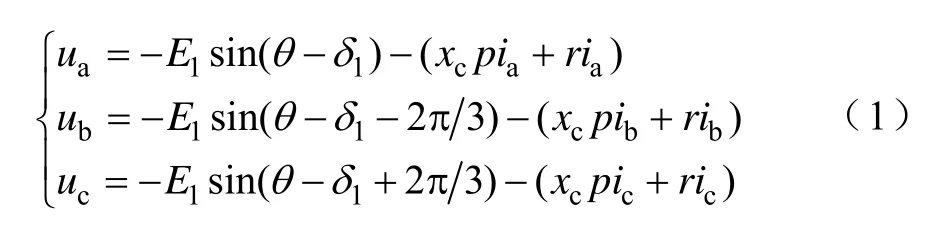
式中，E1为图3中等效理想电压源幅值；δ1为基波功率角；xc=(x″d+x″q)/2，为等效换相电抗；p为微分算子；r为相电阻。且有

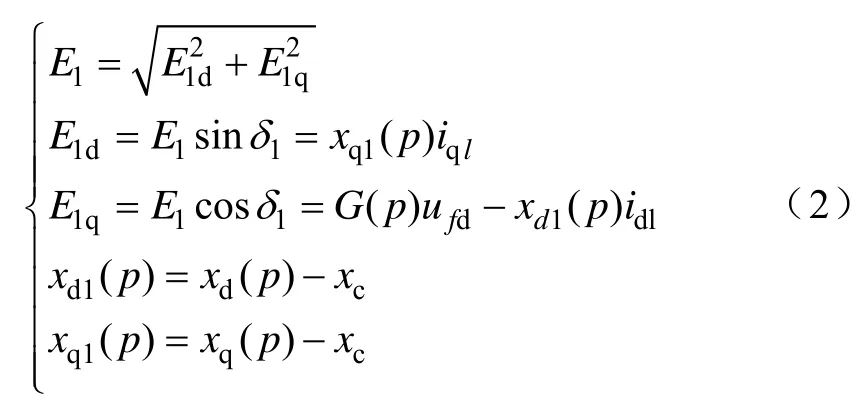
式中，G(p) 为运算电导；idl、iql分别为定子直轴电流与交轴电流的低频分量；xd(p)、xq(p) 分别为直轴、交轴运算电抗。

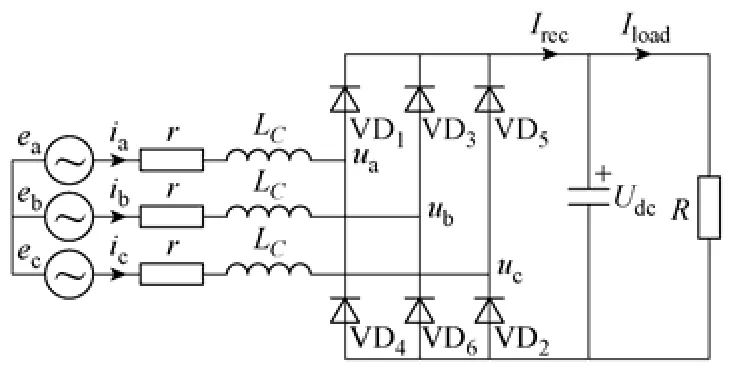
图3 三相同步发电机的等效电路模型Fig.3 Equivalent circuit model of 3-phase synchronous generator

定义纵轴瞬变电动势E′q=xadψfd/xfd、横轴瞬变电动势E′d=-xaqψfq/xfq，则可以建立发电机以E′q、E′d为状态变量的二阶简化模型。

式中，Td0=xfd/rfd、Tq0=xfq/rfq分别为转子励磁绕组和交轴绕组的时间常数，x′q1=x′q-xc、x′d1=x′d-xc，且有

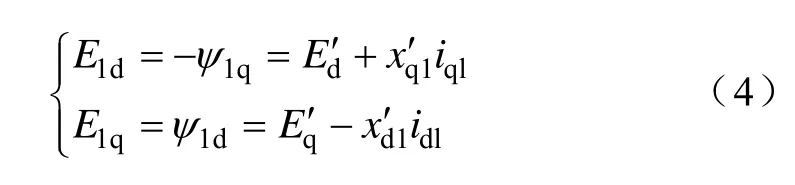
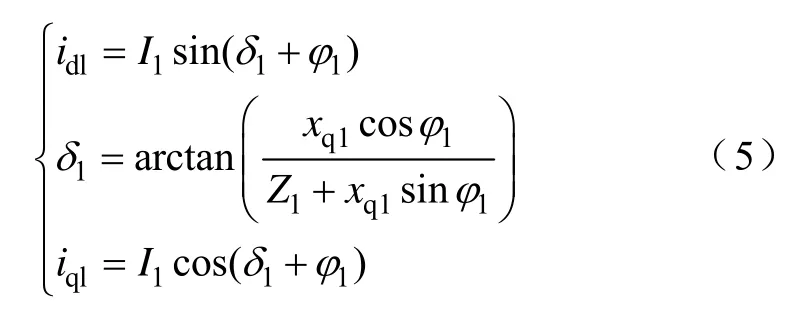
2.2 整流桥的平均值模型及负载方程

从仿真与实验研究中发现，系统从轻载到重载区间内都可能发生低频振荡现象，但系统在两种极端情况下临界稳定时，整流桥都工作于连续导通模式，图4所示为重载临界稳态时发电机内电动势与相电流波形。可见，由于交流侧电感的作用，直流侧电流仍较平滑。因此，依据文献[17]中的状态空间平均值法，可建立图3中整流桥的动态平均值模型

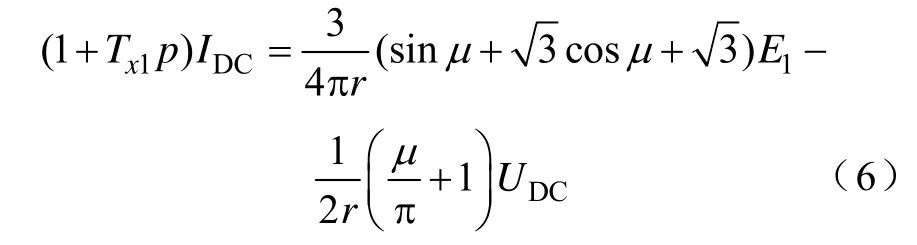
式中，Tx1=LC/r，IDC、UDC分别为直流侧电流与电压平均值；μ为换相重叠角。

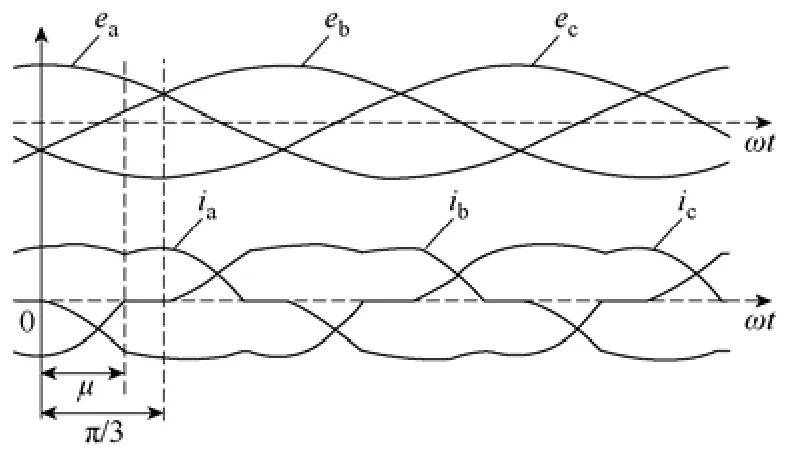
图4 等效理想电压源与相电流波形Fig.4 Waveforms of equivalent ideal voltage source and phase current of generator

由文献[5,6]易知

直流侧负载方程可表示为

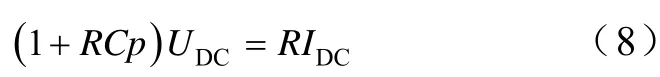
2.3 系统的线性化模型

式（3）、式（6）与式（8）构成了系统的状态空间模型，由于IDC作为系统状态变量时不如I1方便，因此，应用式（7）中第3行等式对式（6）、式（8）中的IDC作相应的代换，得到系统新的状态空间模型

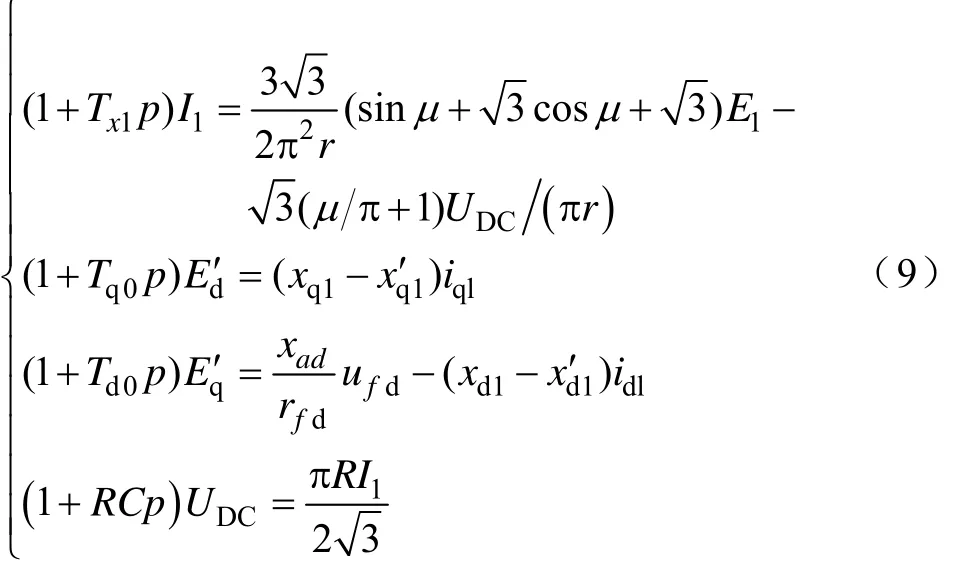
对系统方程式（9）作一阶线性化处理，并通过式（2）、式（4）、式（5）与式（7）将系统方程变换为以Ed′、Eq′、I1、UDC为状态变量的小信号模型。

式中，c1～c9为变量系数，由系统参数确定。

2.4 系统运行稳定性分析

为简化分析，认为发电机转子上不设置fq绕组，则Tq0=0、xq′=xq、xq′1=xq1、Ed′Δ=0，系统的特征方程为

上述系统稳定时，其特征根将具有负的实部，且系统稳定性越好，其负实部的绝对值越大。考察每个特征根的阻尼强度，也可判断系统的相对稳定性。

3 系统静态稳定性的规律及实验、仿真与理论的相互验证

为总结系统静态稳定性的规律，作者在一套带阻容负载的三相同步发电机整流系统（PN=20kW，UN=380V，cosφ=0.8，电磁参数如表1所示）上进行了大量的实验、仿真与理论计算，总结出以下几条规律：①发电机励磁绕组与电枢绕组的漏感参数越大，系统的稳定性越好；②发电机交轴阻尼作用越强，系统的稳定性越好；③随着发电机饱和度的提高，系统的稳定性变好；④直流侧电容越小，系统的稳定性越好；⑤只有当电阻属于某一区间时（即负载功率不太大也不太小），系统才可能发生低频振荡，且在此区间内存在一电阻可使系统的低频振荡最为严重。

表1 发电机的电磁参数（标幺值）Tab.1 The electromagnetic parameters of generator（pu）

当C=3.5mF、R=30Ω时，给发电机施加31V的阶跃励磁电压，系统将发生低频振荡。图5所示为在EMTDC软件环境中，测试不同阻尼绕组电阻对系统静态稳定性影响的结果，其中图5a中阻值为电机电磁参数设计计算值。可见，直轴阻尼对系统静态稳定性影响不大，而交轴阻尼作用增强后，系统的静态稳定性得到明显改善。

图5 阻尼绕组对低频振荡的影响Fig.5 The effect on LFO from damper windings

图6 所示为综合考虑电容与电阻对系统静态稳定性影响的实验与仿真结果。仿真给出了电容与电阻变化时系统临界稳定的边界，可见，只有当电容大于某一值时，系统才可能出现静态不稳定，而在负载太大或太小时，系统都将稳定。图中作标志的点为实验结果（△表示稳定运行点，□表示临界稳定点，○表示不稳定点）。可见，仿真与实验结果基本一致。

图6 电容与电阻对系统静态稳定性的综合影响Fig.6 The associated effect of capacitor and resistance on system LFO

从图6仿真结果中可知，当系统在电容为3.5 mF、4.5mF达到临界稳定时，较小的临界电阻分别为18.0Ω与16.1Ω。根据上文中准稳定系统特征值的计算方法，表2、表3分别列出了在电容为3.5mF与4.5mF，并带不同负载电阻时系统特征值的理论计算结果。从表2与表3中可见，在电容为3.5mF、4.5mF时，当负载电阻约为15.0Ω 及13.0Ω 时系统达到临界稳定，且随着负载电阻减小（负载功率增大），系统的稳定性变好，这与图6显示基本一致。当系统负载较轻时，直流侧电流脉动较大，此时整流桥平均值模型的效用变差，基于此计算出的系统特征值不能准确验证系统静态稳定性。

表2 C=3.5mF时的系统特征值Tab.2 System eigenvalue when C=3.5mF

表3 C=4.5mF时的系统特征值Tab.3 System eigenvalue when C=4.5 mF

4 系统低频振荡的机理

将式（7）第2行代入式（6）得

式（14）揭示了系统“微变”稳定性条件的机理：当小扰动引起电枢电流增大时（即ΔI1＞0），励磁电流Ifd增大以维持磁链ψfd不变，发电机的等效电动势将增大（ΔE1＞0），同时，直流侧负载压降也将增大（ΔUDC＞0）。如果发电机等效电动势增量小于直流侧负载压降增量（折算到交流侧，k2可认为是整流桥两侧电压折算系数或变比），则电枢电流将减小，使系统恢复到原来的平衡状态，即系统在该平衡状态下能够稳定运行；反之，若发电机等效电动势增量大于直流侧负载压降（折算到交流侧），则电枢电流将进一步增大，使系统逐渐远离原来的平衡点，即系统在该平衡状态下不能够稳定运行。对于小扰动引起电枢电流减小时系统的稳定性可类似上文分析。

5 系统低频振荡的抑制方法

5.1 从参数角度的抑制方法

系统参数影响低频振荡的发生及强弱，从参数的角度可采取以下措施抑制系统的静态不稳定：①增大发电机励磁绕组与电枢绕组的漏感；②增大发电机交轴阻尼绕组的电感，减小其电阻；③减小负载电容；④选择适当阻值的电阻负载；⑤选择恒流源作为发电机的励磁电源。图7a与图7b所示为C=3.5mF、R=30Ω，发电机励磁电源分别为74V的恒压源与2A的恒流源的直流侧电压仿真波形。可见，恒流源给发电机磁场供电时，系统不会发生静态不稳定现象。这是因为励磁电流为恒流时，若系统出现扰动，则励磁绕组的磁链不再守恒，因而这个扰动不会引起ΔI1发散，因而系统能够维持稳定。当然，也不能为了避免系统不稳定，而任意改变上述参数，如绕组漏感的增加将加大电机的时间常数，阻尼绕组电阻、电感的大小受电机结构及工况的限制，而负载电容与电阻有时不能任意改变。

图7 直流侧电压波形Fig.7 Waveforms of DC bus voltage

5.2 从控制器角度的抑制方法

从控制的角度也可以减轻或避免系统的运行不稳定。如图8所示，当系统以直流侧电压为整定对象时，给定直流侧电压参考值，取直流侧电压为负反馈量。为抑制系统静态不稳定，在控制器的输入端可加入直流侧电压微分负反馈。图中G1为励磁功率放大器，发电机以一阶惯性节表示，将发电机等效内电动势与直流侧电压表示成线性关系[6]。图7c中所示为C=3.5mF、R=30Ω，Udc-ref=479V时，系统采用直流侧电压负反馈加微分负反馈控制方式时的直流侧电压波形。可见，上述控制方式有效抑制了系统的运行不稳定，但控制器的引入增大了系统的时间常数。

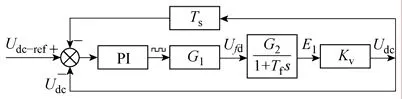
图8 低频振荡的控制措施Fig.8 The control method for LFO

6 结论

本文较为详细地研究了带阻容性负载的独立三相发电机整流系统的静态稳定性问题。建立了包括二阶发电机模型、二极管整流桥的动态平均值模型及负载动态模型在内的系统状态空间模型及运用线性化方法建立的小信号模型，运用系统特征值理论判断了带阻容性负载的独立三相发电机整流系统的静态稳定性。结合实验与仿真分析方法，总结了上述系统运行稳定性的规律，并分析了其不稳定的物理机理。论文还从参数与控制策略的角度提出了增强系统运行稳定性的措施。

[1] IEEE Committee Report.IEEE standard definitions for excitation systems for synchronous machines[S].IEEE Std 421.1™—2007,July 2007.

[2] Warner T H Kassakian J G.Transient characteristics of large turboalternator driven rectifier/inverter system based on field test data[J].IEEE Transactions on Power Apparatus Systems,1985,104(7): 1804-1811.

[3] Sudhoff S D,Coorzine K A,Glover S F,et al.DC link stabilized field oriented control of electric propulsion systems[J].IEEE Transactions Energy Conversion,1998,13(1): 27-33.

[4] 郭云珺,王东,刘德志,等.变频驱动三相感应电机系统稳定性的数学推导与分析[J].电工技术学报,2010,25(9): 47-55.Guo Yunjun,Wang Dong,Liu Dezhi,et al.Mathematical deduction and stability analysis of three-phase inverter-fed induction motor drive system[J].Transactions of China Electrotechnical Society,2010,25(9): 47-55.

[5] 马伟明.十二相同步发电机及其整流系统的研究[D].北京: 清华大学,1995.

[6] 张晓锋.同步发电机整流系统的运行稳定性研究[D].北京: 清华大学,1995.

[7] 杨青.交直流混合独立供电系统运行稳定性研究[D].武汉: 海军工程大学,2003.

[8] Wu Xusheng,Ma Weiming,Sun Junzhong,et al.Parameter measurement of multi-phase synchronous machines with AC and DC output[C].Proceedings of the 5th International Conference on Electrical Machines and Systems,Shenyang,2001: 587-591.

[9] Ma Weiming,Hu An,Liu Dezhi,et al.Stability of a synchronous generator with diode-bridge rectifier and back-EMF load[J].IEEE Transactions Energy Convetsion,2000,15(4): 458-463.

[10] 陈明亮.电力电子变换器端口特性分析及应用研究[D].武汉: 海军工程大学,2007.

[11] Belkhayat M.Stability criteria for AC power systems with regulated loads[D].Indiana: Purdue University,1997.

[12] Sudhoff S D,Glover S F,Lamm P T,et al.Admittance space stability analysis of power electronic systems[J].IEEE Transactions Aerospace Electronics System,2000,36(3): 965-973.

[13] Sudhoff S D,Corzine K A,Hegner H J,et al.Transient and dynamic average-value modeling of synchronous machine fed load-commutated converters[J].IEEE Transactions on Energy Conversion,1996,11(3): 508-514.

[14] Huiyu Z,Burgos R P,Lacaux F,et al.Evaluation of average models for nine-phase diode rectifiers with improved AC and DC dynamics[C].Proceedings of the 21st IEEE Annual Conference on Applied Power Electronics Conference and Exposition,Dallas,TX,USA,2006: 1324-1330.

[15] Alt J T,Sudhoff S D,Ladd B E,Analysis and average-value modeling of an inductorless synchronous machine load commutated converter system[J].IEEE Transactions Energy Conversion,1999,14(1): 37-43.

[16] Simulink—Writing S-Functions,6th ed.[Z].The Math Works,Inc.,Natick,MA,2002: 2-9–2-12.

[17] Sanders S R,Verghese G C.Synthesis of averaged circuit models for switched power converters[J].IEEE Transactions on Circuits and Systems,1991,38(8):905-915.