考虑压力变化的超磁致伸缩超声换能器动态模型

曾建斌 白保东 曾庚鑫 曾海泉 李永建

（1.沈阳工业大学电气工程学院 沈阳 110870 2.华南理工大学机械与汽车工程学院 广州 5106402 3.厦门理工学院机械系 厦门 361024 4.河北工业大学电气工程学院 天津 300130）

1 引言

由美国海军水面武器中心发明的被称为Terfenol-D的稀土超磁致伸缩材料，具有磁致伸缩应变大、能量密度高、响应速度快、输出功率大、转换效率高以及居里点温度高等特点，已经在精密加工、水声工程和微型机电系统等领域得到了广泛地应用。由于其相对高的导热能力，使得超磁致伸缩材料在功率超声领域的优势尤为突出[1]。

热量的产生和散发是制约超磁致伸缩功率超声换能器功率提升的关键问题。换能器的热量主要来自磁滞损耗、涡流损耗、线路电阻损耗及机械阻尼损耗，磁滞损耗是最主要的也是最难解决的问题。

目前针对超磁致伸缩材料及器件磁滞现象的研究多数集中于磁滞对于运动轨迹的影响，且一般针对低频执行器（作动器），有关超磁致伸缩材料磁滞损耗大小的文献很少，未见用Jiles-Atherton 磁滞数学模型[2,3]计算超磁致伸缩换能器磁滞损耗的报道，针对国产超磁致伸缩材料这方面的研究更是空白。因此，对这方面的研究是很有必要的，只有将磁滞生热机理及其影响因素研究清楚，才能在设计中对导致生热的因素加以抑制，减少热量的产生和能量的消耗，并采取相应的散热措施。

本文以台州椒光稀土材料有限公司生产的Terfenol-D超磁致伸缩材料为致动元件，设计一台超声换能器原型，并对其进行了实验测试，得到了第一手的实验数据，并在此基础上提出了考虑压力变化的反向Jiles-Atherton磁滞模型。

2 超磁致伸缩超声换能器的机械结构

本文设计的Terfenol-D超磁致伸缩超声换能器的结构如图1所示。在位于上导磁环和下导磁环之间的线圈中通入固定频率的交变电流，会在换能器内部激发一个交变的磁场，交变磁场使内部超磁致伸缩棒产生振动，振动通过下导磁片等零件传到外部。

3 原始Jiles-Atherton磁滞数学模型

目前对超磁致伸缩材料磁滞特性的研究大多建立Jiles-Atherton磁滞数学模型的基础上，因此下面将对该磁滞数学模型作一个简要的介绍。

在原始的Jiles-Atherton磁滞数学模型中，磁性材料的磁化强度由可逆磁化分量Mrev和不可逆磁化分量Mirr构成，如下式所示：

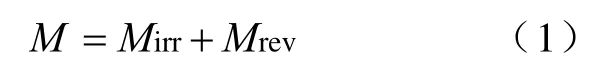
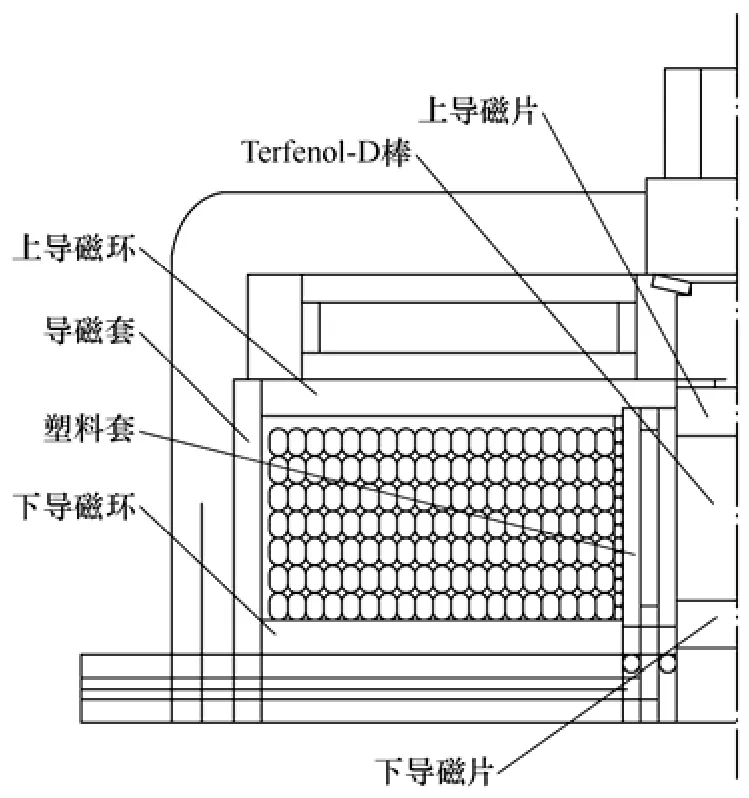
图1 Terfenol-D超磁致伸缩超声换能器的结构Fig.1 Structure of Terfenol-D magnetostrictive ultrasonic transducer

考虑的磁性材料的实际磁化过程，可逆磁化分量和不可逆磁化分量与非磁滞磁化强度Man的关系可以由下式给出：

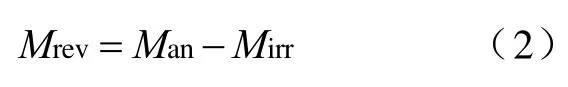
非磁滞磁化强度Man可以由下面的朗之万函数和外斯分子场理论来来描述，如下所示：

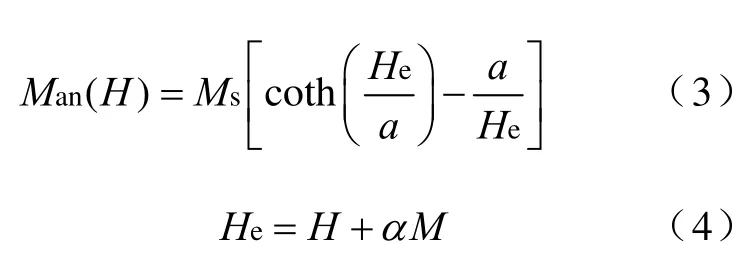
式中，He和Ms分别为有效场强度和材料的饱和磁化强度；α是平均场参数代表着畴壁之间的耦合强度，可以通过实验测试的方式得到；Ms可以通过磁性材料的数据手册查得。

因为在磁化的过程中，发生了一部分能量的损耗，因此引入参数c（0＜c＜1），来代表这部分能量的损失。这样磁化强度M可以用下式表述：

将式（2）代入式（5）得到

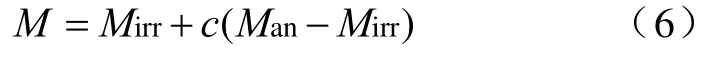
最后Jiles-Atherton磁滞数学模型可以用下面的微分方程来描述：

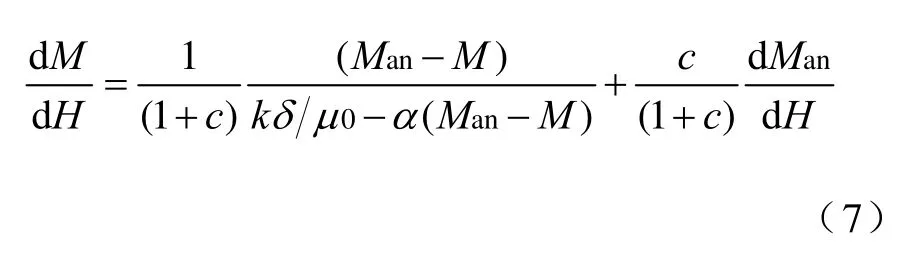
4 考虑应力的反向Jiles-Atherton磁滞数学模型

原始的Jiles-Atherton磁滞数学模型给出了磁化强度M和磁场强度H之间的关系。通常在磁场有限元分析的过程中可以采用面电流法和体电流法，引入原始的Jiles-Atherton磁滞数学模型，来模拟磁化过程。但是这两种方法不但编程实现起来比较烦琐，而且磁场求解过程不容易收敛。

由于在以磁矢量位为未知数的磁场有限元分析中，磁通密度B是比磁化强度M更容易求得，如果能通过B求得H，将大大降低编程实现的难度并加快磁场求解过程收敛速度。反向Jiles-Atherton磁滞数学模型[4]正好能满足上述的要求。

下面对在时步法有限元分析过程中，已知B通过反向Jiles-Atherton磁滞数学模型求得H的过程逐步进行介绍。

首先假设B(t)和H(t)在时步t的磁场计算中得到，而且B(t+Δt)通过磁场分析得到，它们都为已知量，则H(t+Δt)的计算步骤如下：

利用式（8），计算得到时步t和（t+Δt）之间B的差值

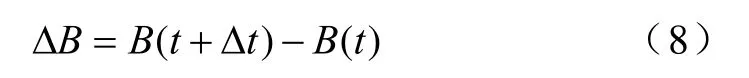
利用式（9），通过时步t的B(t)和H(t)可以计算得到M(t)

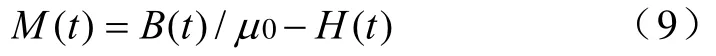
有效磁场强度He(t)可以通过式（10）和式（11）计算得到。

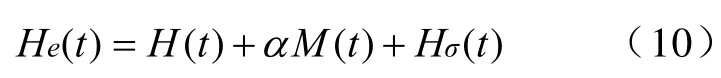
式中，α是平均场参数代表着畴壁之间的耦合强度；Hσ(t)是恒定压力对有效场的影响[5,6]。它由下式来近似确定。

式中，λ和σ分别为磁致伸缩材料产生的应变及它所受到的应力。磁致伸缩材料的应变λ和磁化强度M之间的关系[7-9]为

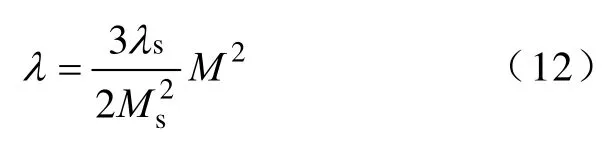
式中，λs为饱和磁致伸缩；M为材料的磁化强度；Ms为材料的饱和磁化强度。将式（12）代入式（11）得到

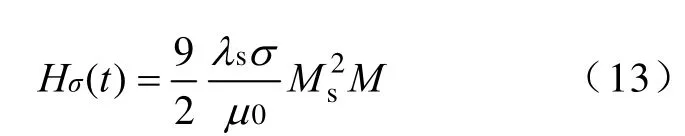
于是式（10）可以重新写成为

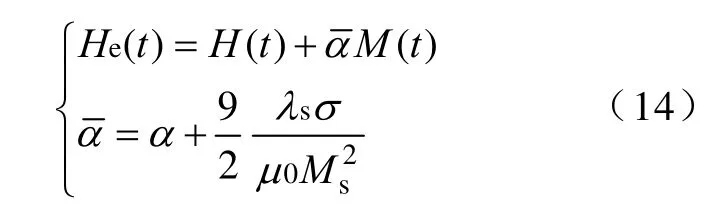
原来的参数α就被新的参数所代替，同时应力的作用在这个模型里被考虑了进来。

通过式（14）和朗之万函数可以计算得到时步t的非磁滞磁化强度Man(t)

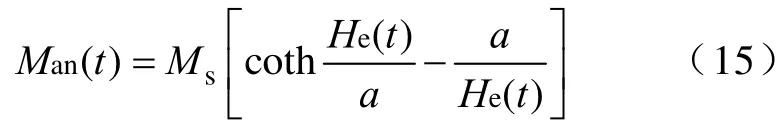
磁化强度M(t)的不可逆分量Mirr(t)可以通过式（16）得到，这里c(0＜c＜1＝是代表磁化过程部分能量的损失的参数。

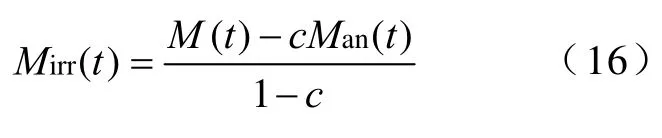
通过式（17）和式（18）可以分别计算得到Man对He的导数和Mirr对Be的导数

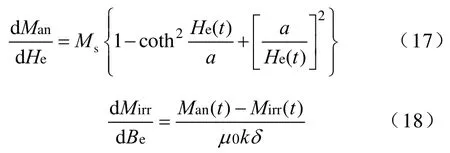
通过下式可以得到磁化强度M对B的导数

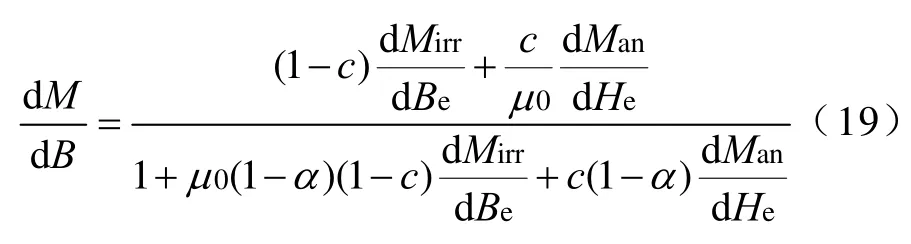
最后（t+Δt）时步的磁化强度M(t+Δt)和磁场强度H(t+Δt)通过式（20）和式（21）计算得到。

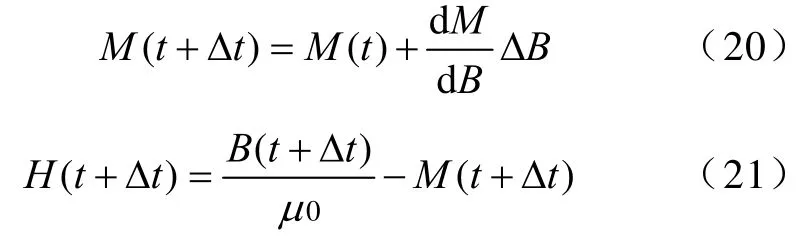
上述为考虑了应力影响的反向Jiles-Atherton磁滞数学模型，将该模型与电磁场有限元分析程序相结合，使得在对超磁致伸缩超声换能器内部的磁场进行有限元计算的过程中不但考虑了磁滞损耗问题，同时还考虑的磁致伸缩材料所受的应力对磁场的影响。磁滞损耗可以在磁场计算完成后，对超磁致伸缩材料每个单元B和H之间的数值积分结果进行累计得到[10]。

5 模型实验与验证

本文对自行设计的超磁致伸缩超声换能器模型进行了不同工作情况下超磁致伸缩换能器的磁滞回线和超磁致伸缩材料的温升进行了测试。图2和图3为实验的接线原理图和实验现场。

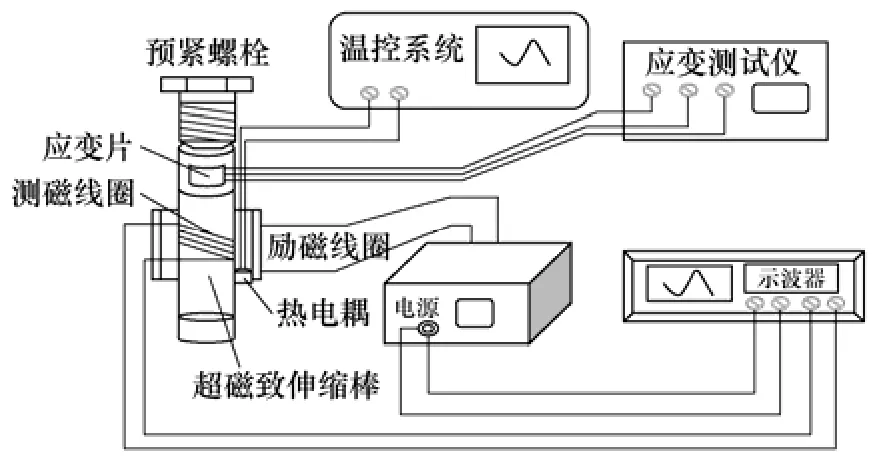
图2 实验接线的原理图Fig.2 Schematic of test system

图3 实验现场Fig.3 Experimental site

取电流频率为20kHz，预紧应力为6.1MPa的H-B曲线数据进行模型的参数提取，提取得到的参数如下表所示，这些参数代入模型计算得到的磁滞回线与实测曲线对比如图4所示。

表 电流频率20kHz预紧应力6.1MPa的模型参数Tab.Model parameters on current frequency 20kHz and 6.1MPa

将上面的参数代入时步法磁场有限元分析程序里，进行换能器的磁场分析。在磁场分析计算的过程中，将电流变化的一个周期离散为180个时步，对于每一时步，进行磁场分析，计算Terfenol-D材料中每个单元的磁场强度H和磁通密度B。图5为第45个时步，换能器内部的磁场分布。

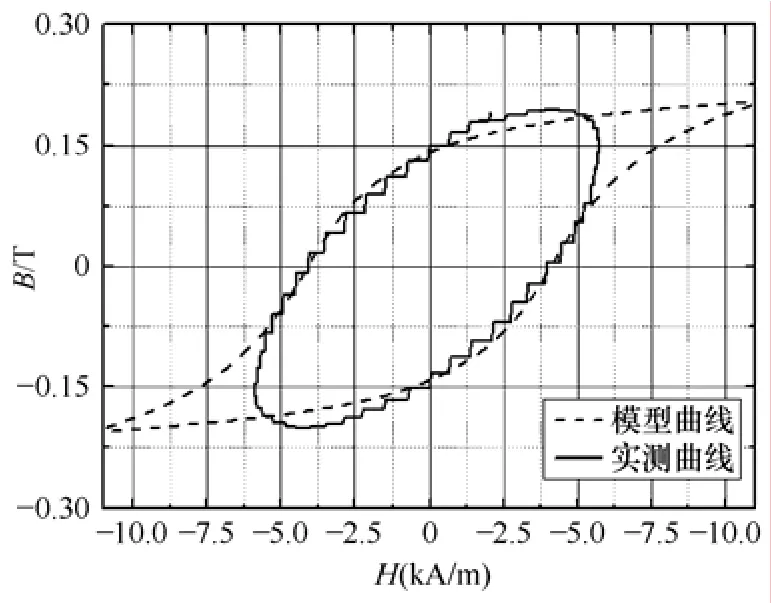
图4 频率20kHz模型曲线和实测曲线对比图Fig.4 Model curve and experimental curve on 20kHz

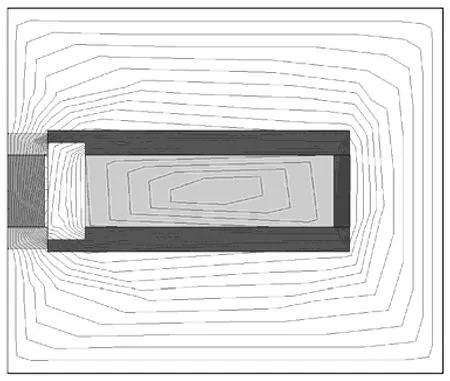
图5 第45个时步Terfenol-D换能器的内部磁场分布Fig.5 Magnetic field distribution of Terfenol-D magnetostrictive ultrasonic transducer in No.45 time-step

完成所有时步的计算后，对超磁致伸缩材料内部单元作H对B的数值积分，得到每个单元的磁滞损耗，通过累加从而得到总的磁滞损耗。最后计算得到磁滞损耗的理论值为72.18W。

最后，计算得到的磁滞损耗作为主要热源导入到有限元软件中，进行换能器的温度场分析，得到换能器内部的温度场分布图，如图6所示。由图可见，超磁致伸缩材料周围的温度为32.0℃，而实际测量值为34.25℃。

误差分析：从上述计算可以看出，超磁致伸缩材料周围的温度计算值与实测值的相对误差为-6.52%。本文认为，引起误差的原因为模型计算得到的磁滞回线与实际测得的磁滞回线不能完全重合，而引起该现象的原因为超磁致伸缩超声换能器的工作频率比较高，而Jiles-Atherton磁滞模型没有考虑磁场变化的频率，因此引入了磁滞损耗计算的误差，最后导致了温升计算的误差。

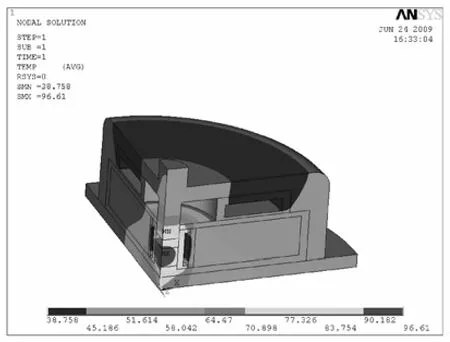
图6 四分之一结构的热分布图Fig.6 Thermal distribution of a quarter of Terfenol-D ultrasonic magnetostrictive transducer.

6 结论

本文提出一种基于反向Jiles-Atherton磁滞数学模型的，考虑应力影响的磁滞数学模型，并将它与时步法电磁场有限元分析法结合，进行超磁致伸缩超声换能器磁滞损耗的计算，然后将计算得到的结果作为热源进行超声换能器的温度场分析，得到超声换能器内部的温度场分布，为换能器强制冷却系统的设计提供了理论依据。在今后的研究工作中，将在磁滞损耗的计算过程中考虑磁场交变的频率对Terfenol-D材料磁化过程的影响，使磁滞损耗的计算更加准确。

[1] Nick Weisensel G,Toby Hansen T,William D Hrbek.High power ultrasonic Terfenol-D transducers enable commercial applications[C].Proceedings of The International Society for Optical Engineering,1998,3326: 450-458.

[2 Jiles D C,Atherton D L.Theory of ferromagnetic hysteresis[J].Journal of Magnetism and Magnetic Materials,1986,61(2): 48-60.

[3 Jiles D C,Thoelke J B.Theory of ferromagnetic hysteresis: determination of model parameters from experimental hysteresis loops[J].IEEE Transaction on Magnetics,1989,25(5): 3928-3930.

[4] Sadowski N,Batistela N J,Bastos J P A,et al.An inverse jiles-atherton model to take into account hysteresis in time-stepping finite-element calculations[J].IEEE Transactions on Magnetics,2002,38(2):797-800.

[5] Calkins F T,Smith R C,Flatau A B,et al.Energy-based hysteresis model for magnetostrictive transducers[J].IEEE Transactions on Magnetics,2000,36(2): 429-439.

[6] Jiles D C.Theory of the magneto-mechanical effect[J].Journal of Physics D: Applied Physics,1995,28(8):1537-1546.

[7] Julie C Slaughter,Marcelo J Dapino,Alison B Flatau,et al.Modeling of a Terfenol-D ultrasonic transducer[C].Proceedings of the International Society for Optical Engineering,2000,3985:366-377.

[8] Fredrik Stillesjo ,Goran Engdahl,Zhongguo Wei,et al.Dynamic simulation and performance study of magnetostrictive transducers for ultrasonic applications[C].Proceedings of The International Society for Optical Engineering,2000,3992:594-602.

[9] 贾振元,王福吉,张菊,等.超磁致伸缩执行器磁滞非线性建模与控制[J].机械工程学报,2005,41(7): 131-135.Jia Zhenyuan,Wang Fuji,Zhang Ju,et al.Hysteresis nonlinearity modeling and control of giant magnetostrictive actuator[J].Chinese Journal of Mechanical Engineering,2005,41(7): 131-135.

[10] Righi L A,Sadowski N,Carlson R,et al.A new approach for iron losses calculation in voltage fed time stepping finite elements[J].IEEE Transactions on Magnetics,2011,37(5): 3353-3356.