适合近岸管节水下施工的测量塔全站仪定位方法
2012-06-06吴瑞大方长远
吴瑞大,方长远
(1.中交第四航务工程局有限公司,广东 广州 510231;2.中交四航局第二工程有限公司,广东 广州 510300)
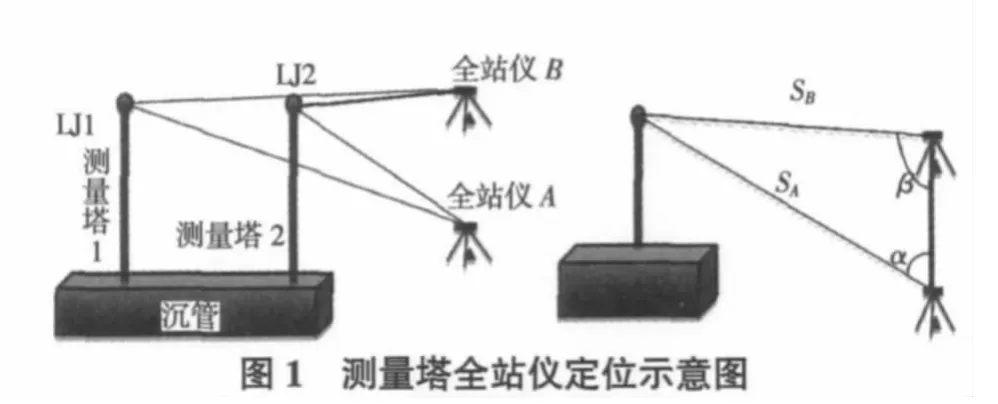
沉管隧道施工时对管节的沉放和对接定位精度要求非常高,在近岸管节水下施工中,常采用测量塔全站仪定位方式[1-2]。施工中将棱镜安装于已固定在待沉管节上方的测量塔上,2台全站仪分别安置于附近岸边的已知点上(如图1所示)。管节沉放和对接过程中,全站仪实时跟踪棱镜,测量斜距S、垂直角δ、水平角α/β和初始方位角A0,并根据这些测量元素,计算不同时刻棱镜的三维坐标,进而确定待沉管节相对于已沉管节的位置。
根据几何定位原理,基于全站仪测量定位有多种观测方式,如交会法和极坐标法,在交会法中又有边交会、角交会和边角交会[1-3]。这些方法观测元素各不相同,其中边交会法观测元素为全站仪到棱镜距离SA和SB;角交会法为水平角度α和β;边角交会则需要观测所有的边元素和角元素。极坐标法则需要观测一条边和该边对应的角度。所有的观测方法均需要观测天顶距h1和h2。可以看出,观测方法不同,观测元素不同,那么这些观测方法的精度如何?能否在精度和作业方式上满足管节施工要求,尤其是动态作业要求?这些均是工程作业人员非常关心的问题,而目前相关研究较少[4]。为此,本文在系统研究各自定位原理、误差和作业方式的基础上,提出满足近岸管节水下施工定位精度的最优测量塔全站仪定位法,可为实际工程应用服务。
1 测量定位方法理论计算模型及其误差模型推导
根据计算方式的不同,棱镜实时三维位置的确定可通过两种方式获得,即前方交会法和极坐标法。以下推导这两种方法的位置计算模型。
1.1 前方交会法
借助实测的全站仪到棱镜距离SA和SB,以及角度α和β,结合两已知点坐标,计算棱镜的三维坐标,有角交会、边交会和边角交会3种方法,以下推导各自的定位和误差模型。
1) 基于角(α、β) 交会的棱镜定位模型及误差模型推导。
若基于已知点A全站仪观测数据确定P点坐标,则有:
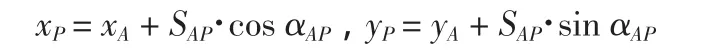
如图1,A、B、P(LJ1/LJ2)按逆时针编号时,将αAP=αAB-α带入上式,得:
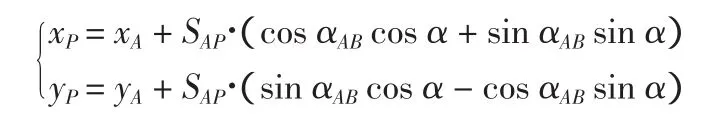
顾及 xB-xA=SAB·cosαAB,yB-yA=SAB·sin αAB,根据正弦定理则有:
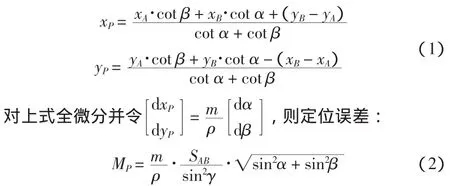
2)基于边(SA、SB)交会的棱镜定位模型及误差模型推导。
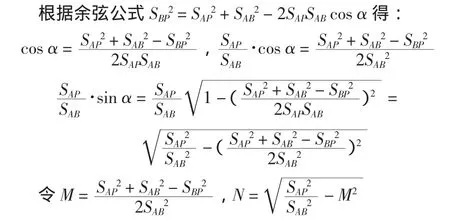
则P点的坐标为:
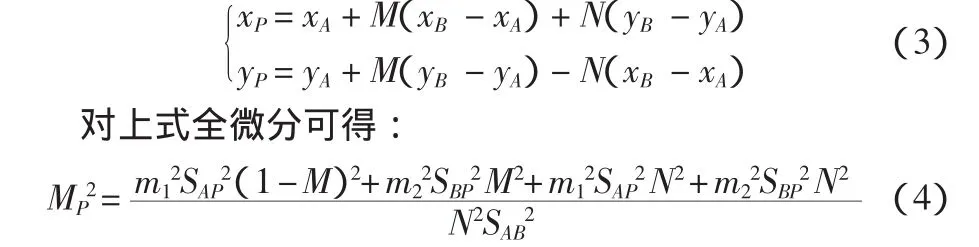
3) 基于边角网 (SA、SB、α和 β) 的棱镜定位模型及其误差模型推导。
将各观测量视为独立观测情况,观测数n=4,必要观测值t=2,多余观测r=2,则采用间接平差,u=2,方程数c=4,构建如下方程组:
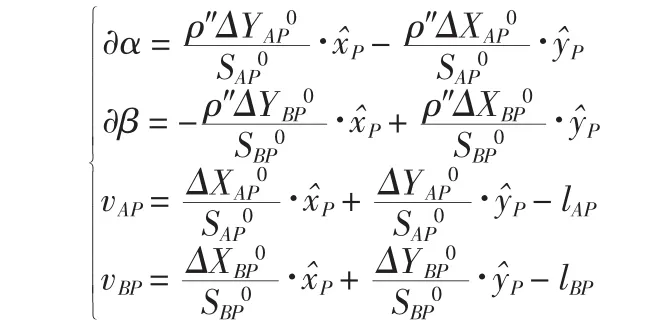
其中,lAP=LAP-,lBP=LBP-可由其近似坐标计算。
则基于最小[VTPV]=min,解算方程组V=BX-L
其解为:
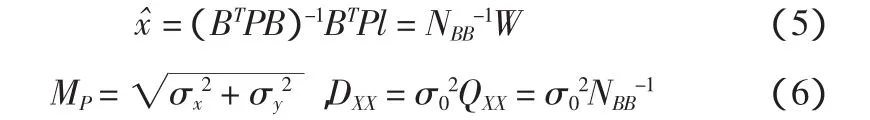
1.2 极坐标法
若A、B连线方位为A0,同时获得全站仪到P距离SAP,则可以计算其坐标(xP,yP)。
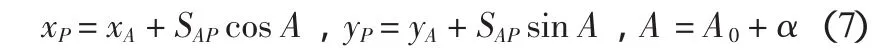
对上式全微分可得点位误差
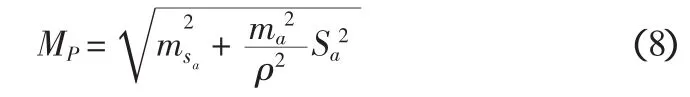
式中:msa为测边误差;ma为测角误差。
1.3 棱镜高程确定模型及其误差模型推导
基于三角高程测量,两已知点同时观测棱镜得到相应的SAP、δAP、SBP、δBP,则根据几何关系,P的高程h为:

2 测量定位方法选择
为获得适合实际工程应有的最优测量定位方法,以下从理论和实践两方面分析各定位方法的精度和实施方法。
2.1 理论分析
根据以上理论研究给出的各方法的式(2)、(4)、(6)、(8)和(10)定位误差模型,可以看出,定位精度与其各自的观测元素精度密切相关,下面分析各自的定位精度。
1) 边角交会法观测元素多于其他定位方法,又借助平差获得最终定位解,存在多余解。因此,同等精度观测元素情况下,其定位精度从理论上将明显高于其他定位方式。
2) 全站仪测量中,距离测量精度由常测量误差和比例测量误差组成,随着测量距离的增加,所有测量方法的测量定位精度将随之降低。
3) 角度是影响定位的非常重要的因素,从模型中还可以看出,对于交会法,全站仪和棱镜构成的三角形几何强度也是影响定位精度的另一个重要因素。可以证明,三点所构成的锐角三角形的定位精度要高于钝角三角形。
4) 定位耗时对于管节动态施工测量定位非常关键。若只有两台全站仪完成两个测量塔棱镜的定位,则在所有的定位方法中,极坐标法测量元素最少,1台全站仪实现1个棱镜的动态定位,定位耗时小;而其他定位方法测量元素较多,需要完成1个棱镜的交会定位后,旋转到另1个棱镜再实施定位,完成整个棱镜定位时间相对较长。因此,实际作业时,需要考虑定位时间与管节沉放作业速度之间的关系,确保定位精度。
2.2 试验及分析
为检验上述研究及理论分析的正确性,在一个实际工程中开展了相关验证试验。
试验中采用的全站仪为Leica TCA2003,测角精度为±0.5″,测距精度为1 mm+10-6mm,综合精度可以达到10 mm以内。为方便比较几种平面定位方法的精度,在此假设目标点在已知两点的中垂线上,即到两已知点的距离相等20°≤γ≤170°。根据以上定位误差模型,不同定位方法的定位精度如表1~表3所示。
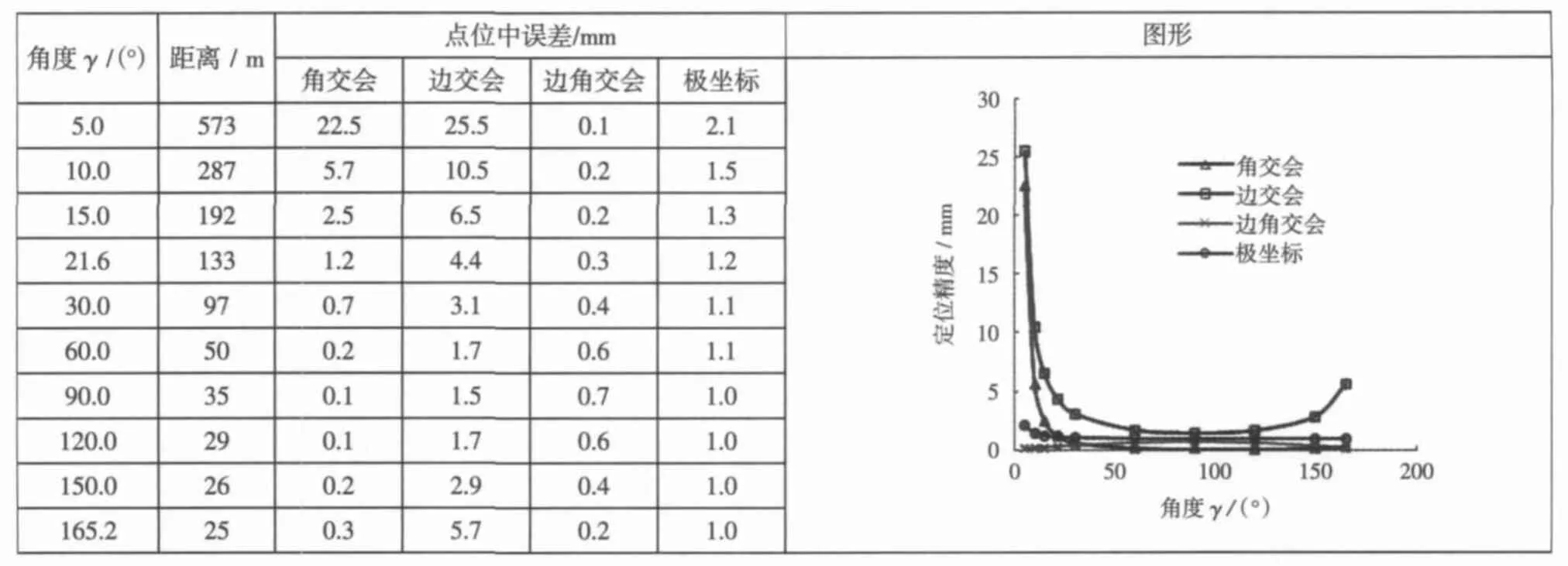
表1 SAB=50 m四种方法的点位中误差
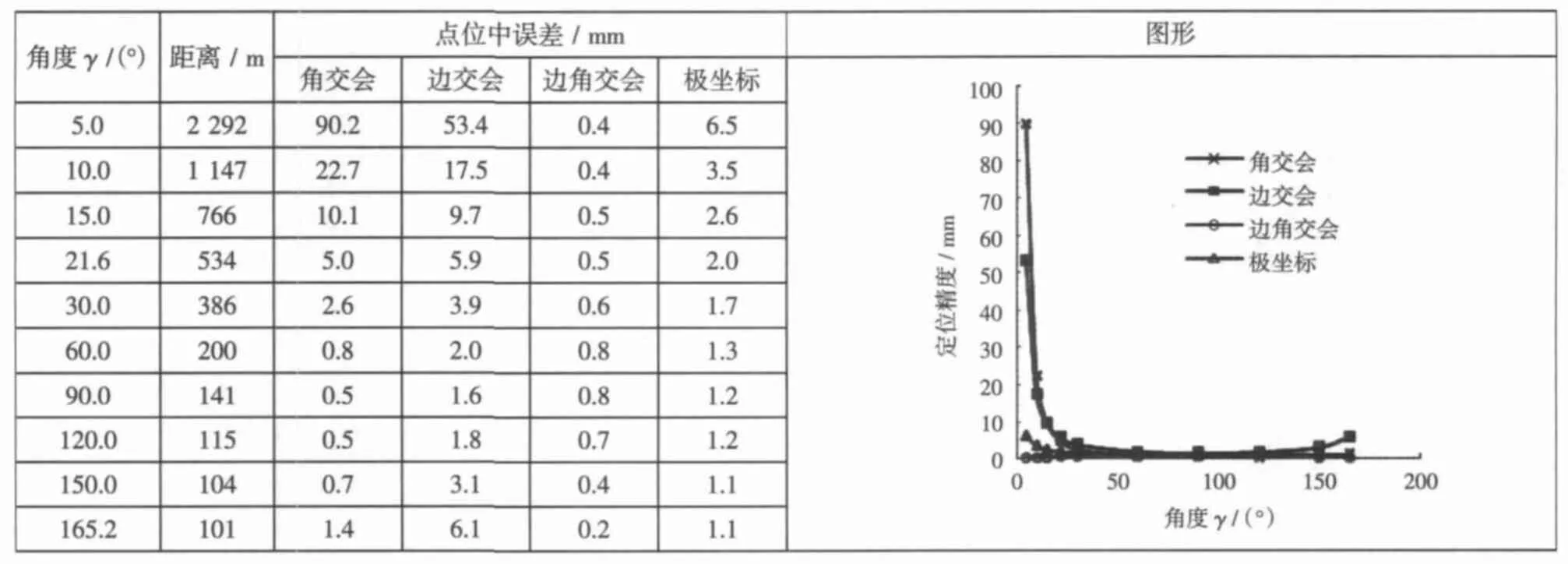
表2 SAB=200 m四种方法的点位中误差
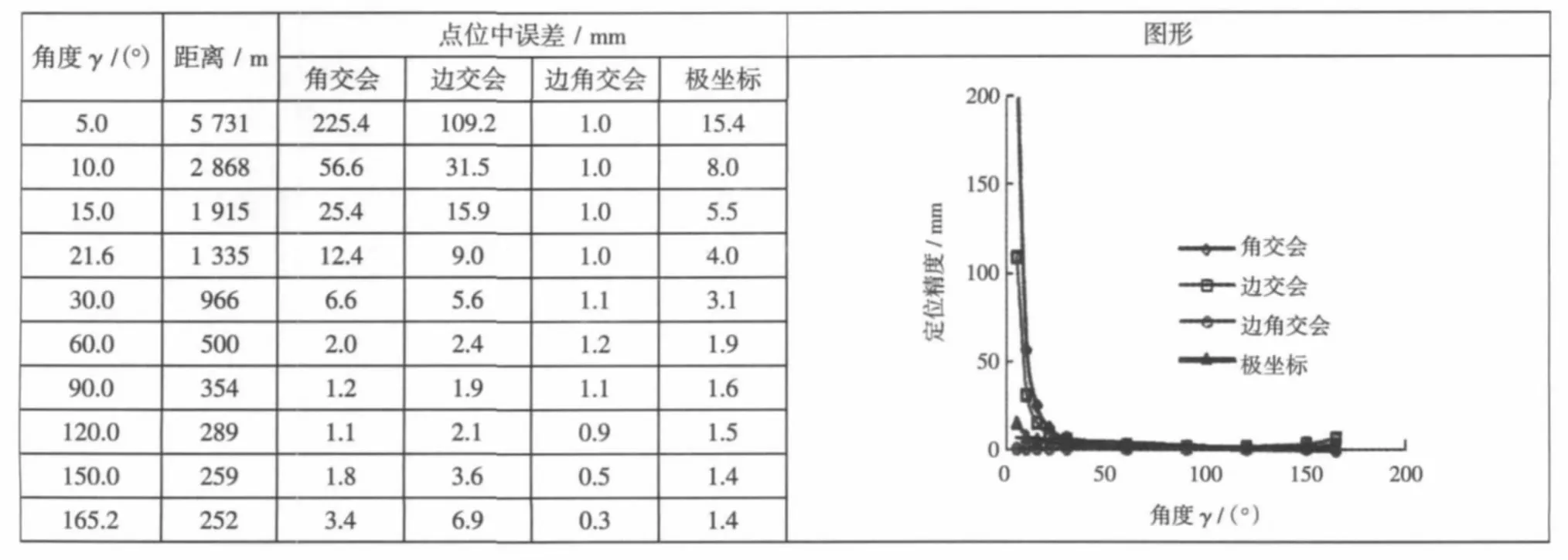
表3 SAB=500 m四种方法的点位中误差
可以看出:
1) 无论已知点间距离多大,两已知点与棱镜构成的锐角三角形图形定位精度最高,这也验证了上述理论分析的正确性。
2) 已知点交会棱镜点交角30°≤γ≤150°时,无论何种方法,定位精度均优于1.5 cm。
3)已知点到棱镜的作用距离小于1 000 m时,无论何种方法,定位精度均优于1.5 cm。
4) 在所有的4种定位方法中,边角交会精度最高,其次极坐标法和角交会法,精度最差的为边交会法。
5) 根据高程定位误差模型,对不同距离下的高程定位精度、测量塔水面上高度随垂直角的变化进行计算,如图2所示。
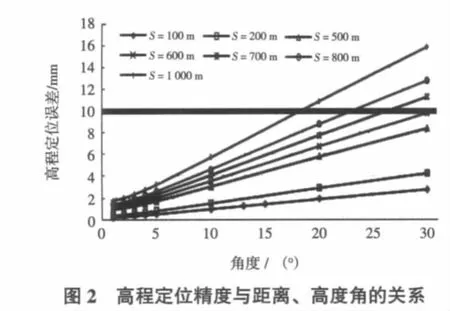
从图2可以看出,随着高度角的增加,距离的增大,高程测量精度降低;高度角小于30°,作用距离小于600 m时,高程测量精度优于10 mm;高度角20°时,距离0~1 000 m,高程测量精度均能满足11 mm精度要求。
综上,可认为在满足最大作用距离1 000 m时,基于三角高程测量方法获得的最弱高程测量精度为10 mm。
3 结论及建议
综上所述,给出如下结论和建议:
1)无论采用何种测量定位方式,作业距离小于1 000 m,全站仪间基线距离小于500 m,交会角度在30°≤γ≤150°之间时,4种测量定位方法均能够达到1.5 cm的综合定位精度,且4种定位方法定位精度由高到低的顺序依次为边角交会法、极坐标法、角交会法和边交会法。实际工程试验也验证了本条结论。
2) 为了进一步提高测量定位精度,建议采用交会法(边交会、角交会和边角交会)时,根据管节施工位置,合理选择安置全站仪的已知点位置,使得三者形成的三角形尽量为锐角三角形。
3) 尽管4种方法均能够满足测量定位的精度要求,但考虑管节施工中的沉放和对接作业为动态作业,若借助极坐标法实施观测,1台全站仪完全可以实现1个测量塔上的棱镜定位,期间由一个观测历元变换到另一个观测历元可在很短的时间内完成跟踪(如Leica TCA2003,跟踪时间0.3 s),其定位时间影响可以忽略不计;而对于其他测量定位方法,不但要实现同一个棱镜在管节动态变化过程中的跟踪,还有实现从当前棱镜到管节另一端的棱镜跟踪,期间距离和角度变化相对较大,跟踪耗时将比较大。此外,管节施工作业中,力求定位严格同步,即需要根据管节首尾测量塔上棱镜的同步位置,实现管节姿态、方位、三维位置的实时监控,基于两台全站仪的交会法显然难以办到,虽然4台全站仪可以实现,但需要仪器设备太多。因此,建议在实际作业过程中,采用极坐标法实现定位。
[1]GB 50026—2007,工程测量规范[S].
[2] 丁美,潘永仁.沉管隧道测量技术[J].现代隧道技术,2005(1):14-18.
[3] 何保喜.全站仪测量技术(1版)[M].郑州:黄河水利出版社,2005.
[4]常翔,张献伟.生物岛——大学城沉管隧道工程重难点浅析[C]//水底隧道专题技术交流大会论文集.北京:中国中铁隧道集团,2007.
