渤海海洋溢油的数学模型

李大鸣，刘江川，吴 丹，白 玲

渤海海洋溢油的数学模型

李大鸣1,2，刘江川1,2，吴 丹3，白 玲1,2

(1. 天津大学建筑工程学院，天津 300072；2. 天津大学水利工程仿真与安全国家重点实验室，天津 300072；3. 天津普泽工程咨询有限责任公司，天津 300204)

建立了嵌套模式的渤海二维水动力数学模型，模型网格采用显隐交替有限差分格式(即ADI差分格式)进行计算. 用追赶法逐段求解，用调和分析法计算模型的水动力边界条件，将潮汐过程计算结果与实测资料进行对比验证其结果吻合良好．溢油数学模型理论公式考虑了实时风场和表面流场作用下油膜质心的迁移和扩散范围，模拟了海上溢油油膜运动轨迹，并用水槽实验验证了公式的正确性．在水动力模型基础上应用溢油运动模式建立了海洋溢油数学模型，对风场作用和无风作用两种条件下的静止点源瞬时溢油和连续溢油运动轨迹和扩散范围进行了计算、分析和比较，并计算了有、无风场作用时移动点源连续溢油污染扩散范围，为海洋溢油数学模型的研究提供了较完整的思路．

海洋溢油；数学模型；渤海；显隐交替有限差分格式；溢油运动模式

渤海海域周围不仅有天津、秦皇岛、唐山、东营等城市，还有胜利油田、大港油田等这些非常重要的能源生产基地．随着环渤海区经济的快速发展，渤海海域环境恶化也日渐严重，其中溢油污染就是其中一个重要方面[1]．建立海上溢油行为及归宿数学模型，模拟突发性溢油事故后油膜的扩展、漂移过程，分析和预报石油污染范围，对科学制定应急抢险决策、把溢油损失降至最低具有十分重要的意义．

欧美国家从20世纪60年代开始对海上溢油进行预测，并发展了许多模式．费伊[2]模型考虑了平静水面上的溢油运动；武周虎等[3]模型提出了同时考虑油膜扩展和扩散作用以及油膜边缘的消失过程，得到了油膜扩延范围的计算公式；刘肖孔等[4]的扩展模型是在前人经验的基础上得出的一个描述油膜扩展3阶段的统一表达式[4]；布罗克尔[5]扩展模式和费伊扩展模式一样，描述的也是实验室条件下的溢油扩展过程，其中忽略了风场和流场的作用，忽略黏性力和表面张力的作用，只考虑重力作用的影响；蒙特卡罗方法扩展模式，又称随机抽样技巧或统计实验法，是通过运用溢油扩展预测程序显示溢油归宿轨迹[6]；Navy模型考虑了河流入流、潮流、地球自转流和风漂流作用[7]；张永良等[8]的模型考虑了油膜扩展和扩散过程中体积的衰减等．还有很多学者在这个方面研究并做出了贡献，例如熊德琪、杜川等[9]的溢油应急预报系统，金梅兵[10]的全动力溢油预测方法，娄安刚、吴德星[11]三维溢油模型的探索，杜怀勤、孙华[12]气相色谱法在海上溢油模型中的应用，李大鸣等[13]对油膜扩展公式进行了较为详细的推导和验证．

本文从水动力模型出发，对海洋模型边界、加密模型边界、风场作用的静止点源的瞬时和连续溢油的过程、移动点源的连续溢油过程进行了较系统和较全面的研究，提供了建立海洋溢油数学模型的较完整的思路．

1 海上溢油数学模型的理论基础

1.1 水动力数学模型理论

海上溢油的漂移与扩展主要取决于海面风场、流场和波的综合作用，所以建立一个高精度、高效率和良好稳定性的风海流、潮流水动力模式是海上溢油环境预测的前提．

1.1.1 基本方程及其离散

假定沿水深方向的动水压强符合静水压强分布且把水体看作是均质不可压的，通过垂向积分可以得到沿水深平均的流体运动基本方程．

连续方程为

运动方程为

式中：ξ为增水位；平均振幅Hhξ=+；h为平均水深；C为谢才系数；ρ为水的密度；u、v分别为x和y方向深度的平均流速；uf和vf均为柯氏系数；g为重力加速度；,sxτ、,syτ分别为x和y方向的海面风应力．由于潮流流速不大，本文忽略了黏性项．

采用显隐交替有限差分格式(alternating direction implicit，ADI)法对方程进行离散求解．差分交错网格为正方形网格，网格线分别平行于x轴和y轴，间距Δx=Δy=Δs ．运用显隐交替计算方法，解出每个时间步长上各点x、y方向上的流速和水深．

1.1.2 水边界的确定

模型中用调和分析的方法来确定水边界．潮汐调和分析是根据潮汐观测资料计算各个分潮的调和常数．任意一个分潮，可以表示为

式中：f为对平均振幅H的修正值；σ为角速度；Φ0为分潮的相角；φ为分潮交点订正角；角度为0时余弦函数取得最大值，所以σt+Φ0+φ=0°时发生高潮．实测资料显示实际情况并非如此，高潮一般要滞后一段时间发生，因此必须引入一迟角K′，即为

式中H、K′均由海区的深度、地形、沿岸外形等自然条件决定．任意时刻的潮位

式中：a0为平均海平面高度；j为分潮的序号；m为总的分潮数；fj为分潮的交点因子；Hj为分潮的振幅；σj为分潮角速度；(Φ0+φ)j为分潮的天文初相角；gj为分潮的专用迟角．

1.1.3 潮汐过程

本文采用最小二乘法来分析潮汐过程[14]，基本思想如下所述．

取计算所得的潮位为

用来逼近实测的潮位()tζ．按照最小二乘法原理，必须使

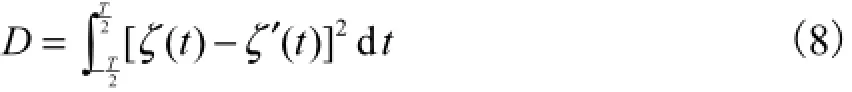
最小，以此来确定系数aj和bj．把式(7)代入到式(8)，可得

求D对a0、aj、bj的偏导数，且令其等于0，这时附标为j的项为指定分潮，即所欲求的分潮．

1.2 溢油数学模型理论

1.2.1 溢油扩展

油膜表面的蒸发量Fv为

式中：T0为修正蒸馏曲线的初馏点；TG为修正蒸馏曲线的斜率；Te为周围温度；θ为蒸发暴露系数；S( t)为t时刻海上溢油面积；A、B均为常数，一般取A=6.3，B=10.3．

油膜表面的乳化量Fw为式中：C1、C2分别为吸水率和包水率，一般取C1=2.0× 10-6，C2=1.33；uF为海面风速；Q( t)为抵岸油量．

油膜扩展第1阶段——重力扩展阶段的油膜扩展半径为

在油膜扩展第2阶段，油膜位能和黏性阻力起主要作用，由油膜位能与黏性阻力平衡得到

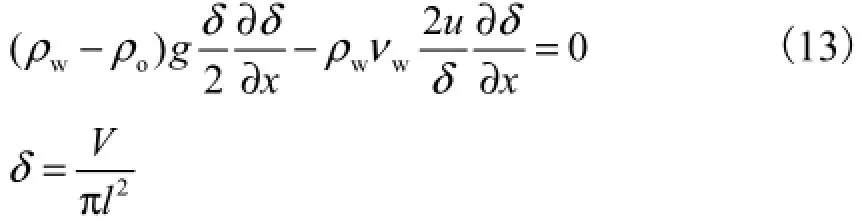
式中：oρ、wρ分别为油和水的密度；wν为水的运动黏性系数；δ为油膜厚度；V为溢油体积；l为油膜扩展半径．

整理方程，得到重力-黏性力扩展阶段油膜扩展半径在油膜扩展达到第3阶段时，黏性力与表面张力

平衡，即

式中β为水、油、气的净表面张力系数．

表面张力-黏性力扩展阶段的油膜扩展半径

本文通过实验对油膜扩展公式进行了验证．实验中，水槽长和宽分别为60,cm、25,cm，水流平均流速约为0.04,m/s．其模拟结果与实测对比如表1所示．

表1 模拟结果与实测值比较Tab.1 Comparison between the simulated values and the experimental values

1.2.2 油膜漂移

风场和表面流场作用是油膜漂移的主要动力，如图1所示．

图1 迁移速度矢量合成Fig.1 Vector synthesis of migration velocity

波浪作用下，油膜漂流速度ru的表达式为

表面流速项

风场项

式中：K1为表面流速的修正系数，它综合考虑了油膜的内应力、厚度等多种因素对表面流速的影响，可通过经验公式来确定，一般取1.0；uc为海面流速，由渤海水动力数学模型确定；K2是风场项的修正系数，由经验公式确定；uf是海面实时风速，通过对实测资料进行插值得到．

1.2.3 溢油运动模型

海上溢油的运动主要由油膜的扩展和油膜的漂移两部分组成．考虑油膜扩展的随机性，溢油运动数学模型中应该还有一个随机量．假设油膜某质点在ti时刻的坐标位置为R(ti)，ti+1时刻的坐标位置为R(ti+1)，R表示质点在油膜扩展、漂移等因素下移动的距离，则有

式中：sR为油膜质点在tΔ时间段内的扩展矢量；lR为油膜质点在tΔ时间段内的漂移矢量；γ为随机数，取值为-1～1．

2 渤海海洋溢油数学模型

2.1 模型参数

为了提高水动力模型的计算精度，采用大模型与小模型嵌套的数学模型．采用自动划分、逐级加密、分区优化的方法进行网格剖分．大模型为小模型提供边界，从而得到渤海海域流场分布详图和潮位曲线．大模型计算域为E,117°38'47"～E,126°32'38"和N,35°18'5"～N,40°50'43"．小模型在大模型中的位置如图2所示，A点位于E,122°35'24"、N,39°32'35"，B点位于E,122°35'24"、N,39°26'5"；AB左侧为小模型区域．大小模型均采用正方形网格剖分计算区域．大模型空间步长10,km，时间步长60,s，剖分后网格为78列×61行．小模型空间步长2,km，时间步长3,s，剖分后网格为205列×215行．模型网格如图3所示．

图2 小模型在大模型中的位置Fig.2 Location of the small-scale model in the large-scale model

采用调和分析法确定大模型边界条件，根据2002年3月1日0时—2002年12月31日23时的青岛港潮位资料计算出调和常数，从而计算出大模型的边界潮位．计算结果与实测资料的比较如图4所示，结果吻合良好．

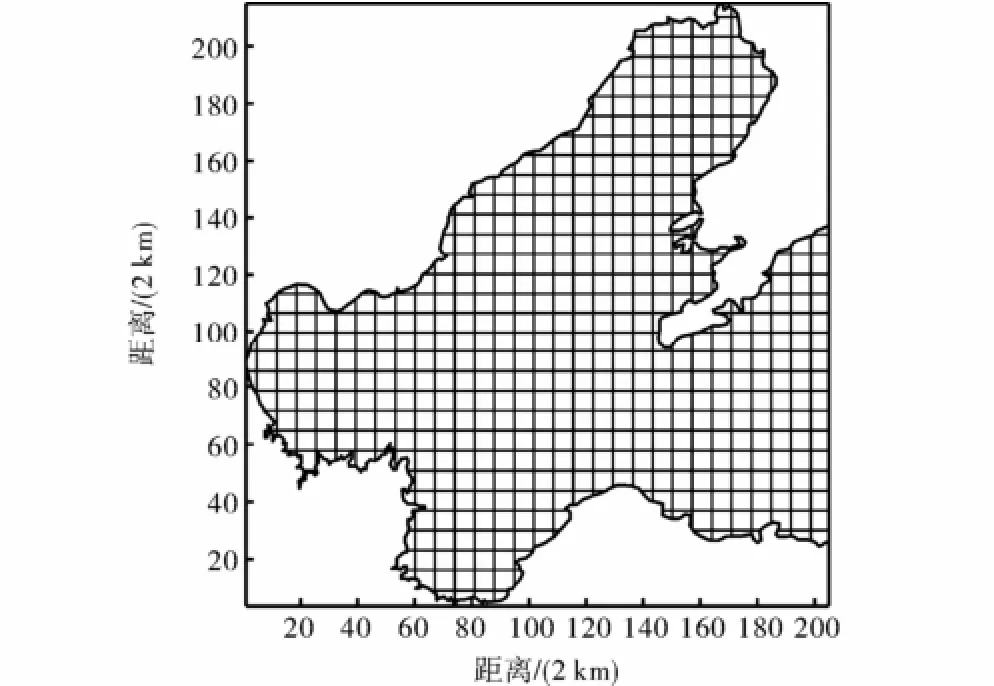
图3 小模型网格剖分结果Fig.3 Small-scale model grids

选择2009年8月10日8时—8月14日8时青岛港调和分析的潮位过程作为大模型的边界条件，计算出大模型在96,h内的潮位和流速变化过程．由大模型的计算结果提取出图2中A、B两点的潮位过程线，通过小模型计算得到渤海潮汐变化过程和逐时潮流流场．小模型计算结果与塘沽站的潮位曲线比较结果如图5所示，大模型第32小时流场如图6所示，小模型第32小时流场如图7所示．从图5可以看出，塘沽站计算与理论天文潮比较吻合较好，图6和图7潮流场基本合理，表明渤海水动力数学模型成果可以作为海洋溢油数学模型的动力条件．

图4 大模型潮位Fig.4 Tide level in large-scale model

图5 天文潮潮位小模型验证结果Fig.5 Astronomical tide validation of the small-scale model

图6 第32小时大模型流场示意Fig.6 Flow field of the large-scale model at 32,nd hour

图7 第32小时小模型流场示意Fig.7 Flow field of the small-scale model at 32nd hour

2.2 结果与分析

本文溢油量是按照油轮灾难性溢油事故的最大溢油量设定的．静止点源瞬时溢油溢油量设定为7,200,t，选择了曹妃甸海域的一个溢油点，具体信息见表2和表3．

表2 溢油基本信息Tab.2 Information of the oil spill spot

表3 油的性质Tab.3 Properties of the oil

模型中的风场采用MM5提供的风场实测资料，取2007年8月11日8时—2007年8月14日8时的实时风场．利用水动力数学模型计算得到流场，模型主要模拟了以下几种溢油形式．

1) 静止点源瞬时溢油

静止点源瞬时溢油是在某个特定位置溢油量大且溢油时间很短的溢油方式．以曹妃甸附近海区某静止点源瞬时溢油为对象研究污染范围区，考虑有风和无风两种情况．图8和图9分别给出了风场作用下和无风情况下静止点源瞬时溢油72,h的油膜污染范围局部放大图．

图10为有风及无风作用下静止点源瞬时溢油在72,h内油膜质心漂移轨迹．曹妃甸地区地处东亚季风气候区，本文选取的时段是2007年8月中旬，夏末秋初多风季节，因此在整个溢油过程中，风速对油膜扩展漂移的影响较大．溢油漂移扩散过程随风速变化可分为4个阶段：第1阶段为东南风，约从第1小时到第6小时；第2阶段为东北风，约从第7小时到第32小时；第3阶段为西南风，约从第33小时到第45小时，第4阶段为西北风，约从第46小时到第72小时．

溢油发生后，油膜在流场和风力的作用下漂移、扩展，污染面积逐渐增大．通过追踪油膜72,h内的行为，得到溢油发生72,h内油膜的行为状态和海洋污染范围．溢油发生时落潮，在无风条件下，溢油随着表面潮流向东南方向漂移，然而受到东南风的作用，油膜整体向西北方向移动．第2次落潮时，在东北风的作用下，由于此阶段风速比表面潮流流速大得多，油膜迅速西南移动．第3次落潮时，受到西南风的作用，油膜向东北方向移动．最后阶段在东北风的作用下，油膜又向回漂移．由于风作用比流速作用大得多，所以油膜整体上是随风向运动的．

图8 风场作用下油膜72,h污染范围Fig.8 Polluted area in 72,h affected by the wind

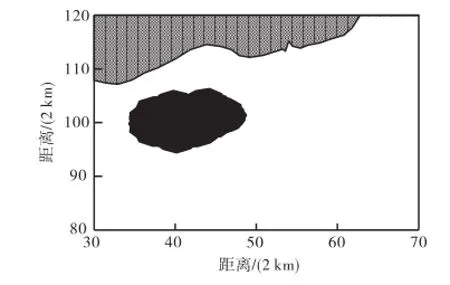
图9 无风油膜72,h污染范围Fig.9 Polluted area in 72,h without wind

图10 有风和无风作用下漂移轨迹比较Fig.10 Comparison between the barycenter trajectory with and without wind effect

2) 静止点源连续溢油

静止点源连续溢油模式常见于船舶油仓泄漏、岸上储油罐破损后漏油、海上钻井平台井喷、海底石油管道破裂等引起的海洋溢油．与等溢油量静止点源瞬时溢油相比，溢油持续时间较长，但单位时间溢油量较少，故溢油扩散范围也较小．图11给出了风场作用下和无风情况下静止点源连续溢油油膜72,h质心漂移轨迹．

3) 静止点源瞬时溢油与连续溢油比较

静止点源瞬时溢油，如油轮触礁储油罐破损严重、大量油品迅速泄露等情形，油膜一般会迅速扩延，但是后期扩大趋势不明显．而静止点源连续溢油，如船舶撞击导致油仓泄油，这种形式的溢油油膜扩展速度相对较慢，但持续时间较长．从污染范围看，溢油量相同的情况下，瞬时溢油的污染面积较连续溢油污染面积大．当溢油总量为7,200,t时，在风场作用下，瞬时溢油扫海面积约1,187,km2，而连续溢油扫海面积约478,km2．图12给出了无风、风场作用下静止点源瞬时溢油与连续溢油的油膜扩散范围比较.

4) 移动点源连续溢油

移动点源连续溢油的情况很常见，如船舶在航行过程中漏油，又如行进中的船舶排污水等，一般经过一段时间以后就会沿着船舶行驶的方向形成狭长的溢油带；离开船舶愈远溢油带愈宽，在潮流和风速作用下溢油带会出现摆动和聚散．移动点源连续溢油数学模型的建立一般以静止点源连续溢油计算模式为基础．当油轮以0.5,m/s的速度由西向东行驶、溢油总量7,200,t、溢油速度0.03,m3/s时，分别计算了有风、无风两种情况下72,h内的油膜污染范围，风向以东北偏北风为主，计算结果如图13所示．

图11 静止点源连续溢油油膜质心漂移轨迹Fig.11 Barycenter trajectory of the continuous oil spill from static point source

图12 静止点源瞬时溢油与连续溢油扩散范围比较Fig.12 Polluted area comparison between instantaneous and continuous oil spill from static point source

图13 移动点源连续溢油扫海面积Fig.13 Polluted area of the continuous oil spill from moving point source

通过比较可以看出，无风情况下移动点源连续溢油运动轨迹与油轮运动轨迹总体相一致但略有偏移，偏移量是因潮汐作用引起的；在风场作用下，移动点源溢油运动轨迹沿油轮运动方向在无风情况的偏移量基础上呈游荡型扩散，此阶段溢油运动不仅受到潮汐作用影响，同时与模型风场的大小和方向变化过程有关．油轮自西向东航行，溢油在海上扩散时间愈长，溢油带愈宽，同时受到溢油区变化风场的影响，使得溢油带总体在扩散的同时发生漂移．

3 结 论

(1) 建立了渤海水动力模型，模型主体网格采用ADI差分格式进行显隐交替计算，模型的水动力边界条件用调和分析法计算求得，将潮汐过程计算结果与实测资料进行对比验证，结果吻合良好．溢油扩展公式和溢油漂移公式考虑了实时风场和流场作用下油膜质心的迁移，模拟出海上溢油油膜运动轨迹，并用水槽实验验证了模型的正确性．在水动力模型基础上应用溢油运动模式建立了海洋溢油数学模型，为研究海洋溢油数学模型提供了较完整的思路．

(2) 应用海洋溢油数学模型详细计算了风场作用与无风两种条件下静止点源瞬时溢油和连续溢油油膜质心运动轨迹和扩展范围；以静止点源连续溢油计算模式为基础，计算了风场作用和无风两种情况下移动点源连续溢油的扫海面积．计算结果为针对不同类型的海洋溢油事件的应急处理与回收工作提供了重要的理论依据．

(3) 计算结果分析表明，风场作用扩大了溢油污染范围，在总溢油量相等和相同的风场条件下，静止点源瞬时溢油扩散范围大于静止点源连续溢油扩散范围．比较静止点源连续溢油和移动点源连续溢油这两种情况的计算结果可以看出：无风情况下，移动点源连续溢油油膜沿着油轮运动轨迹扩散，并受潮汐作用有所偏移；加入风场作用后，受风向和风力大小的影响，油膜扩散轨迹随风场摆动，溢油污染范围扩大．

［1］ 于 挺. 海上油田溢油事故的影响及处理决策分析[J]. 石油化工应用，2007，26(6)：53-56.

Yu Ting. The influence of offshore oilfield oil spill and its decision analysis[J]. Petrochemical Industry Application，2007，26(6)：53-56(in Chinese).

［2］ Fay J A. Physical processes in the spread of oil on a water surface[C]// Proc Conf Prevention and Control of Oil Spills. Washington DC：American Petroleum Institute，1971：463-467.

［3］ 武周虎，尹海龙. 水面有限长油膜下油滴浓度分布及其污染带的数值计算[J]. 水动力学研究与进展：A辑，2001，16(4)：481-486.

Wu Zhouhu，Yin Hailong. Concentration distribution of oil droplets beneath a finitely-long oil slick at water surface and pollution zone[J]. Journal of Hydrodynamics：Series A，2001，16(4)：481-486(in Chinese).

［4］ Liu Shiao-Kung，Leendertse J J. A 3-D oil spill model with and without ice cover[C]//Proc of the Internal Symposium on Mechanics of Oil Slicks. Paris，France，1981：1-32.

［5］ Blokker P C. Spreading and evaporation of products on water[C]// Proc of 4th Internal Harbour Congress. Ant-werp，the Netherlands，1964：910-920.

［6］ 娄安刚，王学昌，于宜法，等. 蒙特卡罗方法在海洋溢油扩展预测中的应用研究[J]. 海洋科学，2000，24(5)：7-9.

Lou Angang，Wang Xuechang，Yu Yifa，et al. Studies on Monte-Carlo method application for predicting marine oil spill diffusion[J]. Marine Science，2000，24(5)：7-9(in Chinese).

［7］ Reed M，Johansen O，Brandvik P J. Oil spill modeling towards the close of the 20th century：Overview of the state of the art[J]. Spill Science and Technology Bulletin，1999，5(1)：3-16.

［8］ 张永良，褚绍喜，富 国，等. 溢油污染数学模型及其应用研究[J]. 环境科学研究，1991，4(3)：7-17.

Zhang Yongliang，Chu Shaoxi，Fu Guo，et al. Study on the mathematical model of oil spill pollution and its application[J]. Research of Environmental Sciences，1991，4(3)：7-17(in Chinese).

［9］ 熊德琪，杜 川，赵德祥，等. 大连海域溢油应急预报信息系统及其应用[J]. 交通环保，2002，23(3)：5-7.

Xiong Deqi，Du Chuan，Zhao Dexiang，et al. Oil spill modeling information system for Dalian sea and its application[J]. Environmental Protection in Transportation，2002，23(3)：5-7(in Chinese).

［10］ 金梅兵. 近岸溢油的全动力预测方法研究[J]. 海洋环境科学，1997，16(1)：30-36．

Jin Meibing. Study on the method of the dynamical prediction of spill oil inshore[J]. Marine Environmental Science，1997，16(1)：30-36(in Chinese).

［11］ Lou Angang，Wu Dexing. Establishment of a 3D model for oil spill prediction[J]. Journal of Ocean University of Qingdao，2001，31(4)：473-479.

［12］ 杜怀勤，孙 华. 气相色谱法在海洋溢油鉴别中的应用研究[J]. 油气田环境保护，2001(2)：38-40.

Du Huaiqin，Sun Hua. Research on the application of method of gas chromatography for distinguishing oil spillage in the sea[J]. Environmental Protection of Oil and Gas Fields，2001(2)：38-40(in Chinese).

［13］ 李大鸣，陈海舟，付庆军. 海上溢油数学模型的研究与应用[J]. 哈尔滨工程大学学报，2008，29(12)：1291-1297.

Li Daming，Chen Haizhou，Fu Qingjun. Research and application of mathematical modeling to oil spills on the sea[J]. Journal of Harbin Engineering University，2008，29(12)：1291-1297(in Chinese).

［14］ 孔 俊，宋志尧，张金善，等. 风暴潮模拟中潮位对风拖曳力系数的影响研究[J]. 海洋预报，2008，25(1)： 74-79.

Kong Jun，Song Zhiyao，Zhang Jinshan，et al. Research of the effluence of tidal level on wind drag stress coefficient in storm surge model[J]. Marine Forecasts，2008，25(1)：74-79(in Chinese).

Mathematical Model of Marine Oil Spill in Bohai

LI Da-ming1,2，LIU Jiang-chuan1,2，WU Dan3，BAI Ling1,2
(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，Tianjin 300072，China；3. Tianjin Pu Ze Engineering Consulting Company Limited，Tianjin 300204，China)

A two-dimensional nested regional hydrodynamic model of Bohai was established，in which alternating direction implicit(ADI)method was applied in discrete shallow water circulation equation and chasing method was applied in solving equation groups. The water border of the model was defined by the method of harmonic analysis，and the calculation result matched well with measured values. Oil spill schema adopted in the model described the path of the center of the spilled oil by the effect of wind and flow fields，and the result was validated in a water channel experiment. Mathematical model of marine oil spill was set up based on the hydrodynamic model and oil spill schema. Instantaneous and continuous oil spill from static point source were calculated with and without wind field，then continuous oil spill from moving point source was simulated. This mathematical model provided a complete exemplification for research on oil spill on the sea.

marine oil spill；mathematic model；Bohai；ADI method；oil spill schema

TV92

A

0493-2137(2012)01-0050-08