基于非线性静、动力方法的RC简支梁桥连梁装置参数优化研究

江 辉，李 宇，熊智阳，杨庆山，朱 晞，倪永军

(1.北京交通大学 土木建筑工程学院，北京 100044;2.长安大学 公路学院，西安 710064;3.长沙市轨道交通集团有限公司，长沙 410007)

在破坏性地震中，桥梁上部结构的纵向移位和落梁破坏是最为常见的震害之一［1］，坠落的梁体如果撞击桥墩，还会给下部结构带来更大的破坏。如在1989年的美国Loma Prieta地震中，旧金山奥克兰海湾大桥上的一跨大跨度简支钢桁梁桥发生了落梁震害;在1994年的Northridge地震中，许多桥梁因落梁而丧失使用功能;在1995年的日本阪神地震中，阪神地区超过60%的桥梁遭到破坏，主要原因就是由于支座和约束构件失效后梁体发生很大的移位，甚至落梁;在2008年我国四川的5.12汶川地震中，落梁也是最为严重的桥梁破坏类型之一。

基于对桥梁震害的反思，国际地震工程界展开了深入研究，连梁装置被认为是防止简支梁桥或连续梁桥联、联之间落梁的一种有效措施［2－5］。国内学者也展开了系统研究，朱晞、王根会等［6］针对16 m跨铁路简支梁桥提出了一种由高强钢筋和橡胶块组成的纵向连接装置;朱文正、刘健新［7－8］考虑桥梁重要性分类、地震动参数和桥梁地震荷载重要性系数提出了连梁装置的设计方法;王军文、李建中等［9－10］考虑相邻桥跨不同向振动的动力特性以及相邻梁体间碰撞对相对位移的影响，提出了一种限位装置的设计方法。在规范方面，我国现行《铁路工程抗震设计规范》(GB 50111－2006)(2009年版)［11］和《公路桥梁抗震设计细则》(JTG/T B02 －01 －2008)［12］中，也提出了强震下设置连接限位装置的基本规定。

但是，各国学者的研究主要集中于连接装置设计荷载的确定以及不同连接装置下桥梁抗震效果的对比分析;相关规范也没有给出明确的设计方法，操作性不强，且未能反映新的桥梁震害现象的启示，难以指导实际桥梁的抗震设计。连梁装置的刚度取值对桥梁的整体抗震性能具有显著影响［3，13－14］，直接决定了不同设防烈度水平下的限位效果，以及地震力在墩、梁不同构件之间的分配。Priestley等［3］指出，如约束构件的刚度不足，其抗震效果难以实现，在一定范围内提高约束构件的刚度后有显著作用。Zhu［13－14］的研究也表明，如果采用合适的刚度和阻尼参数，约束构件可以有效减轻梁间碰撞，此外，当约束构件的刚度达到一定值后，其约束效果不会随着刚度而继续增加。上述研究成果表明，RC梁式桥的梁端连接装置存在合理的刚度范围，从而最大限度降低地震导致的大变形及碰撞效应。因此，深入研究不同场地条件和设防烈度下连接装置刚度对桥梁地震响应的影响程度及其规律，并探讨其合理取值，对于降低地震作用、保障强震下桥梁结构的安全具有重要意义。

在我国铁路工程中，90%以上的桥梁是简支梁桥，而简支梁桥又是抗震能力最弱的一种桥型，落梁破坏极易发生。本文以典型的铁路RC梁式桥为研究对象，分别采用基于FEMA440性能点轨迹法的非线性静力分析方法［15］，以现行《铁路工程抗震设计规范》设计谱及5.12汶川强震记录构建需求谱，研究了不同场地条件和设防烈度下连梁装置刚度对桥梁地震响应各项指标分布特征及其规律的影响机理，探讨了连梁限位装置刚度的合理取值，并采用非线性动力时程分析方法进行了验证。研究成果可供我国梁式桥的抗震设计及规范修编参考。

1 RC梁式桥纵向连接装置及模拟方法

1.1 橡胶－拉杆式连梁装置

梁式桥的抗震限位装置主要有两种类型，一类为连接式限位装置，包括梁、梁间连梁连接装置以及梁、墩(台)间连接装置;另一类为分离式限位装置，具体为平行、垂直于桥轴方向的挡块等。既有的资料表明，在众多的限位装置中，橡胶－拉杆式连接装置(如图1所示)应用得最为广泛。该装置主要由降低梁间碰撞作用的橡胶块、拉杆及连接锚具等三部分组成，拉杆通常由高强钢筋构成，拉杆装置的刚度可根据定义由下式计算:

式中，E为所用钢材弹性模量，A为连梁拉杆的截面总面积，L为连梁拉杆有效工作长度。对于不同场地和设防水平下的桥梁，所需的拉杆刚度可通过在一定范围内调整所用的拉杆直径、根数以及长度等主要参数来获取。为分析方便，将连梁拉杆装置的刚度进行无量纲化:

式中Km为伸缩缝处相邻梁体的线刚度，无量纲刚度比η在0～1范围内取值，其中“0”代表不设置连梁拉杆装置的情形，“1”代表连梁拉杆装置刚度和梁体线刚度相等的极端情况。

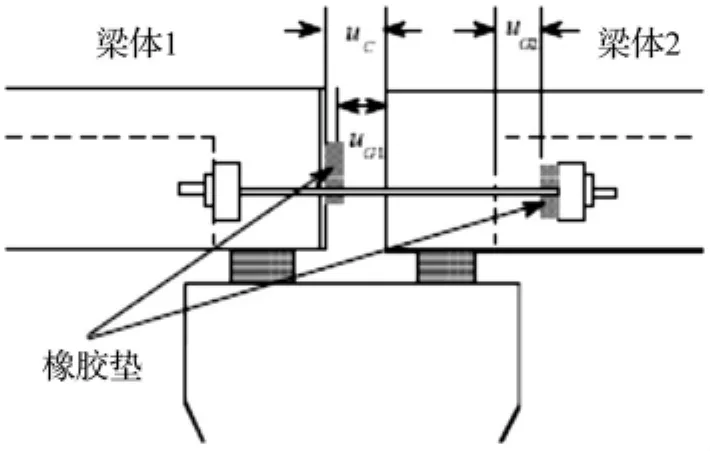
图1 橡胶－拉杆连梁装置详图Fig.1 Detailed drawing of rubber－ tie bar device

1.2 连梁装置的有限元模拟

对于橡胶－拉杆式连梁装置，其计算模型见图2。其中ΔG为梁端初始间隙，kk为梁间橡胶垫的碰撞刚度，c为装置的等效阻尼，s为限位装置的初始间隙(不工作长度)。当梁端相对位移超过初始间隙长度时，装置开始参与工作，其非线性力－变形关系为:

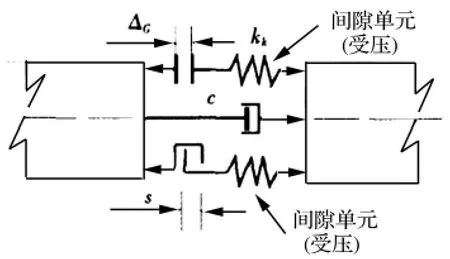
图2 安装连梁装置后梁间伸缩缝计算模型Fig.2 Computation model for expansion joint with unseating prevention device

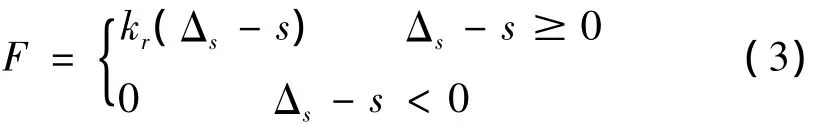
式中，F为连梁装置分担的地震力，初始间隙s在本文中取为20mm，Δs为地震作用下伸缩缝处相邻梁体的相对远离位移;kr为连梁装置刚度。本文中，采用SAP2000有限元软件中的Hook单拉单元模拟拉杆，采用GAP单压单元模拟梁端面降低碰撞作用的橡胶块。

2 桥梁有限元模型

2.1 桥梁概况

三跨(16 m+24 m+16 m)单线铁路简支梁式桥，梁体参考铁道部专业设计院编制的《超低高度后张法部分预应力混凝土梁》(专桥2090(16 m跨)、2091(24 m跨))，组合T型截面，梁体材料为C40混凝土，梁端初始间隙为60mm;桥墩为等截面矩形墩，截面尺寸为3.65×2.46 m，墩高20 m，桥墩材料为 C30 混凝土;支座采用盆式支座(固定支座)和板式橡胶支座(活动支座);梁端选用截面尺寸为250mm×150mm、厚度为40mm的橡胶垫，其抗压刚度Kk为2.5×104kN/m。桥台类型为U型桥台，按照简化方法建立弹簧约束单元模拟。RC混凝土的材料阻尼比为5%，动力分析时结构体系阻尼采用Rayligh阻尼计算。算例桥梁的有限元模型见图3。为了有效考虑土体和桥墩基础之间的动力相互作用，用“m”法计算等效土体弹簧参数，三个平动和转动方向的土弹簧刚度取值如表1所示。

图3 全桥有限元模型Fig.3 Finite element model of the bridge

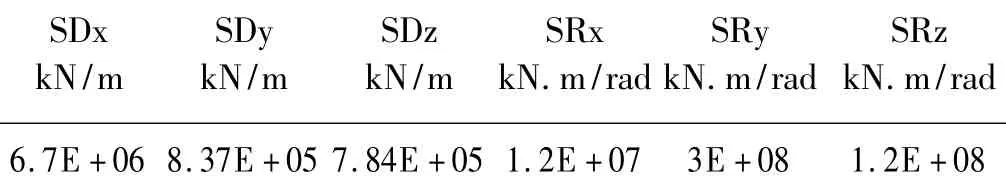
表1 墩底等效土弹簧刚度取值Tab.1 Equivalent spring stiffness of constraint soil at the bottom of piers

2.2 墩底截面弯矩－曲率分析

算例桥梁的墩底截面配筋布置如图4所示。为了保证墩底截面具备延性抗震能力，纵向钢筋采用HRB235钢(直径25mm)，配置96根，长边每边30根，短边19根，配筋率为0.53%;箍筋直径为12mm，间距为5 cm，加强区混凝土核心范围内，箍筋间主筋根数为3根，箍筋肢距为20 cm;墩底加强区域之外部位的箍筋间距为10 cm，均满足现行《铁路工程抗震设计规范》要求。利用UC－fyber软件对该截面进行弯矩－曲率(M～Φ)分析，所得到的滞回模型骨架曲线如图5所示，通过等效线性化得到墩底截面的屈服点和极限点。依据现行《公路桥梁抗震设计细则》［12］第 7.4.3 条规定，可算出墩底等效塑性铰长度为1.79 m。

图4 桥墩截面钢筋布置Fig.4 Arrangement of steel bars on cross section of the pier

图5 墩底截面弯矩－曲率关系Fig.5 Bending moment-curvature relation for the bottom section of piers

3 基于非线性能力谱方法的连梁装置合理刚度研究

3.1 采用性能点轨迹法的结构抗震性能求解方法

3.1.1 选取反应谱并将其转化为Ay(谱加速度)－Dy(谱位移)形式，作为5%阻尼比的初始弹性需求谱，由推倒分析得到结构的Pushover曲线，并进行双线性化将其转化为能力曲线。

3.1.2 根据 FEMA440 所提出的性能点轨迹法［15］，选取初始性能点，假定最大位移 dpi和加速度 api，按照ATC－40［16］的相关步骤，对能力谱曲线进行双线性化，进而得到等效SDOF系统的初始周期T0、屈服位移dy以及屈服加速度ay(上述参数将随初次假定的dpi和api而变化)，以此为基础计算结构延性μ及屈服后刚度比α，从而得到等效阻尼βeff、等效周期Teff、阻尼修正系数B(βeff)以及谱修正系数M。

3.1.3 利用阻尼修正系数B(βeff)对初始弹性需求谱进行折减，得到与βeff相对应的折减需求谱，通过谱修正参数 M对其进行修正，从而得到修正的需求谱(MADRS)。

3.1.4 可能的性能点即为代表割线周期Tsec的射线与修正的需求谱(MADRS)的交点。重复上述步骤即可得到一系列可能的性能点，确定性能点轨迹曲线，其与能力曲线的交点即为结构的实际性能点。性能点轨迹法的求解步骤见图6。

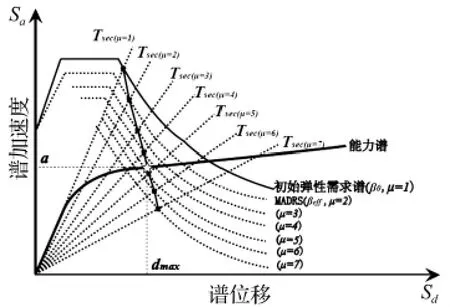
图6 基于修正需求谱的性能点轨迹曲线Fig.6 Trace curve of performance point based on MADRS

图7给出了按照上述方法计算设置了不同刚度连梁装置的桥梁的性能点求解模式。

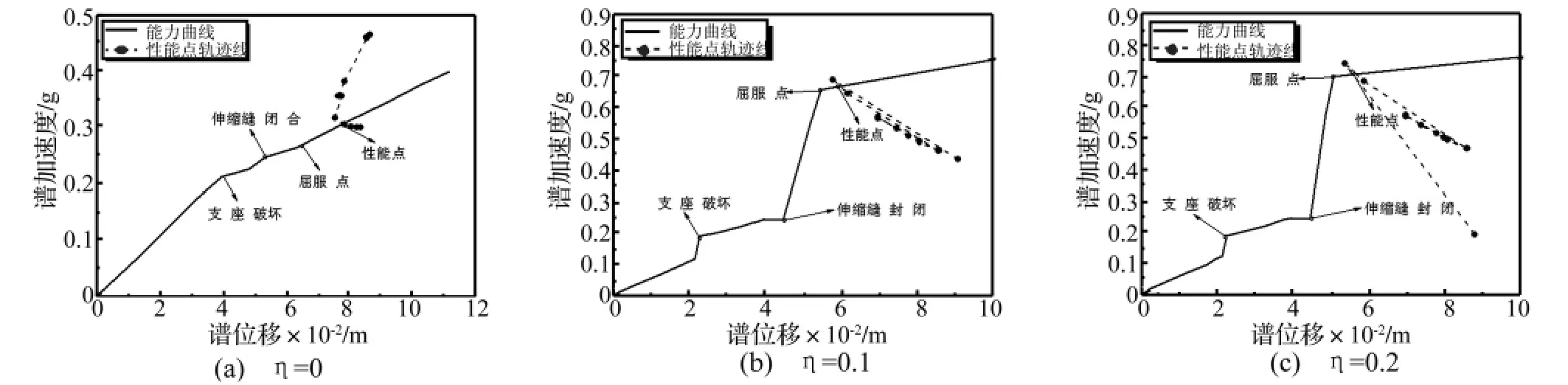
图7 设置不同刚度连梁装置的桥梁等效单自由度体系性能点Fig.7 Performance point of the bridge with unseating prevention device of different stiffness

3.2 不同场地下连梁装置刚度取值研究

对于我国铁路工程中广泛存在的简支梁桥，为了研究连梁装置的合理刚度，首先采用《铁路工程抗震设计规范》(GB 50111－2006)(2009年版)所给出的四类场地下的设计谱，经转换得到如图8所示的与规范相容的地震动需求谱(8度罕遇地震，PGA=0.38 g，阻尼比5%)，进行能力谱分析。

图8 不同场地条件下的需求谱曲线Fig.8 Demand spectra under different site soils

按照前述的性能点轨迹法，对于四类场地分别求解设定地震动水平下桥梁的性能点。对于非线性静力分析，可以获得和原桥梁相对应的等效SDOF体系的基底剪力和墩顶变形，以此二个指标为关键参数，代表桥梁的地震响应进行分析。图9和图10分别给出了不同场地条件下，当设防烈度为8度罕遇地震时，连接装置刚度对桥梁结构的墩顶位移和基底剪力的影响规律。从四类场地下桥梁地震响应指标的分布可看出，对于Ⅰ类场地(坚硬岩石场)，随着连梁装置刚度的增大，墩顶位移逐渐降低，基底剪力则不断增大，规律性显著;对于Ⅱ类场地(中硬场)，和Ⅰ类场地类似，随着连梁装置刚度的增大，墩顶位移逐渐降低，基底剪力不断增大;对于Ⅲ类场地(中软场)，基底剪力随着连梁装置刚度的增大而增大;墩顶位移在0＜η＜0.2的范围内呈递减趋势，当刚度比η＞0.2后，墩顶位移波动下降;对于Ⅳ类场地(软土场)，当η＞0.2之后，波动性较明显，但是η在0.1～0.2范围内取值时，基底剪力和墩顶位移两项指标能取得较低的响应。从上述二图中可得出，除Ⅳ类场地外，总体来看场地类型对合理刚度取值的影响并不明显。当设防烈度为8度罕遇地震时，梁间连接装置的合理刚度可取为0.05～0.15倍的梁体线刚度，此时墩顶位移和基底剪力两个指标能较好地平衡。

3.3 不同设防烈度下连梁装置刚度取值研究

5.12 汶川地震中，获得了大量的长持时强震记录。为了研究设防烈度对连梁装置刚度的影响，这里选用了Ⅱ类场地的4条汶川地震动典型强震记录(如表2所示)，并计算了4条记录下不同设防烈度所对应的均值需求谱曲线，如图11所示。

图9 不同场地下墩顶位移与刚度比间关系Fig.9 Displacement at the top of the pier vs stiffness ratio under different site soils

图10 不同场地下基底剪力与刚度比间关系Fig.10 Shear force at the bottom of the pier vs stiffness ratio under different site soils

表2 所采用的汶川地震动记录Tab.2 Ground motion records selected from Wenchuan Earthquake

图11 汶川地震动的均值需求谱曲线Fig.11 Mean demand spectra curves for records of Wenchuan Earthquake

按照性能点轨迹法，对于三种设防烈度(PGA=0.2 g、0.4 g、0.6 g)分别求解设定地震动水平下桥梁的性能点。图12和图13分别给出了三种烈度下连接装置刚度对桥梁结构的墩顶位移和基底剪力的影响规律。

当PGA为0.2 g时，在加设连梁装置后，结构的墩顶位移有所下降，但其基底剪力也相应有小幅度增大;随着连梁拉杆刚度的进一步增大，桥梁结构的基底剪力和墩顶位移基本上保持不变。因此，当PGA不超过0.2 g时，连梁装置对铁路简支梁桥地震响应的影响并不大，在此种设防烈度水平下无须加设连梁装置。

当PGA为0.4 g时，较小的刚度(η在0～0.15范围取值)对墩顶位移和基底剪力的影响显著:墩顶位移随着刚度的增大明显减小，基底剪力则随着刚度的增大而有所增大。但是，当刚度比η超过0.15后，刚度的变化对结构地震响应的影响明显降低。结合图中两项指标的分布规律，当设防烈度PGA=0.4 g时，连梁装置的刚度比η可在0.1左右取值。

当PGA为0.6 g时，较小的刚度(η在0～0.1范围取值)对墩顶位移和基底剪力的影响较大:墩顶位移随着刚度的增大明显减小，基底剪力则随着刚度的增大而明显增大。但是，当刚度比η超过0.2后，刚度的变化对结构的弹塑性地震响应影响微小，连梁装置的刚度可取为梁体线刚度的0.2倍。

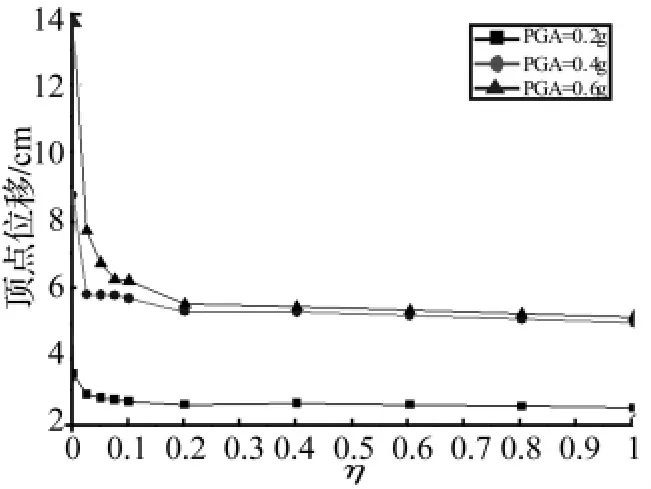
图12 不同设防烈度下墩顶位移与刚度比间关系Fig.12 Displacement at the top of the pier vs stiffness ratio for different fortification intensities

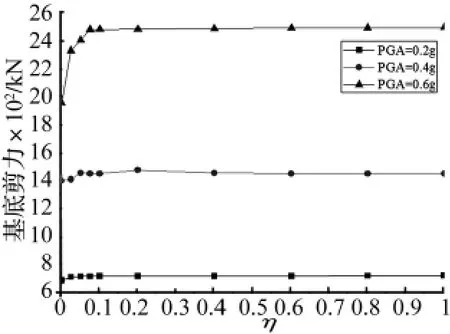
图13 不同设防烈度下基底剪力与刚度比间关系Fig.13 Shear force at the bottom of the pier vs stiffness ratio for different fortification intensities

4 基于非线性动力方法的连梁装置刚度检验

为了验证上述结论，引入表2中的两条汶川地震记录(51MZQ(EW)、51SFB(EW))，调整峰值加速度PGA为0.4 g，对全桥模型分别进行非线性动力时程计算，对比讨论设置不同刚度的连梁装置后桥梁各项指标的分布规律。

图14和图15给出了上述两条记录下桥梁各部位变形、剪力、弯矩等指标随连梁拉杆装置刚度的分布特征。在两条记录激励下，各项指标的具体取值尽管存在差异，但其分布随拉杆刚度的变化趋势基本一致。从图14中可看出，在小刚度比范围内，拉杆装置对梁、梁(台)相对位移以及墩顶位移有显著的抑制作用，但当刚度比η超过0.2时，上述指标随拉杆刚度的变化不明显。从图15中可看出，墩底剪力、弯矩随拉杆刚度的增大在小刚度范围内有所增大，但刚度进一步增大之后没有显著递增。综合上述两类指标，对于所选用的两条Ⅱ类场地的地震记录，其合理的连梁拉杆装置刚度在0.1～0.15倍的梁体线刚度范围内取值，此时变形、剪力二指标能取得较好的平衡，连梁装置能较好地发挥作用，这一结论和第3节基于非线性静力方法的研究结果一致。

图14 梁端相对位移及墩顶位移随连梁装置刚度变化关系Fig.14 Relative displacement between beams and deflection at the top of piers vs stiffness of the unseating prevention device

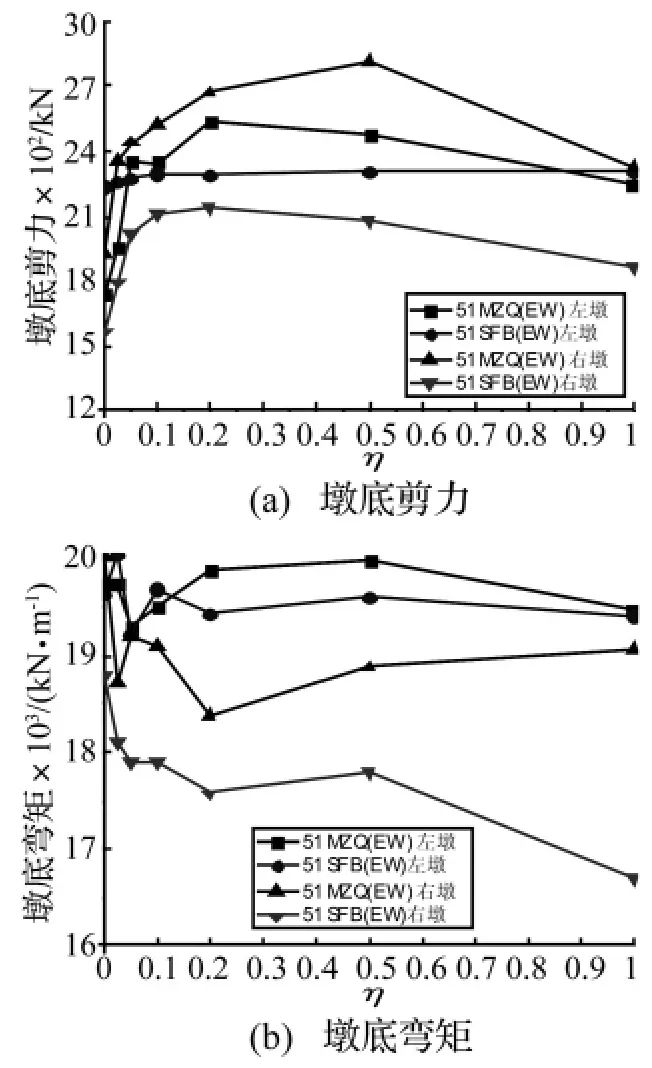
图15 左、右墩墩底剪力与弯矩随连梁刚度变化图Fig.15 Shear force and bending moment at the bottom of piers vs stiffness of the unseating prevention device

5 结论

本文采用能力谱方法和非线性动力时程方法，对墩高为20 m的(16+24+16)m铁路RC简支梁桥进行了纵向连梁装置的刚度参数优化分析，可得到如下结论:

(1)连梁拉杆装置是防止纵向落梁的一种有效措施，连梁拉杆的合理刚度取值对桥梁的整体抗震性能具有显著影响。

(2)对于Ⅰ、Ⅱ、Ⅲ、Ⅳ等四类场地，除Ⅳ类场地存在波动之外，总体来看场地类型对合理刚度的取值无明显影响，在8度罕遇烈度下，连梁装置的刚度可取为0.05～0.15倍的梁体线刚度，此时可有效抑制桥梁的地震响应，取得较为明显的抗震效果。

(3)桥址设防烈度对连梁装置的合理刚度取值影响显著。当PGA不超过0.2时，加设连梁装置没有明显的效果，可不予设置;当PGA为0.4 g和0.6 g时，连梁装置对桥梁地震响应有显著的影响，此时的合理刚度分别为梁体线刚度的0.1和0.2倍。

需说明的是，本文的研究是从数值分析角度出发，假定连梁拉杆满足强震下的强度需求，探讨不同场地和设防烈度下梁式桥连梁装置合理刚度的取值，存在一定的理想化。在实际工程中，限于施工和安装条件，当刚度比η超过0.15后，所需刚度一般较难实现，可通过其他方式如设置耗能阻尼器等加以弥补。

［1］叶爱君.桥梁抗震［M］.北京:人民交通出版社，2002.

［2］Saidi M，Maragakis E，Feng S.Parameters in bridge restrainer design forseismic retrofit［J］.JournalofStructural Engineering，1996，122(1):61 －68.

［3］Priestley M J N，Seible F，Calvi G M.Seismic design and retrofit of bridges［M］.New York:Wiley，1996.

［4］American association of state highway and transportation officials. Standard Specifications forHighway Bridges，Division I－ A Seismic design［S］.16th edition，1996.

［5］Desroches R，Fenves G L.Design of seismic cable hinger estrainers for bridges［J］.Journal of Structural Engineering，2000，126(4):500 －509.

［6］朱 晞，王根会，李宏年.铁路简支梁桥纵向连续加固方案研究［J］.工程力学(增刊)，1997.

［7］朱文正，刘健新.公路桥梁连梁装置研究［J］.公路交通科技，2009，26(4):68 －72.

［8］朱文正.公路桥梁减、抗震防落梁系统研究［D］.西安:长安大学，2004.

［9］王军文，李建中，范立础.桥梁中抗震限位装置设计方法的研究［J］.土木工程学报，2006，39(11):90－95.

［10］王军文，李建中，范立础.限位装置对连续梁桥地震反应的影响［J］.铁道学报，2008，30(3):71－77.

［11］中华人民共和国住房和城乡建设部.《铁路工程抗震设计规范》(50111－2006)(2009年版)［S］.2009，中国计划出版社.

［12］中华人民共和国交通运输部.《公路桥梁抗震设计细则》(JTG/T B02－01－2008)［S］.2008，人民交通出版社.

［13］Zhu P，Abe M，Fujin Y.Evaluation ofpounding countermeasures and serviceability of elevated bridges during seismic excitation using 3D modeling［J］.Earthquake Engineering and Structural Dynamics，2004，33:591 －609.

［14］Zhu P，Abe M，Fujin Y.Modelling three-dimensional nonlinear seismic performance of elevated bridges with emphasis on pounding of girders［J］.Earthquake Engineering and Structural Dynamics，2002，31:1891 －1913.

［15］FEMA440.Improvement of nonlinear static seismic analysis procedures［R］.Federal Emergency Management Agency，Washington D.C，2005.

［16］Applied Technology Council(ATC).Seismic evaluation and retrofit of concrete building report ATC －40［R］.Redwood City，USA:Applied Technology Council，1996.