带有期望补偿的自适应鲁棒控制律设计及比较分析✴
2012-06-02陶瑞超杨亚非
陶瑞超,杨亚非
(哈尔滨工业大学控制与仿真中心,黑龙江哈尔滨 150080)
随着计算机技术的不断发展,国内外学者对伺服系统控制算法进行了大量的研究,使得伺服系统的控制性能得到了很大的提高.传统的控制算法PID控制适用于可建立精确数学模型的确定性系统,通过对误差输入信号进行比例、积分、微分运算合成控制输出[1],由于其结构简单易于实现,成为应用范围最为广泛、应用时间最长的控制算法,但是对含有不确定性的非线性系统难以进行有效控制.自适应鲁棒控制[2-4]既具有自适应控制的学习能力和高精度的稳态输出,又具有鲁棒控制对于未建模动态和扰动的鲁棒性以及优越的暂态性能,能够满足伺服系统高精度的跟踪要求.传统的自适应鲁棒控制回归量在模型补偿中和参数自适应律中都是直接根据状态变量计算的,其自适应环节的性能在实际应用中可能会受到测量噪声的影响.本文以传统自适应鲁棒控制为基础,给出了带有期望补偿的自适应鲁棒控制方法,并对控制性能进行比较分析.
1 建立被控对象模型
伺服系统的执行机构为电机,在电机模型的推导过程中,由于电气响应很快,电流的动态特性与机械的动态特性相比是可以忽略的.电机的数学模型表达为[5]

式中:Y代表惯性负载的位置;M为惯性负载的转动惯量;u为电机的输入电压;F为所有不确定非线性如摩擦力矩Ff,波动力矩Fr和外部扰动Fd的总和.根据对多种经典摩擦模型的分析,简便并且恰当的方法是认为摩擦力矩是速度的静态非线性函数,设为Ff(﹒y),其形式为

式中:B是系统的等价粘滞摩擦系数;Ffn是非线性摩擦项,其模型为[6]
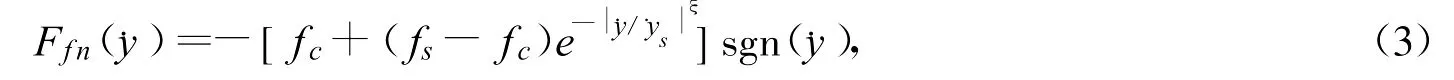
式中:fs是最大静摩擦值;fc是最小库伦摩擦值;﹒ys和ξ是用来描述 Stribeck效应的经验参数.由于系统中其他组成部分造成的误差,摩擦力矩还与角位置y有关,将这部分摩擦力矩归于外部扰动Fd.
由摩擦模型的函数式(3)可知,该模型在速度为零时是不连续的,因此不能采用该模型作为摩擦补偿的模型,因为电机无法输出不连续的力矩.为避免上述问题,利用一个简单连续的摩擦模型来近似实际的不连续摩擦模型,选取摩擦模型的近似模型为

式中:Af未知;Sf(x2)为连续函数,将近似摩擦模型的误差归为系统的总扰动d,d=¯Ffn-Ffn+Fd.
将摩擦模型的近似模型式(4)代入电机模型式(1),得到被控对象模型为

式中:x=[x1,x2]T代表被控对象的位置和速度的状态向量;y是位置输出,=d-dn,dn代表系统总扰动力矩d的标称值.
取xd(t)为期望输出轨迹,跟踪误差表示为z=x-xd(t),控制的目的是设计有界的控制律u使跟踪误差z(t)尽可能小.
2 带有期望补偿的自适应鲁棒控制


定义期望回归量 φd(t)=φ(xd(t)),回归量误差 ~φ=φ(x)-φd,用期望回归量 φd(t)替代被控对象模型式(6)中的 φ(t).选取自适应律形式为[7]


性质1:该映射具有如下性质
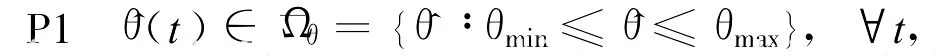
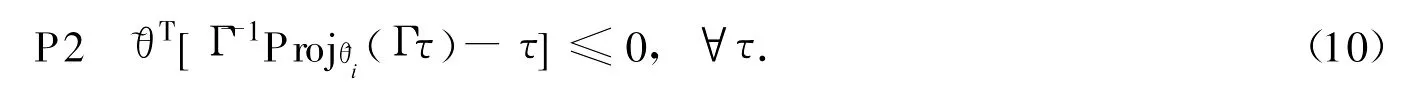
因此,带有期望补偿的自适应鲁棒控制控制律表示为
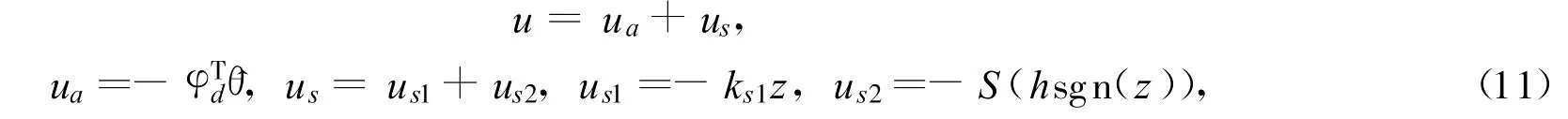
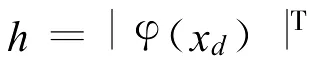

综上,将期望补偿自适应鲁棒控制律式(11)代入系统模型式(6)中可得

由中值定理可得

式中:gf(x2,t)是确定的_非线性函数.设计ks1为足够大的正数,使得矩阵

是正定的.由式(13)可以得出,如果要使矩阵A≥0,则当且仅当ks1满足
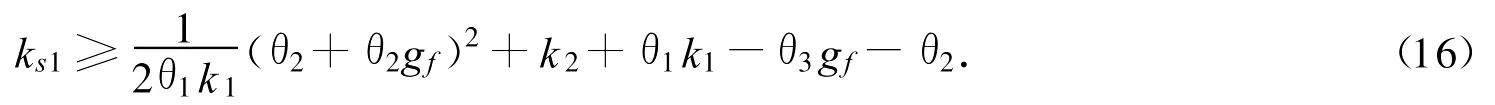
结论:若采用带有期望补偿的自适应鲁棒控制律式(12)和基于非光滑投影的参数自适应律式(8),则:①当系统存在非线性不确定性时,系统输出渐进趋近于常数;②若系统只存在参数不确定性,稳态跟踪误差为零,并且当满足持续激励条件时,参数估计值趋近于它们的真值,并且由于期望补偿自适应鲁棒控制的自适应函数关于反馈信号是线性的(与z有关),该积分型自适应律可以使参数估计^θ和模型补偿ua都对于测量噪音不敏感.
选取期望轨迹为正弦曲线xd=sint,采用期望自适应鲁棒控制律进行补偿,得到仿真结果如图1.

图1 带有期望补偿的自适应鲁棒控制跟踪误差曲线Fig.1 Tracking error of DCARC control law
由仿真曲线可以看到:带有期望补偿的自适应鲁棒控制的跟踪误差趋近于一个非常小的常数,并且跟踪性能的动态响应快速.
3 控制性能对比
采用PID控制反馈补偿时,被控对象模型式(1)改写成

在对象模型中,利用已知的变量y(t),﹒y(t),yd(t),﹒yd(t),¨yd(t)设计系统控制输入为

将式(16)代入式(1)中可以得到系统闭环特征方程为
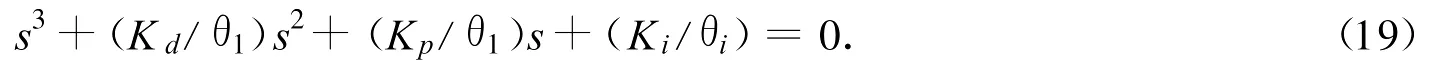
通过闭环函数极点配置可以计算出Kp,Ki,Kd的值.在仿真验证时,由于参数 θ1,θ2,θ3是未知的,所以初始估计值(0),(0),(0)代替为

同样选取期望轨迹为正弦曲线xd=sint,采用期望自适应鲁棒控制律进行补偿,得到的仿真结果如图2所示.

图2 PID控制跟踪误差曲线Fig.2 Tracking error of PID control law
由图2可以看到:系统误差存在衰减振荡过程,并且最终的输出误差存在一定稳态误差.带有期望补偿的自适应鲁棒控制性能与PID控制相比,跟踪误差更小,并且具有良好的参数估计效果.
4 结 论
本文采用带有期望补偿自适应鲁棒控制方法实现对伺服系统的控制,通过采用Matlab/Simulink进行仿真验证.由仿真得到的跟踪误差曲线可见,带有期望补偿的自适应鲁棒控制方法能够满足高精度跟踪的性能要求.与传统PID控制进行对比,通过仿真结果可以看到:带有期望补偿的自适应鲁棒控制性能可以得到更高精度的伺服跟踪效果.
[1]Hua Sun,Dai Yuehong.Fuzzy PID control and simulation experiment on Permanent Magnet Linear Synchronous Motors[C].Proceedings of International Conference on Electrical and Control Engineering,2010:1047-1049.
[2]Krstic M,Kokotovic P.Adaptive nonlinear design with controller-identifier separation and swapping[J].IEEE Trans Automatic control,1995,40(3):426-440.
[3]Li Xu,Bin Yao.Adaptive robust precision motion control of linear motors with negligible electrical dynamics:theory and experiments[J].IEEE/ASME Transactions on Mechatronics,2001,6(4):444-452.
[4]Bin Yao,M Tomizuka.Adaptive robust control of M IMO nonlinear systemsin semi-strict feedback forms[J].Automatica,2001,37(9):1305-1321.
[5]杜坤梅,李铁才.电机控制技术[M].第2版.哈尔滨:哈尔滨工业大学出版社,2002:1-6.
[6]王英,熊振华,丁汉.基于状态观测的自适应摩擦力补偿的高精度控制[J].自然科学进展,2005,15(9):1100-1105.
Wang Ying,Xiong Zhenhua,Ding Han.High-precision control of adaptive friction compensation based on state observer[J].Progress in Natural Science,2005,15(9):1100-1105.
[7]Yao Bin,Tomizuka M.Smooth robust adaptive sliding mode control of robot of Dynamic Systems[J].Measurement and Control,1996,118(4):765-770.
