城市交巡警平台的设置与调度优化模型

2012-06-02张成堂

重庆理工大学学报(自然科学) 2012年11期

张成堂

(安徽农业大学理学院，合肥 230036)

2010年2月8日，一支名为“交巡警”的全新警种在重庆正式诞生。城市交巡警平台的设立保证了在事故发生时交巡警能尽快赶到事发现场，提高了工作效率，减少了社会上不安全事件的发生，从而有效保证了公民的生命财产安全。然而，由于警务资源是有限的，怎样在警力有限的情况下，根据城市的实际情况与需求合理地设置交巡警服务平台以及分配各平台的管辖范围，以保证在事件发生后合理调度警务资源，使得能在最短时间内有警力到达事件现场，是警务部门研究人员在城市道路交通事件应急管理中所面临的一个重要课题。目前，中国的应急警力设置与调度基本都是依靠个人经验，缺乏理论科学依据，本文将根据模型给出城市交通网络中交巡警服务平台的管辖范围(问题1)，并解决当出现突发事件时，如何合理调度警力以达到快速响应目的的问题(问题 2)［1－10］。

1 基本假设与符号约定

从所给的某市主城区(A区)的交通网络与平台设置的示意图以及全市6区交通网络与平台设置的示意图来看，实际情况非常复杂，为了便于分析，假设:①不考虑城市交通各种因素影响，假定交巡警出警时的平均车速为60 km/h;② 每次交巡警接案后，都以最短路径到达出事地块边缘，即为到达出事地点，现场处理案件所用时间相同;③图1、2中，假设城市交通网络中相通的各节点邻接线为直线，道路均可双向通行;④警方实施围堵时，逃犯出逃方向随机，但只能通过出入城区通道逃逸，并且逃犯驾车逃跑的平均车速与警车速度相当。

有关符号约定:v表示警车的行驶速度;lj表示 A 区第 j个路口节点(j=1，2，…，582);dij表示标号为i的路口到标号为j的路口的最短距离(i、j=1，2，…，582);Ai表示A 区第i个交巡警平台编号(i=1，2，…，20);Bi表示 B区第 i个交巡警平台编号(i=1，2，…，8);Ci表示C区第 i个交巡警平台编号(i=1，2，…，17);Di表示 D 区第 i个交巡警平台编号(i=1，2，…，9);Ei表示E区第i个交巡警平台编号(i=1，2，…，15);Fi表示F区第i个交巡警平台编号(i=1，2，…，20);t为出警所用的最长时间;wij为相邻2个节点之间的距离，即权值(i、j=1，2，…，582);r为平台警力在 t内能走过的最大路程;αj为各节点的发案率;mi为衡量警务平台工作量大小的综合指标;ρi为各城区的人口密度(i=1，2，…，6);ni为各城区的人口数(i=1，2，…，6);si为各城区的面积(i=1，2，…，6);ψi为各城区的合理性指标(i表示A，B，…，F等城区)。

2 模型分析

2.1 问题1的模型分析

对于如何分配A区交巡警服务平台的管辖区域，首先考虑以各服务台为圆心，以t内警车所走过的最大路程为半径来做圆(图1)，其中半径即为 r。由 r=vt，令 t=3 min，v=60 km/h，可得r=3×103m，由比例尺可知图1上半径为30 mm。从图1中可以直观地分析出哪些服务台一定可以管辖哪些范围，确定出点l23应属于A13管辖。然后利用Matlab计算出各个路口节点的距离并找出各坐标所对应的路口节点，根据Dijkstra算法得出每个路口节点到其他任意节点的最短距离，最后编制Matlab程序的矩阵算法将上述矩阵提取子矩阵，可算出每个交巡警服务平台所对应的较短的路口节点，从而给出了警务平台管辖的范围。

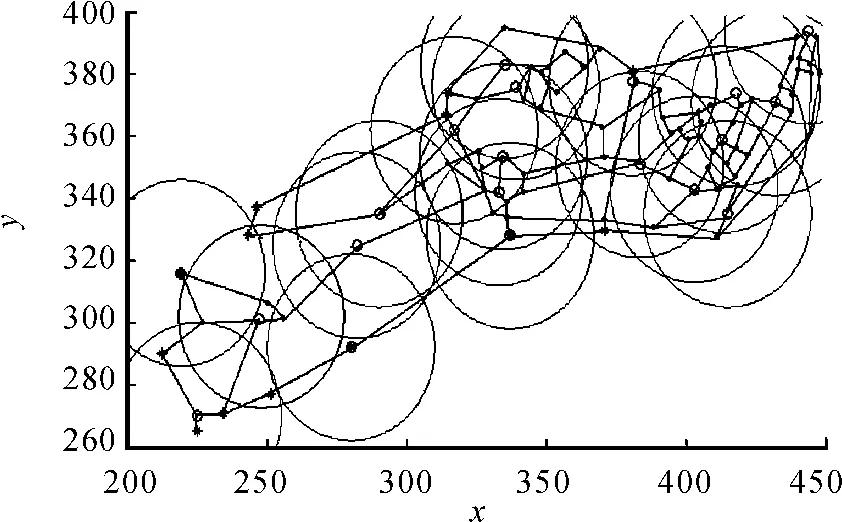
图1 某市A区的交通网络与平台设置的示意图

对于如何调度20个服务平台警力封锁13个出入口，拟采取分区域距离算法先排除7个服务平台，然后利用整数规划将13个服务平台分配到13个出入口，使得所有交巡警行驶的总距离最短，从而可以指派警力执行全面快速的封锁任务。

对于如何添加警务平台的问题，主要从交巡警服务平台的工作量不均衡，以及有些平台出警时间过长等情况出发，来确定新增服务平台的位置。为此，先由综合指标即通过交巡警服务平台至各节点的最短距离与相应节点的发案率的乘积之和来衡量各个警务平台的工作量大小，再考虑出警时间超出3 min的节点，综合以上因素即可确定新增服务平台位于哪个已有警务平台所管辖的区域内，再确定其具体位置和数量。

2.2 问题2的模型分析

对于全市警力配置的合理性研究，首先要判断该市现有交巡警服务平台设置的方案合理与否。可从各城区的总发案率、城区的节点总数、城区面积、人口数以及人口密度5个方面予以考虑。根据交巡警服务平台的设置原则，由于5个因素标准不统一，考虑利用主成分分析将5个指标归一化，以此衡量该市交巡警服务平台设置的合理性，结论为该市当前的警力配置不合理。根据问题1已求出的管辖范围和工作量，结合现有的交通网络与平台配置，即可得到一个合理的解决方案。

对于如何调度全市警力围捕逃犯的问题，由于逃犯的出逃速度未知，通过分析全市警务平台配置(图2)，进而确定可能出现的2种情形和相应预案:① 逃犯速度小于71.82 km/h，逃犯未能进入C区。若逃犯在A区或A、C两区之间，则此时需要堵住C区的236和237号入口节点，以及A区除30、38号以外的路口(分配方案同问题1)，而路口236和237 则由 C6、C8、A5、A8中的2 个距离出口最近的交巡警平台负责封堵，最终得到围堵方案1;② 逃犯速度大于71.82 km/h，逃犯已能进入C区(假设从最近的30号或48号路口逃脱)。若逃犯已从A区逃脱，且有可能进入C区，则此时需对全市进行围堵。根据全市交通网络与平台设置的示意图，首先可大致确定151、153号路口由B4、B5、B7负责，177、202 号路口由 C10、C12负责，203号路口由C13负责，317由C16负责，264由C1、C2负责，325由 D6负责，362由 D3、D4负责，328由D9负责，332由E15负责，387由B8负责，418由E5负责，483由 F9负责，541由 F10负责，572由F11负责，578由F5负责。其余未能确定封堵的节点，可依据交巡警到达其节点所用时间最短来进行指派，由此可得围堵方案2。

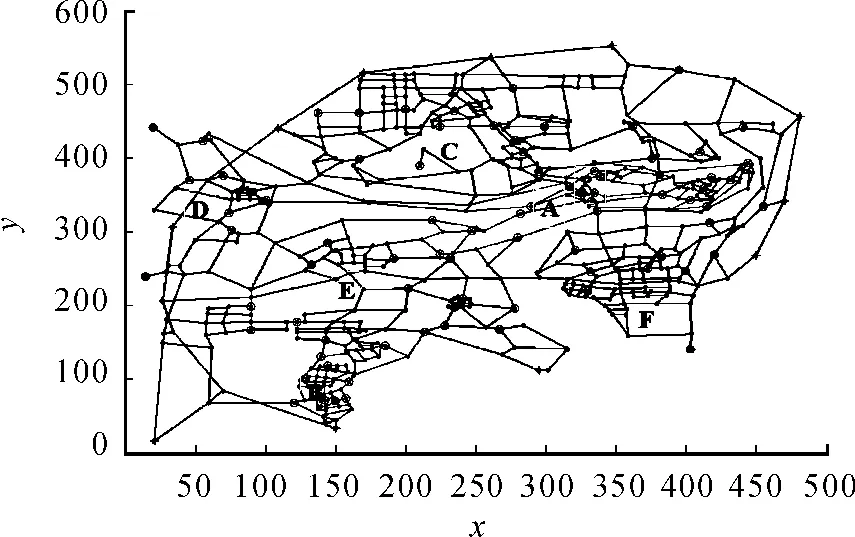
图2 某市6区交通网络与平台设置的示意图

3 模型的建立与求解

给定图 G=(V，E)，对 G中的每一条边(li，lj)，相应的有一个数 wij，称这样的图为赋权图，其中 wij称为边(li，lj)上的权。

Dijkstra算法不仅可以找到任意两点之间的距离，还可以给出从任一个点出发到赋权图中所有顶点的最短路径。

由于Dijkstra算法时间复杂度高，效率较低，本文采用Dijkstra矩阵算法，其步骤为:

步骤1 输入加权图，存储于矩阵A=(aij)n×n中，其中n为图G的顶点个数，

步骤2 求出顶点lk到其他各顶点的最短距离，并保存在矩阵A的第k行(k=1，2，…，n)中，算法结束后矩阵A的元素值即为任意两个顶点间的最短距离。

3.1 基于最短路径的管辖区域分配

警车行驶速度是60 km/h，要求尽量不超过3 min到达事故现场，也就是说行驶的距离尽量不超过 3 000 m，对应到图1上的比例尺应该是30 mm。为了使A区交巡警在案发后最快到达所辖范围的路口，首先应分别计算出路口节点到20个警务平台的路径长度，从中选出最短路径，将该节点划分到最短路径对应的平台管辖范围。可设标号为 i的路口节点坐标为(xi，yj)，i，j=1，2，…，92，则相邻路口节点间距离为

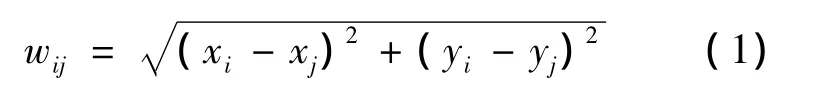
根据上述距离公式，利用Matlab软件包可得每个节点对应路径最短的警务平台编号，从而将节点初步划分到对应平台，例如节点l23应属于A13管辖。对于部分节点到2个或以上警务平台路径相等，或到平台的空间距离很近但实际路径很长等情形，进一步考虑通过Dijksra算法先求出各个节点到其他各节点的最短距离，找出20个警务平台在3 min内能到达的最近节点，并结合每个警务平台工作量的饱满程度进行适当调整，即可给出A区交巡警服务平台所管辖区域(见表1)。

表1 A区的交巡警服务平台所管辖区域

3.2 封锁A区的警力调度方案

如果A区出现重大突发事件，现在要调度全区20个交巡警服务平台的警力资源，对该区13条条交通要道实现快速全面封锁。鉴于警力资源有限，出入A区的交通要道只考虑由1个交巡警服务平台负责。首先，进行13个交巡警服务平台的选择。由图1中13个交通要道的分布位置来看，若要实现最快全封锁，应将平台 1、3、17、18、19、20排除，再依据任意2个路口节点的最短距离及20个平台的管辖范围，可以将平台6排除。剩下的13个服务平台对应13个出入路口，可以利用指派问题进行警力调度。

引入变量 xij(i=1，2，…，20;j=12、14、16、21、22、23、24、28、29、30、38、48、62)，并令

根据题意和前述假设，建立如下指派问题:

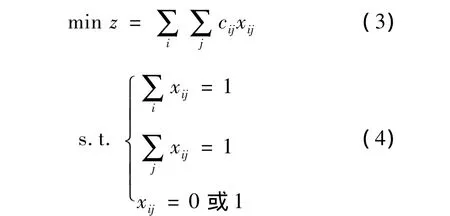
其中 cij＞0(i=1…20;j=12、14、16、21、22、23、24、28、29、30、38、48、62)表示指派第 i个警务平台去封锁第j个路口节点所走的路程。式(3)表示第j个路口只能由一个平台封锁。式(4)表示第i个警务平台只能进行一项封锁任务。利用匈牙利算法对此指派问题进行求解，可确定出具体调度方案(见表2)。此时，每个警务平台封锁A区所走路程最短为8 017 m，即最短耗时为8.017 min。

表2 封锁A区13个出入口的警务平台调度方案

3.3 A区警务平台的增设方案

通过表1可直观地发现警务平台的工作量大小不均衡，而有些地方有出警时间过长等实际情况。利用工作量指标计算可得，平台A2、A5、A7、A15、A20工作量相对较大，其 m 值均超过90。有6个节点出警时间过长，超过3 min，其节点标号是 l39、l61、l28、l29、l38、l92，分别属于 A2、A7、A15、A16、A20警务平台管辖。

在上述需要调整的 A2、A5、A7、A15、A16、A20六个服务平台中，A2和A16所负责的l38、l39号节点出警时间过长，但由于这2个节点距离较近，故综合考虑A2和A16两个服务平台的范围，这样只增加1个新的服务平台就可以解决2个节点出警时间过长的问题，因此，就考虑在 A5、A2(A16)、A7、A15、A20所负责的节点范围内增加新的交巡警服务平台。

对于A5所负责的8个节点(自身所在节点除外)，采用改进的Dijkstra算法，计算任意一个节点到其他7个节点的最小m值之和，可得节点l50与其他7个节点的m值之和最小，由此可以确定，应在节点l50处增加新的交巡警服务平台。同理依次讨论节点 A2(A16)、A7、A15、A20，依据其工作量指标(表3)，相应的警务平台应增设在节点 l40、l48、l28、l90处，加上前面的节点l50，总共增加了5个警务平台。

3.4 全市警务平台的合理调节

人口密度=地区人数/地区面积，城区总发案率=城区内各节点发案率之和，即

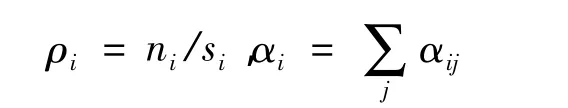
从而得到全市6个城区数据统计结果，见表4。

以6个城区的面积 x1、人口 x2、节点数 x3、总发案率x4和人口密度x5为样本，进行主成分分析。使用Matlab软件编制程序，可得相关系数矩阵R为

其特征值 λ =0.002 4，0.019 9，1.137 6，1.828 5，2.011 6。

主分量Zk的贡献率为，主分量 Z1，…，Zm(m＜p)的累计贡献率为，由此可得x5的贡献率为类似运算可知 x4的贡献率为36.57%，x3的贡献率为22.752%，x5和x4的累计贡献率为76.802%，小于80%，又x5、x4和x3的累计贡献率为99.554%，故选取x3、x4、x5作为主分量。由此可选

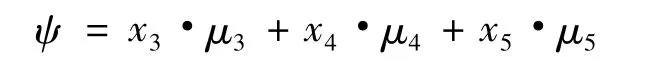
为合理性指标，代入样本数据计算可得6个城区的合理性指标分别为

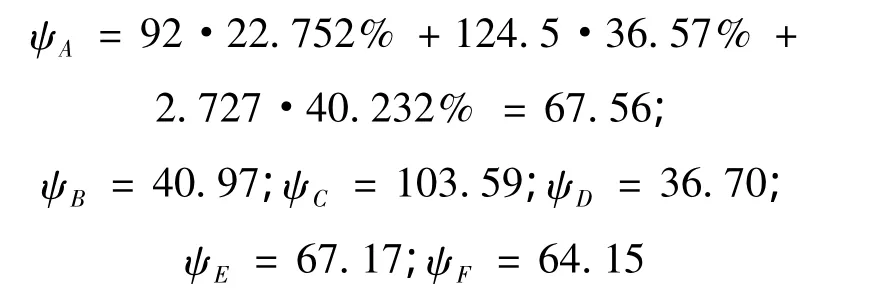
即C城区应分配最多的交巡警服务平台，A城区次之，E城区第3，F城区第4，B城区第5，D城区最少。

结合该市现有的交巡警服务平台配置方案，可知现有方案明显不合理，A城区应减少警务平台数量，C城区和D城区应增加警务平台。具体调节方案如下:

1)根据问题1算出的A城区各交巡警服务平台的工作量，可知A19工作量最小，可移除;

2)由于C城区应增加服务平台，根据问题1中采用的算法，可以确定在315号节点和206号节点处各增加1个警务平台比较合理;

3)另外由全市6区交通网络与平台设置的示意图(图2)可以看出387号出口与其最近的服务平台距离过大，又考虑到D区应增加警务平台，因此确定在329号节点处增加1个警务平台。

表3 各警务平台的工作量指标(m值)

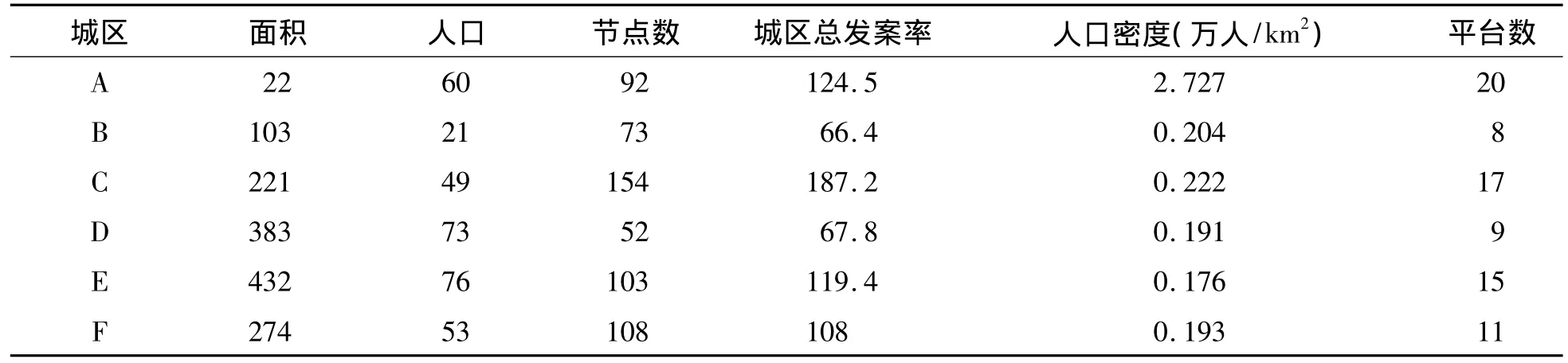
表4 六城区的数据统计结果

3.5 最佳围堵方案

逃犯逃离A区的最短路径是从p点驾车向出口节点30行驶，再通过节点237进入C区，而p点到节点237的最短路径的图上距离为35.91 mm，故由此可求得逃犯逃出 A区的临界速度为71.82 km/h。

由于逃犯的驾车出逃速度未知，在报警后，逃犯所在区域有2种可能:① 当逃犯速度小于71.82 km/h时，逃犯未能进入C区;② 当速度大于71.82 km/h时，逃犯已能进入C区(假设从最近的30号或48号路口逃脱)。鉴于此，应考虑以下2种预备方案:

方案1 考虑到逃犯的逃跑方向及2个出口到其余平台的距离，将路口l236分配给交巡警服务平台C6负责，路口l237分配给C8负责，由此得到围堵方案1(见表5)。

方案2 根据Dijkstra矩阵算法可求得任意2点间的最短距离，结合指派问题可知，对于l151出口，距其最近的服务平台为B4，最短图上距离为31.94 mm，对于l153出口，距其最近的节点为B7，最短图上距离为44.70 mm，故由此将l151路口分配给B4负责，l153路口分配给B7负责。同理，可求出其余未定的路口，最终得到围堵方案2(见表6)。

表5 封锁市区出入口的警务平台调度方案1

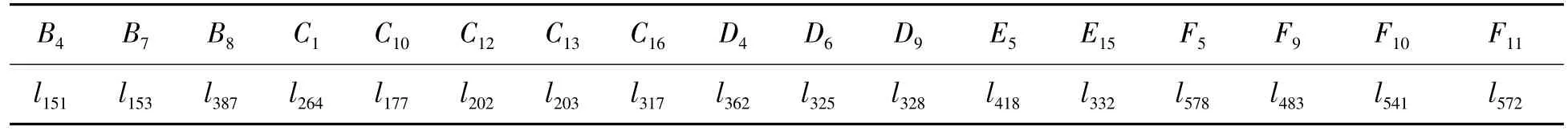
表6 封锁市区出入口的警务平台调度方案2

4 方案改进

该模型主要根据已有交通数据和图形作预处理的筛选，然后采用Matlab软件结合Dijkstra算法得到A城区警务平台的合理管辖范围，并由警务平台工作量的指标权值衡量出应该增加的平台数，建立了突发事件时警力调度的指派问题，通过匈牙利算法最后确定出A城区警力的最优调度方案。对已有结果和市区相关数据信息进行统计分析，评估该市市区现有平台设置的合理之处和改进方案。

该模型还是有一定的局限性，因为一般情况下道路不会畅通无阻，即不可能保证出警时间都在3 min之内，此外，警车速度不可能与逃犯驾车逃跑速度完全一致，因此对于A区发生的案件，考虑到以上诸多实际因素，可以将指派问题进行改进(表7)。数据检验表明，改进方案后，最后一个到达封锁点的是警务平台A10到节点l12处，行驶路程缩短至6 364 m。

因此，对于全市性的封堵方案类似可作上述改进。本模型合理调节了警务平台的设置，优化了调度方案，当有事故发生时，交巡警可以快速地到达事故现场，提高了工作效率，从而有力地保证了公民的生命和财产安全。同时该模型还可以拓展应用到其它资源配置优化模型中去，如公用电话亭的配置、防空洞的配置、消防救援工作的最短路径选择问题等。