改进遗传算法在线阵波束方向图中的应用
2012-06-01湖南工学院电气与信息工程系伍麟珺
湖南工学院电气与信息工程系 伍麟珺
改进遗传算法在线阵波束方向图中的应用
湖南工学院电气与信息工程系 伍麟珺
通过对传统遗传算法应用在线阵波束方向图中进行分析,从编码方式、变异策略以及选择机制上提出了新的改进策略。改进后的算法减少了编码长度,增加了变异灵活性,更好的保持了种群中个体的多样性,加快了搜索和运算速度和收敛性能。对线阵波束方向图的零陷点生成和旁瓣抑制进行仿真,仿真结果表明改进算法与传统算法相比能明显减少遗传代数,能够更快地找到满意解。
智能天线;波束形成;遗传算法
1.引言
上世纪八十年代以来,移动通信技术在全球范围内得到迅速发展。移动通信用户和业务的不断增加,使得无线资源日趋紧张。再加上现代工业的污染和气候变化,通信环境变差。在复杂的移动通信环境和频带资源受限的条件下,如何达到更好的通信质量和更高的频谱利用率,成为移动通信研究中的热点问题。在这样的技术背景下,智能天线技术应运而生。智能天线技术其原理是将无线电的信号导向具体的方向,产生空间定向波束。使天线主波束对准用户信号的对准用户信号到达方向。旁瓣或零陷对准干扰信号到达方向,达到充分高效利用有用用户信号并抑制干扰信号的目的[1]。
遗传算法是模拟生物在自然环境中的遗传和进化的过程而形成的一种自适应全局优化概率搜索算法。1994年,J.Michael Johnson和Yahya Rahmat-Samii首次将基本遗传算法应用到天线综合中[2][3],提供了用遗传算法进行阵列综合的一般方法。此后智能算法被不断地应用到天线阵综合问题中。
2.基本遗传算法的改进策略
作为一种先进的新型智能算法,遗传算法也不是完美无缺的。该算法随机性强,依赖于大量的个体筛选,易出现早熟收敛等现象。[4][5]于是很多学者针对天线阵列的特点,提出了各自的改进策略。文献[6]采用浮点数编码替代传统的二进制编码,文献[5]将量子门操作融入到基本算法中,文献[7]针对遗传算法在天线图形成中的应用提出了合适的适应度函数。本文作者根据自身的学习体会,从编码方式,变异操作以及选择机制出发,提出了自己的改进策略。
2.1 整数编码
遗传算法中传统的编码方式有二进制编码和浮点数编码两种。二进制编码操作简单,当解精度要求较高时,采用该种方式会使得编码位数多,增加计算难度。浮点数编码适用于精度较高的场合,无需译码,提高运算效率,但无统一的适用于浮点数编码的遗传算法模式理论。
本文提出一种新型的编码方式,整数编码法。整数编码即每个基因的取值在一定的整数范围内,染色体由一串整数编码串表示。这种编码方式,对于实数形式的个体解尤为适合。每组编码的码长与其对应的实数解位数一致。按从高位到低位的顺序,实数解的每位数值,即是编码对应位基因的取值。如某个体解为5.230,则按照整数编码规则所得编码即为5230。编码位数仅为四位,与二进制编码相比大大缩短了编码长度,加快运算速度。
2.2 对10去补变1变异

图1 改进遗传算法流程图

图2 对称直线阵示意图
采用上述整数编码方式后,交叉操作可以按照二进制编码规则,但其取反变异操作明显不再适合。在本文采取对10取补和变1相结合的思路对变异操作进行改进。0到9十个整数都不超过10,且可以两两配对求和得10(5可以和它自身相加得10)。因此,在编码串中确定好待变异的基因座以后,用10减去待变异位置的基因数值,这样所得差值与原值至少相差2。可是一方面考虑到0和5这两个特殊的数值,对10取补法对它们计算后依然是原值。另一方面,如果某个基因座多次被选择进行变异,单纯对10取补会使该基因座的取值来回在一对数值之间变化,假设基因座i原值取3,进行对10取补后得7,如基因座i多次被选择变异,则其取值无法跳出3和7之外进行取值,这就失去了变异的意义。于是本文规定,在进行对10取补步骤后,再对所得值随机的加1或减1,这样就解决了上述两方面的问题。
2.3 跨代竞争
本文采用跨代竞争选择策略,所有父代个体均参与交叉和变异操作,这样就形成了父代,由交叉产生的子代(这里我们称为交叉子代)和由变异产生的子代(这里我们称为变异子代)三个种群,三个种群中的个体完全混合起来排列各自的个体适应度,然后按照一定的比例,从中选取最优的个体组成新的种群。这种选择策略打破传统遗传算法先选择再变化的顺序,而是首先让父代中所有个体均发生变化,然后再对整个大群体进行筛选。牺牲单纯的操作方式,既强调优良个体的保留,又保证父代中优秀个体也参与变化。
经改进后的遗传算法流程图如图1所示。算法以整数编码开始,首先产生第一轮种群,跟基本遗传算法不一样的是,改进遗传算法先对所有父代进行交叉变异操作。然后将父代种群,交叉子代种群和变异子代种群混合成大种群,统一计算适应度函数值,然后按照适应度高低排序,将大种群中适应度高的个体保存下来,适应度低的淘汰。形成新的一轮种群,再进行交叉变异操作,直至满足遗传终止条件,结束遗传算法运算。
3.对称线阵模型
天线阵列各个振子的可调参数主要包括激励电流的幅度和相位,为了研究方便,本设计做一些的简化。规定阵列天线单元之间的间距均为d,且电流激励的幅度矢量关于中心参考点呈对称分布。在实际的问题中调整天线的方向图的形状主要是依靠振子激励的幅度分量来实现的,本文只考虑振子电流激励的幅度,天线阵列参考模型如图2所示。
Ii为各阵元的电流激励值分量,根据直线阵列远场场强知识,图2所示简化的一维直线均匀阵列中,其归一化方向图函数为[8]:

4.实例分析
4.1 零陷位置控制
目前移动通信用户数量大增,在一定空间范围内不可避免的会有多个用户同时收发信号。则相互之间形成了干扰,在天线接收端,我们往往将增益较低的零陷方向对准主要干扰方向以期抑制干扰[9]。
假设由16个阵元组成的对称直线天线阵列,每个阵元间的间距均为λ/2,λ为入射波波长。通过调节阵元的激励电流幅值,改变天线图方向,使得在方向图在规定辐射方向的时候产生零陷。按文献[5]适应度函数为:


表1 16阵元直线阵零点生成仿真结果

表2 16阵元直线阵旁瓣抑制仿真结果
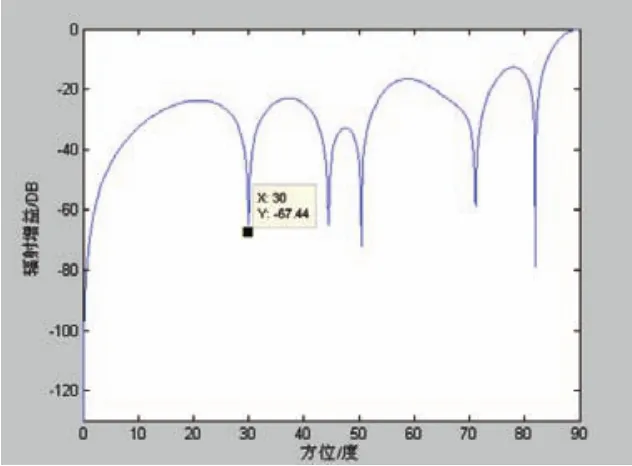
图4 基本遗传算法零陷位置控制

图5 改进算法零陷控制函数收敛图

图6 基本算法零陷控制函数收敛图
式(2)中n代表需要形成零点值的个数,在实际应用中对应的是需被抑制的干扰个数。bi为加权系数,其取值往往需要依靠经验多次尝试所得, 代表第i个干扰源的信号方向,NULLi是指第i个零点的零陷深度。本设计中n=1,Θ=30°,NULL取60db。16个阵元两两对称,则有8个待求解,即8个激励电流幅值分量。对幅值进行归一化处理,精度取至0.0001,则每个幅值对应的编码长度为4,共计32位编码。交叉概率取0.6,变异概率取0.4,初始种群规模取100,遗传代数取300。分别用改进遗传算法和基本遗传算法进行仿真,得到结果如表1所示。
从图3和图4可以看出两种算法均在30°处产生了零陷,但用改进零陷深度为-123.6db,而用传统遗传算法零陷深度为-67.44db。只要能使空间方向为30°处的辐射电平增益低于-60db的参数组合就认为对应解是合理的。从目标函数收敛图5和图6可见,改进遗传算法在200代以前得到满意结果,而传统遗传算法在250代以后才得到满意结果。
4.2 抑制旁瓣控制
抑制干扰的零陷点往往只有有限的几个,在较复杂的电磁通信环境中,这种方式不将干扰和噪声排除在外,如果其他方向尤其是靠近主瓣方向的旁瓣电平增益过高,可能在后续放大电路中淹没。所以一般将零陷点对准干扰信号最强的方向,然后将其他方向的电平抑制在一定的标准之下,拉开主旁瓣电平之间的差距,方便后续的滤波电路工作。
天线阵列形式按16阵元等间距一维直线对称阵,适应度函数采用文献[5]中的

SLLmax代表方向图最大旁瓣增益,Θm表示主瓣宽度,S代表旁瓣区域,SLLdes代表预设旁瓣电平最大增益。民用移动通信系统标准中,最高旁瓣电平不超过-18db[10]。本设计设定最高旁瓣电平不超过-20db。主瓣宽度10°,交叉概率0.7,变异概率0.3,初始种群规模100,遗传代数200代。仿真结果如表2所示。
图7所示为用改进遗传算法优化低旁瓣直线阵天线阵列方向图的最高旁瓣电平为-22.78db,实际主瓣宽度2*(±10.2°)。图8所示用传统遗传算法得到优化低旁瓣直线阵天线阵列方向图的最高旁瓣电平为-20.45db,实际主瓣宽度2*(±93°)。两个方向图在图形上存在较大差异,但都基本能满足设计要求。这进一步说明,满足求解条件的激励幅值组合存在多样性,因此单纯从数值上比较两组激励幅值是没有意义的。图9和图10是针对-20db的低旁瓣天线阵列设计,改进算法和传统算法目标函数收敛图。两图比较可知,改进算法在140代左右可以得到满意结果,而传统算法要在180代以后才能够得到满意结果,从目标函数收敛函数曲线的陡峭程度来说也是,改进算法的收敛曲线更为陡峭,这说明改进后的算法比传统算法收敛速度更快。

图7 改进遗传算法优化仿真旁瓣直线阵

图8 基本遗传算法优化抑制旁瓣直线阵

图9 改进算法抑制旁瓣收敛图

图10 基本算法抑制旁瓣收敛图
5.结论
本文通过对基本遗传算法的编码方式,变异操作以及选择机制进行改进,并将将改进后的遗传算法应用于无线波束方向图的优化。通过仿真结果对比发现,改进后的遗传算法在相等的参数设置下,比传统遗传算法收敛速度更快,能够在更短的时间内找到最佳解。
虽然得到的仿真结果很好的满足了方向图的要求,但是有一个非常严重的缺陷就是实时性的要求还有很大差距。在实际的应用中,用户可能是快速移动的,所以方向图也可能是要快速变化的,这时候对实时性的要求就非常高。所以这会是后续工作很重要的一部分。
[1]http://bake.baidu.com/view/150697.htm.
[2]Ozean.Mohanc.K.Partial shape matching using genetic algorithms.Pattern Recognition Letters,1997,18(1).
[3]Ren Q.S.,The Genetic searching algorithm for optimal length—limited codes with control.Journal of China Institute of Communications.1997,19(3).
[4]王小平,曹立明.遗传算法—理论、应用与软件实现.西安:西安交通大学出版社,2002,197-200.
[5]吴红海.混合遗传算法在智能天线赋形中的应用[D].北京:北京邮电大学,2007,37-38.
[6]范瑜,金荣洪.基于一种新的遗传算法的天线方向图综合技术.电波科学学报,2004(4)183-186.
[7]Kyoung Kim,Handbook of CDMA system design engineering and optimization.New Jersey:rentice Hall,2000.
[8]池越,张鹏垒.基于免疫克隆选择算法的天线方向图综合技术研究.通信技术,2009(5):1-73,134.
[9]殷洪沛,素珍.宽带相控阵天线的低副瓣设计.舰船电子对抗,2009(2):0-84.
[10]第三代移动通信系统TD-SCDMA智能天线阵列设备规范[S].动通信集团公司,2008,11-20.
The application about improved genetic algorithm in arraybeam pattern
WU Lin-jun
(Department of Information &Electric Engineering,Hunan Institute of Technology,Hengyang 421002)
Through analyze the traditional genetic algorithm applied on arraybeam pattern.The algorithm was improved in coding way,mutation strategy and choice mechanism.New algorithm reduced the coding length,increased variability of fl exibility,better maintained the diversity of individuals,accelerated the search and the calculation speed and convergence performance.The simulation carried on line array beam pattern null point generating and suppression for sidelobe.The result showed that the improved algorithm is compared with the traditional ones,converges more quickly,f i nd a satisfactory solution faster.
smart antenna ;beam forming;genetic algorithm
湖南省高等学校科学研究项目(11C0369)资助。
伍麟珺(1982—),女,硕士,湖南工学院电气与信息工程系讲师,主要研究方向:数字信号处理,电子线路设计。
