银行信贷和资产价格泡沫的联动性——基于动态贷款价值比的分析
2012-06-01黄飞鸣
黄飞鸣
(江西财经大学金融学院,江西 南昌 330013)
一、问题与文献回顾
现代金融市场往往是不完善的,存在信息不对称。信息不对称的存在给市场投资者的风险和收益带来了不确定性。金融的本质就是跨期的价值交换,而信息不对称使未来充满了不确定性,Jensen和Meckling(1976)[1]对不确定性所带来风险与收益不对称而导致的风险转移现象进行了研究。他们认为,引入中介代理降低因信息不对称带来的交易成本,但当交易成本大到难以用投资的收益弥补时,就会出现风险与收益的不对称。为此,银行在融资市场上实行信贷配给政策以约束投资者的融资。Jaffee和Russell(1976)率先基于不完美信息对信贷市场的配给问题进行了解释,他们提出了在现有市场利率下经济主体不能借到其意愿的贷款数量的信贷配给现象;他们指出,在实行单一贷款利率条件下,信贷市场均衡要求银行定量配给 “好”的和 “差”的借款人,才会没有人违约[2]。Stiglitz和Weiss(1981)[3]揭示了不完全信息限制条件下另一类型的信贷配给,即信贷市场不能通过利率的调整出清。他们证明了,不完全信息限制了贷款人可以创造的贷款数量;即使一些借款人愿意支付更高利率也会被完全拒绝其贷款要求。在这种情况下,银行发放贷款往往要求借款者提供一定数量的抵押物。而房地产、股票等风险资产是一种最为重要的抵押物。当资产的价格波动时,就会通过两种途径影响银行信贷的供给:一是通过直接影响抵押物价值,二是通过对银行的资产质量和银行资本金产生影响,进而影响到银行的贷款供给能力。在资产价格上涨时,银行愿意提供更多的抵押贷款,从而导致信贷扩张。投资者利用从银行借来的资金投资于风险资产,当投资收益高时,他们获得较高的回报,当投资收益低时,其风险却限于拖欠贷款、抛弃抵押物来避免进一步的损失。基于此,投资者只关心收益的增加,会高估资产价格,导致了资产价格泡沫。
虽然一些研究表明资产价格泡沫会因信息不对称和代理问题而产生 (Allen and Gorton,1993;Allen andMorris and Postlewaite,1993)[4,5], 但都没有阐明泡沫发展进程中银行系统的作用和信贷的扩张和紧缩对资产价格波动的生成机制 (Allen&Gale,2000)[6]。依照戈登方程 (Gordon equation),资产价格的 “基础价值”是由该资产潜在收益现金流的折现值所决定。然而,直到Allen-Gale模型被提出前,在实践中是很难确定一种资产的价格相对它的 “基础价值”是否已经 “超调”了。因为确定资产基础价值需要有许多假设,如,资产可能产生的现金流,用于折现的利率,以及相关风险溢价等;并且还要满足两个前提:资产供给在短期内固定、决定的资产的价值和风险确定。这是一项十分困难的工作(Herring&Watchter,1999)[7]。
Allen和Gale(2000)研究了在不确定性条件下出现的风险与收益的不对称会导致的风险转移现象,将这种风险转移应用于资产定价分析,提出基于信贷扩张的资产价格泡沫模型[6],从而打破了对资产价格为何会偏离其 “基础价值”出现过分 “超调”问题的困境。Allen与Gale(2000)认为,理性投资者用自有资金进行投资时所形成的资产价格是资产的基础价值。他们指出,当存在投资者不是全部用自有资本,而是借用银行贷款来投资时,如果其投资组合的价值高于银行贷款价值,他将获得扣除贷款本息后的剩余部分;如果其投资组合的价值不足以偿还贷款,他就会选择破产以避免更大的损失。这种收益与风险的不对称会引起投资者的风险转移行为,从而产生过度投资现象,最终导致风险资产价格高于其价值,即资产价格泡沫。瞿强 (2005)认为,Allen和Gale(2000)的研究打破了现有经典理论因假设理性的市场参与者利用自有资金追求套利均衡所带来的资产泡沫循环定义的困境。因此,从银行信贷变化着手研究资产价格就其周期性波动所带来的金融亲周期性问题才是抓住问题的本质[8]。下文将在Allen-Gale模型的基础上进一步拓展,来说明借贷投资风险资产下,银行信贷扩张对资产价格波动的冲击。
二、贷款价值比与资产价格膨胀:Allen-Gale模型扩展
(一)模型基本假设
假定存在两期,分别为t=1,2;两种资产,分别是供给可变、无风险的安全资产 (指投资收益固定,如无风险债券)和供给固定、有风险的资产 (指投资收益不固定,如投资房地产或股票或石油等);安全资产的收益率为r,决定于生产函数f(x),r=f′(x),即安全资产的回报率等于资本的边际产出;假定生产函数满足新古典假设,即对于所有的x,满足f′(x)>0,f″(x)<0,f′(0)=∞,f′(∞)=0。
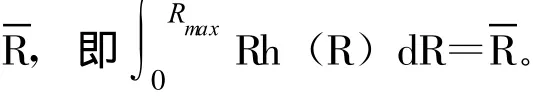
为了限制个人的投资组合的规模,并且保证在均衡状态借款者能够获得正的预期利润,我们假定投资风险资产存在一个成本C(x);这里的成本函数C(X)满足新古典假设C(0)=C′(0)=0,对所有的x>0,C′(x)>0,C″(x)>0。
投资者风险中立且个体行为不足以影响市场。他们都可以从银行借款投资于无风险资产和风险资产;充当中介的商业银行满足风险中立、古典竞争条件,其代表性银行拥有B>0单位的消费品可供贷放。
在这些假设条件下,对于中介银行而言,与投资者签订简单的债务合同是最优选择 (Gale and Hellwing,1985)[9]。投资者与银行订立简单的借贷合约:双方不能根据贷款的规模和资产的回报调整贷款条件;因此,在竞争均衡条件下,贷款的利率等于安全资产的收益率r;但是,这个简单的借贷合约使得中介银行不能识别和控制借款人的投资风险。这就会导致风险转嫁问题。在构建模型时,假定居民投资购置风险资产的效用函数都是一样的,即以总价值体现投资报酬最大化。
(二)对Allen-Gale模型的拓展
现实中投资风险资产一般采用抵押贷款的方式,即要求投资者必须有一定比例的自有资金作为保证金,其余资金可以申请贷款。设贷款占整个风险投资额的比例为α,即投资购买1单位风险资产可以从银行借入α的贷款,这里称之为贷款价值比 (loan to value),α在 [0,1]上,则自有的保证金比例为 (1-α),假设投资者在1期的自有财富为W,且满足0≤W≤B;则银行信贷资金为B-W,并假定银行无弹性的总资金供给为B,并且满足利率调整到市场出清的情况,即贷款的总需求等于可获得的 (实际)信用额。故在安全资产和风险资产的总投资不超过B。
投资者的决策问题是在1期选择从银行的借款量,然后对安全资产和房地产进行组合投资,期望在2期能取得最大投资回报。设在1期投资者分别购买XS、XR单位的无风险资产和风险资产,购买无风险资产的价格为1,风险资产的价格为P,则总的投资额是XS+PXR,为了充分利用财务杠杆,其中安全资产投资XS来源于自有资金①因为安全资产的报酬率与贷款利率相同,投资者通过贷款投资于安全资产不可能获得任何报酬,因此他不会通过银行贷款投资安全资产,并且会尽可能减少自有资金对安全资产的投资,即s是不确定的。;用在风险资产上的投资PXR,其中 (1-α)PXR来自于自有资金,α PXSR来自于银行贷款。因为投资者在安全资产上不能获得超过银行贷款成本以上的收益,安全资产的回报等于资本的边际产出、等于贷款利率即r=f′(XS)②所有的投资者是同质的,收取相同的贷款利率r。理论上讲,可以用利率限制贷款数额,但在现实中这种排他性合同是很难执行的。因此,模型对所有规模的贷款都适用同一利率r。,因此,在第2期安全资产的投资回报为rXS;而在风险资产投资上的回报是RXR,该报酬具有不确定性;则2期末应偿付的利息为r(XS+PXR),再加上投资风险资产的成本C(x),因此,在2期末投资者的净回报为:rXS+RXR-r(XS+PXR)-C(x)=RXR-rPXR-C(x)。③这里假设投资者自有资金的投资报酬等于其机会成本——无风险资产回报——利息。
投资者面临的最优化问题是通过选择向银行的贷款数量,以及用自有资金和所借贷款在风险资产和安全资产之间的配置,以便在期末获得最大化收益。在此情况下,投资者的最优投资决策问题可以归结为:

在不考虑交易成本情况下,投资者在第2期比较投资净回报与贷款成本,即比较投资风险资产的回报率R≥R*,这里R*=rα P是投资者违约临界值,当低于R*时投资者将无法偿还银行的全部贷款,而只能将拖延还贷而违约。
由于假设风险资产的持有量为1单位,风险资本市场出清的条件是:

安全资产的供给是由市场投资环境外生决定的,因此没有相应的市场出清条件。由于投资者在安全资产上不能获得额外收益,对安全资产的需求不确定,安全资产的均衡数量决定于以下方程:

(r,p,XS,XR)是资产组合 (XS,XR)对给定的参数 (r,p),且满足市场出清条件 (2)、(3)的投资决策问题 (1)的解。
(1)式对XR求导,得一阶条件为:
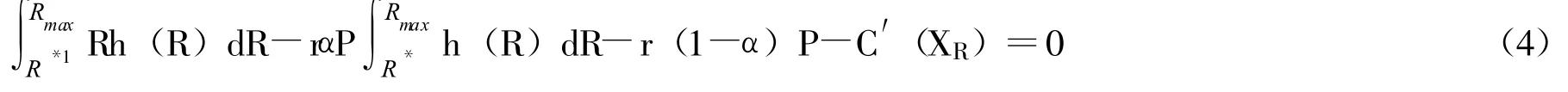
将XR=1代入 (4),可得
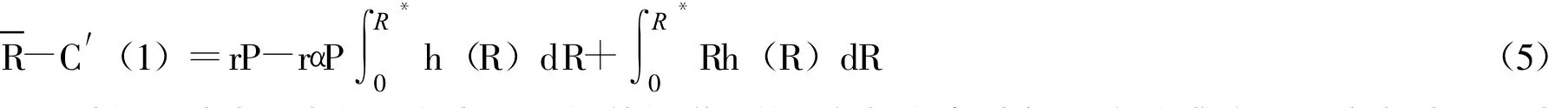
(5)式的左边为一常数,右边是rP的单调增函数。在投资者财富W和信贷总量B给定时,可以得到市场的惟一均衡条件为:(r*,P*,XS,XR)。其中r*=r=f′(XR)。则风险资产的均衡价格为:

(三)贷款价值比α对风险资产价格的影响
下面讨论贷款价值比α对风险资产价格的影响:
1.贷款价值比α=0的情况。这时投资者完全用自己的资金投资风险资产,不借贷投资,则投资者的决策问题为:

(7)式对XR求导数,得一阶条件:

进一步地,
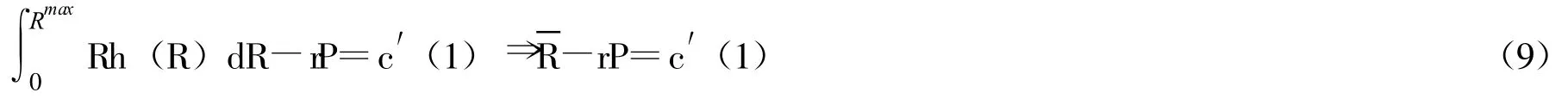
根据 (9)式和利率市场化情况下安全资产市场出清的条件 (3)式,我们得到惟一的均衡条件(r,,XS,XR),其中均衡价格为:

由式 (10),投资风险资产的基本价值可看作为其净回报的贴现值。①这与Gordon(1962)开创提出的股息贴现模型类似。详见:Gordon,M.J..The Investment Financing and Valuation of the Corporation.Homewood,Illinois:Irwin,1962.这说明只要投资者投资于风险资产的资金完全是自有资金,不管他在安全资产上的投资是否依靠贷款,对应的风险资产的均衡价格都是不含泡沫的基本价格。
2.贷款价值比α=1的情况。这时投资者完全通过借入银行资金投资风险资产。由于假设风险资产的持有量为1单位,所以贷款市场出清的条件为:XS+P=B,投资者决策问题变为:

(11)式中R*′=rP为投资有风险资产回报的临界值,低于此值投资者会选择违约赖账,将风险转移给中介银行。
对XR求导数,得:

(12)表明投资单位风险资产的预期净回报等于其边际成本。在信贷市场出清时,XS=B-PXR=B-P,由 (3)式,得:

式 (12)和 (13)决定了两个变量 (r,P)的均衡。
由 (12)式,可得

进一步可求出贷款价值比α=1时的风险资产价格:
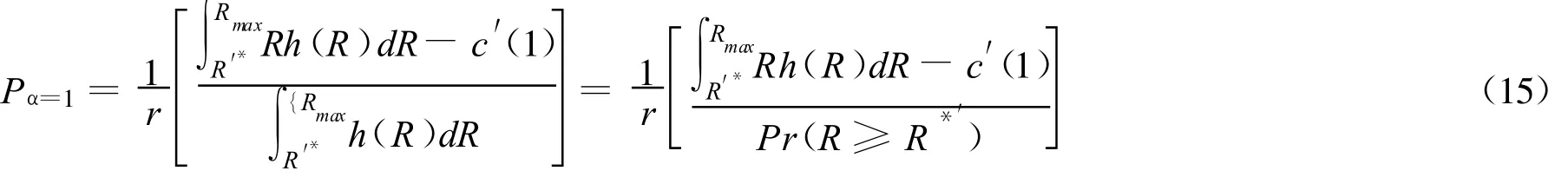

故有,Pα=1≥Pα=0。只要违约的概率为正,即Pr(R<R*′) >0,则Pα=1>Pα=0是严格的,泡沫一定存在。
1与2的比较表明:只要投资于风险资产的资金完全来自于银行,不管投资者在安全资产上的投资是否依靠贷款,对应的风险资产的均衡价格以及价格泡沫不变。风险与收益的不对称导致的风险转移,会引致投资者对风险资产的过度投资,进而带来资产价格的泡沫。①前面假设投资者是同质的,当R<R*′时,每个人都会选择违约。这就会带来银行信贷危机。但现实中,投资者不可能是同质的,只有一部分人会发生违约,但是对中介银行来说,赚取的利差收益,即便只有几个百分点的违约率也可能会给其带来大麻烦。
3.贷款价值比α在 (0,1)之间变化的情况。若保证金比例介于 (0,1)之间变动,则贷款价值比α也在 (0,1)之间变化,下面分析α动态变化将对风险资产均衡价格产生的影响。
由于r*P*是投资的贷款价值比α的函数,因此通过对 (6)式变形,得
对 (10)式和 (15)式表示的风险资产的均衡价格Pα=0和Pα=1的大小可以比较:
对 (15)式变换并简化后,可得

(17)式两边的r*p*对贷款价值比α求导数,可得


在银行信贷总量B固定时,市场均衡利率和风险资产均衡价格都是贷款价值比α的单调增函数。于是在实行抵押贷款且贷款价值比α∈(0,1)的情况下,风险资产的均衡价格高于α=0时由(10)式确定的基本价格Pα=0,而低于α=1时由 (15)式确定的均衡价格Pα=1。
在给定信贷总量B、风险资产价格分布不变的条件下,对两种不同的贷款价值比α1,α2∈(0,1),且α1<α2,则有<;由r*=f′(B-P*)可知,r是P*的单调减函数。在市场化利率下会有rα1<rα2,但是,在利率非市场化情况下,利率不会调整,只会有<2,(-) -(-)=(-)<0。这说明,贷款价值比α越高、保证金比例(1-α)越低,风险资产的市场均衡价格P也越高。
三、模拟分析
(一)贷款价值比变动的情况
为了更具体地说明问题,假设风险资产的收益h(R)服从区间 [0,4]上的均匀分布,外生的利率r=0.1,投资风险资产的成本函数为C(XR)=4。通过计算可得风险资产的基本价值及其在不同贷款价值比下的市场均衡价格、对应的价格泡沫和平均违约概率(见表1)。
从表l可以看到,在假定其他因素不变的情况下,随着贷款价值比α的下降,风险资产的市场均衡价格、价格泡沫程度和违约概率均在下降。贷款价值比α=1时,借款的投资者违约的可能为0.5,中介银行的贷款就像抛硬币定输赢,风险极高。

表1 贷款价值比动态调整与资产价格泡沫程度
现代金融市场,如外汇市场、期货、期权等衍生品市场,多实行保证金交易,借贷投资普遍存在,贷款价值比更高,杠杆高达30多倍,次贷危机爆发前美国华尔街各大投资银行就是如此。因此,本文的模型对所有杠杆化的风险投资都具适用性。
(二)利率水平和贷款价值比同时变动的情况
还应该注意的是,上述例子我们给定外生的利率r不变的情况。实际上,中央银行对利率可作调整,当利率r可调整时,它会对风险资产价格泡沫程度产生影响。我们承接上面的例子假设,如果给定贷款比率α不变、而利率水平发生变化,通过计算可得风险资产的价格泡沫程度的变化(见表2)。

表2 利率调整与资产价格泡沫程度
从表2可以看到,在假定其他因素不变的情况下,在同一贷款价值比α下,随着利率水平的变动,风险资产的基础价值、市场均衡价格、价格泡沫程度而变动;利率水平越低,风险资产的基础价值、市场均衡价格和价格泡沫程度都是越高,在同一利率水平r下,随贷款价值比α的下降,风险资产的市场均衡价格、价格泡沫程度都随之下降。但是借款投资者的违约概率并不受利率水平的影响,它只受贷款价值比α的影响,与前述例子一致——贷款价值比α越高,投资者违约概率越大。
四、结论与建议
通过引入贷款价值比对Allen-Gale模型的扩展,并以贷款价值比的动态变动分析说明其对资产价格泡沫影响的内在机理。模拟分析说明了借贷投资与资产价格泡沫的联动关系:随着贷款价值比的不断降低,风险资产的市场均衡价格、价格泡沫程度和违约概率均在下降;在贷款价值比等因素不变的情况下,利率水平越低,风险资产的基础价值、市场均衡价格和价格泡沫程度都是越高;提高利率会挤压资产价格泡沫的程度,且不会改变借款投资者的违约概率。
2010年5月中国股市开始开展融资融券业务,此前就存在信贷资金合法、违规的入市情况,Allen与Gale(2000)所描述的借贷投资和风险转移导致的过度投资和股市泡沫就会出现。在房地产市场上,由于按揭抵押贷款的盛行,Allen与Gale所揭示的资产价格泡沫最为明显。因此,本模型适用于中国房地产和股票等资产价格泡沫的形成,贷款价值比越高,泡沫越大,带给银行的违约风险也就越大。针对当前普遍存在借贷投资的房地产市场,在目前我国利率非市场化、投资者对利率不敏感的情况下,降低购房者的贷款价值比 (相应地提高首付比例)将会有效遏制对房地产的投资或投机,抑制房地产价格上升,避免更大的房地产价格泡沫,控制银行贷款的风险。
[1]Jensen,M.C.,W.H.Meckling.Theory of the Fir m:Managerial Behavior,Agency Costs and Ownership Structure[J].Journal of Financial Economics,1976,3(4):305-360.
[2]Jaffee,D.and T.Russell.Imperfect Information,Uncertainty and Credit Rationing[J].Quarterly Journal of Economics,1976,90(4).
[3]Stiglitz,J.E.and A.Weiss.Credit Rationing in Markets with Imperfect Information[J].American Economic Review,1981,71(3).
[4]Allen,F.and G.Gorton.Churning Bubbles[J].Review of Economic Studies,1993,vol.60,pp.813-836.
[5]Allen,F.,Morris,S.and A.Postlewaite.Finite Bubbles with Short Sale Constraints and Asymmetric Information[J].Journal of Economic Theory,1993,vol.61,pp.206-229.
[6]Allen,F.and D.Gale.Bubbles and Crises[J].Economic Journal,2000,(110):pp.236-255.
[7]Herring,R.and S.Wachter.Real Estate Booms and Banking Busts:An International Perspective[R].The Wharton School,Financial Institutions Center Working Paper 99-27,1999.
[8]瞿强.资产价格波动与宏观经济 [M].北京:中国人民大学出版社,2005.
[9]Gale,D.and M.Hellwig.Incentive-compatible Debt Contracts:the One-period Problem[J].Review of Economic Studies,1985,vol.52.
