基于最短路径数的WSN抗毁性评价方法
2012-06-01王鑫,李彬
王 鑫,李 彬
(西安电子科技大学理学院,陕西西安 710071)
无线传感器网络(WSN)是由一组具有感知、计算、通信和协同能力的传感器节点以Ad Hoc方式构成无线网络,能够协作地感知、采集和处理网络覆盖的地理区域中感知对象的信息,并发布给观察者[1]。WSN在多领域尤其在无人监测或环境恶劣的情况下,在对事件检测和事件跟踪中具有广阔的应用前景[2]。然而,WSN网络中的节点即传感器能量小易失效,网络中的部分节点失效会导致网络拓扑分割,降低网络的覆盖率,甚至导致整个网络失败。一般认为网络抗毁性是指网络在自身老化或者遭受打击时,导致节点失效的情况下网络拓扑结构的可靠性。衡量网络的抗毁性常用的测度指标是用最大簇大小,孤立簇和平均路径长度等来衡量网络破坏程度[3]。近年来许多学者对网络抗毁性的测度做了大量研究,文献[4]提出基于网团分层次分析大规模网络的抗毁性方案。文献[5]中介绍了基于紧密度和基于介数的抗毁性评估。文献[6]中定义了连通系数,并以此介绍了基于紧密度和基于介数的抗毁性评估。文献[6]中定义了连通系数,并以此来衡量网络的抗毁性。另外,由于小世界网络具有较小的平均路径长度和大的集聚系数的特征,故网络具有较强的抗随机打击能力,文献[7]中指出具有小世界现象的无线传感器网络具有明显的簇结构,即整个网络中出现局部的网络结构紧凑现象。文献[8]中提出的基于平均等效最短路径数的网络抗毁度适合评价WSN网络中簇的抗毁性,但对于WSN网络来说,其工作的目的是把收集到的数据发送到sink节点,相比一般网络有着更强的目的性。文献[9]根据无线传感器网络数据传输的这个特点,描述了基于有效覆盖的网络抗毁性。那么组成网络的簇的抗毁性也不能准确的反映WSN网络抗毁性。
因此,为客观地衡量WSN网络的抗毁性,文中提出基于簇有效平均等效最短路径数的抗毁性评估模型。
1 无线传感器网络抗毁性评估模型
1.1 网络模型与基本概念
布置的网络为具有小世界特性的WSN网络,如果用G表示整个网络,图G=(V,E)由m个簇G1,G2,…,Gm构成,若一个簇中任意一个节点到汇聚节点都至少有一条路,则称该簇在图G中为有效连接的。
假设WSN网络中构成后所有节点都是静止的,只有一个基站,网络中的节点均知道基站的位置。在网络形成后,网络内的节点把采集的信息传送给簇头,簇头经过数据融合以后再传送给sink节点。
WSN网络工作一段时间以后,随着节点能量的消耗或节点受到打击,而又没有任何补救措施,则当簇内部分或全部节点与sink节点之间没有通路时,网络节点将无法把数据传送给sink节点,则该簇部分或全部失效。如图1所示。
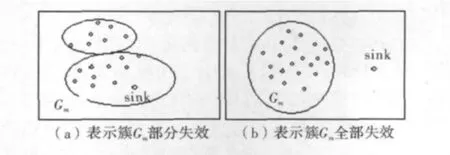
图1 该簇部分或是全部失效
1.2 网络的抗毁性评估测度
小世界网络具有较高的聚集程度和较小的平均距离的特征,文献[7]中指出具有小世界网络特征的WSN网络具有明显的簇结构,即WSN网络中簇的紧密程度较高,因此可以用平均等效最短路径数来衡量簇的抗毁度。
WSN网络由若干个簇组成的,簇即是其子网,WSN网络工作时也以簇为单元把采集的数据处理融合后再发送到sink节点。故当WSN网络节点面临不同的攻击失效时,网络中每一个簇的抗毁性也反映了整个网络的抗毁性。
簇是WSN网络工作时数据传送的单位,簇内网络节点进行通信时,首先选择最短路径,最短路径阻断时才选择更长的路径,节点间的最短路越多通信能力越强,抗毁性就越强,可见全连通网络的抗毁性是最强的,比较其他网络与全连通网络之间的差异可以衡量该网络的抗毁能力,由此文献[8]中提出了基于平均最短路径数的网络抗毁性。
定义1节点间最短路径的数量x与全连通网络节点间长度不大于k的路的数量u之比就是节点间的等效最短路经数[8],记为

若全连通网络的节点数为N,则任意节点之间不大于k的路的数量为
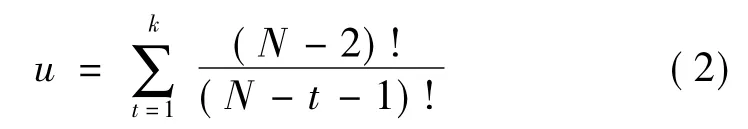
对于以数据传递为目的的WSN网络来说,簇内节点相互连接并不意味着网络就有好的抗毁性,还跟与sink节点是否连通有关,随着簇内节点受到不同的攻击,若簇内部分或全部节点与sink节点不连通,则该簇就已经部分或全部失效。只有那些与sink节点之间存在通路的部分有效。
假设WSN网络的簇有ω个连通分支,则该簇的抗毁度等于全网的有效平均等效最短路径数,记为
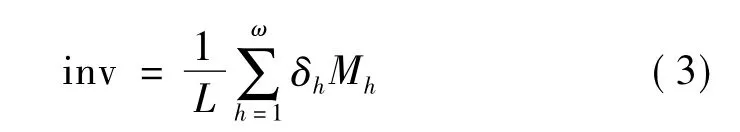
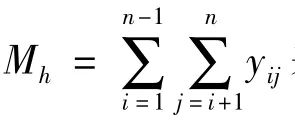
WSN网络由若干个簇组成,则整体网络的抗毁性可以用每个簇的抗毁性加权的和来衡量。
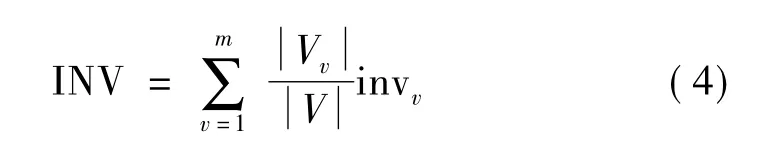
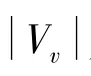
若一个WSN网络中每个簇都为全连通网络,则该WSN网络的抗毁度最大为1。
1.3 网络打击方式
无线传感器网络面临的打击方式通常有两种:随机性打击和选择性打击。随机性打击就是网络中的节点都是以一个相同的概率遭受破坏,选择性打击就是按照一定的策略,有选择地破坏网络中部分节点。
定义3(容错度)在无线传感器网络中,网络满足一定抗毁度阈值的前提下,可以随机移除网络中节点数量的最大值与网路中所有节点数目之比,称为网络节点的容错度。
定义4(抗攻击度)在无线传感器网络中,网络在满足一定抗毁度阈值的前提下,可以按照一定的策略,选择性地移除网络中节点的数量的最大值与网络中所有节点数目之比,称为网络节点的抗攻击度。
2 相关工作比较
文献[8]指出了在通信网中网络节点之间最短路越多网络的抗毁性就越强,全连通网络的抗毁性最强,通过比较其他网络自身结构与全连通网络的差异来衡量其抗毁性,提出了基于全网平均等效最短路径数的网络抗毁度,这种方法适合评估小世界网络中紧密程度高的簇的抗毁性,但没有考虑网络有效性。
文献[9]在用网络连通系数衡量网络抗毁性的基础上考虑了在WSN网络中以数据收集为中心的特征,添加了有效覆盖,提出了更准确的衡量WSN的抗毁性的新测度。但是没有利用具有小世界特征的WSN网络的簇内紧密程度高的特征。
针对具有小世界特性WSN的具体情形,考虑到WSN网络工作时以簇为单位进行数据收集,簇的紧凑程度较高,便采用簇的平均等效最短路径数来衡量全网的抗毁性,同时考虑到了簇的有效性即簇头收集的数据是否可以传递到sink节点。表1给出了相关工作的异同点。

表1 相关工作
3 仿真实验与分析
仿真在Matlab环境中进行,初始网络在500×500范围内生成200个节点,信号覆盖范围内节点相连。首先生成具有小世界特性的无线传感器网络模型[7],再采用SMCA算法[9]对网络进行分簇,对生成的网络进行随机性打击和选择性打击,之后采用介绍的测度衡量网络的抗毁度,并与文献[8]中提出的网络抗毁性测度进行比较。仿真效果如图2,图3所示。
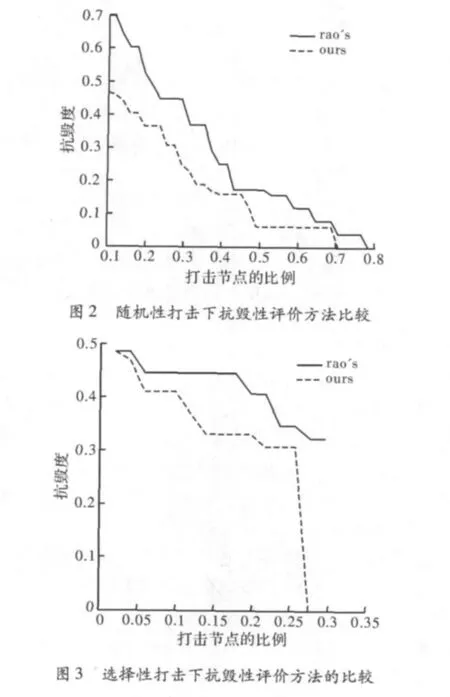
WSN节点在受到随机性打击的情况下,用文献[8]中提出的抗毁性测度评价,网络具有更好的抗毁性,但在WSN网络中是不够客观的。事实上,只有在受到随机性打击打击之后仍然与sink节点有通路的簇才是有效的,即网络抗毁性应更低,由仿真可知文中方法更具有客观性。
在选择性打击sink节点附近的网络节点时,从图3可以看出:从文献[8]的评估方法来看,网络抗毁度只是有稍微的下降,而文中的评价方法来看,网络抗毁性下降剧烈。这是因为没有节点与sink节点相连时,数据就不能传递到sink节点网络基本瘫痪。可见文中方法更有客观准确性。
4 结束语
文中在以具有小世界特性的无线传感器网络模型基础上,根据小世界网络的具有较高的聚集性和较小平均距离的特性,提出了基于有效覆盖的WSN网络的簇的平均等效最短路的抗毁性评估方法,进而用簇的抗毁性衡量整个网络的抗毁性。并对WSN网络通常面对的两种打击随机打击和选择性打击给出了两种测度容错度和抗攻度。仿真实验表明当网络受到以上两种打击时,文中的评估方法具有更强的客观性,更能准确地反应WSN网络的抗毁性。
[1]TILAK S,ABU -GHAZALEH N,HEINZELMAN W.A taxonomy of wireless micro - sensor network modle[J].Mobile Computing and Communication Review,2002,1(2):1 -8.
[2]AKYILDIZ IF,SU W,SANKARASUBRAMANIAM Y,et al.Wireless sensor network:a survey[J].Computer Networks,2002,38(4):393 -422.
[3]丁琳,谭敏生,肖炜.复杂网络抗毁性研究综述[J].电脑知识与技术,2009,5(1):51 -53.
[4]项慧慧,刘家康,匡镜明,等.大规模通信网络抗毁性评价方法[J].通信学报,2008,29(3):38 -43.
[5]陶钧,沙基昌,王晖.大规模网络存储系统数据访问抗毁性建模与评估方法[J].系统工程理论与实践,2009,5(29):158-165.
[6]吴俊,谭跃进.复杂网络抗毁性测度研究[J].系统工程学报,2005,20(2):128 -131.
[7]叶秀彩,许力,林力伟.基于小世界现象的无线传感器网络拓扑优化[J].福建师范大学学报,2008,24(5):37 -40.
[8]饶育萍,林竞羽,周东方.网络抗毁度和节点重要性的评价方法[J].计算机工程,2009,35(6):14-16.
[9]林力伟,许力,叶秀彩.一种新型WSN抗毁性评价方法及其仿真实现[J].计算机系统应用,2010,19(4):32 -36.
[10]REKA A,HAWOONG J,ALBERT - LASZLO B.Error and attack tolerance of complex networks[J].Nature,2000,406(6749):378-382.
[11]王良民,马建峰,王超.无线传感器网络拓扑的容错度与容侵度[J].电子学报,2006,34(8):1446 -1451.
