电压波动与闪变的测量方法研究
2012-06-01史三省
彭 博 周 勇 史三省
(郑州大学电气工程学院1,河南 郑州 450001;河南电力试验研究院2,河南 郑州 450052)
0 引言
为解决电网电压波动与闪变的问题,国际电工委员会(IEC)给出了电压波动与闪变的测量方法[1-2],但这种方法需要设计多个滤波器并进行多次滤波运算,实现过程较复杂[3]。而基于快速傅里叶变换(fast Fourier transform,FFT)的电压波动与闪变测量方法省略了复杂的滤波器设计,简化了计算过程[4]。故本文利用此方法实现了基于LabWindows/CVI虚拟仪器的电压波动与闪变的测量,并对测量结果进行了误差分析。通过与国际电工委员会推荐的测量方法对比,证实了基于快速傅里叶变换的测量方法是一种准确、简便、实用的离散化计算方法。
1 IEC推荐的测量方法简介
在IEC推荐的测量方法中,首先要将输入的被测电压信号u(t)调整为适合仪器内部参照水平的电压数值,再用平方检测法从被测电压信号中调解出反映电压波动的调幅波;然后用带通滤波器滤除直流分量和工频及以上的频率分量,要求对2倍工频的衰减须在90 dB以上。这个衰减作用由带通滤波器和视感度加权滤波器完成。
IEC推荐的电压波动与闪变测量原理框图如图1所示。
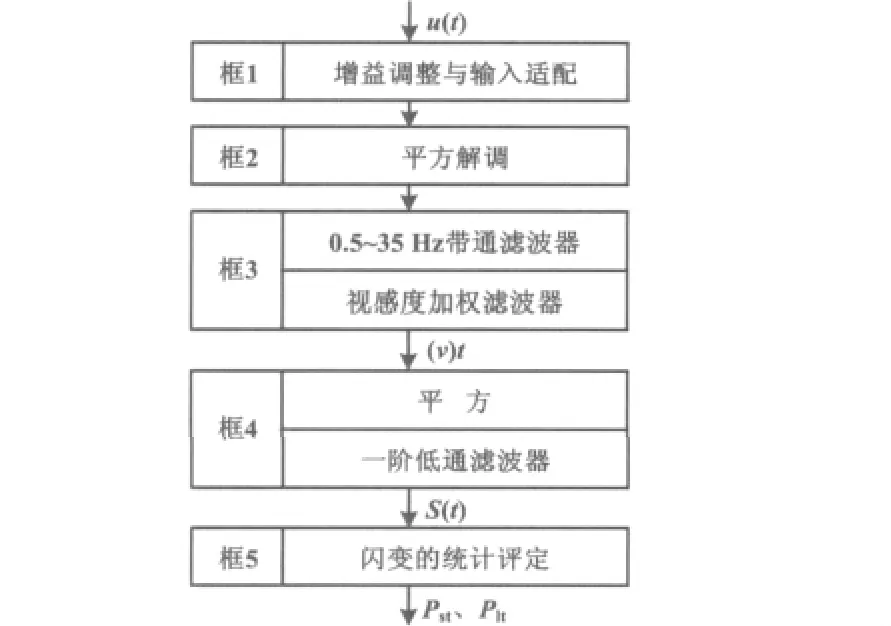
图1 IEC推荐的电压波动与闪变测量原理框图Fig.1 The principle of measuring voltage fluctuation and flicker recommended by IEC
带通滤波器分别由截止频率为0.05 Hz的高通滤波器和截止频率为35 Hz的低通滤波器构成。其中,0.05 Hz一阶高通滤波器的传递函数为:
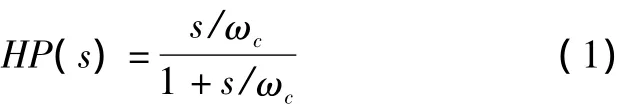
式中:s为拉氏变换的算子;ωc=2π ×0.05,为截止角频率。
35 Hz六阶巴特沃斯低通滤波器的传递函数为:
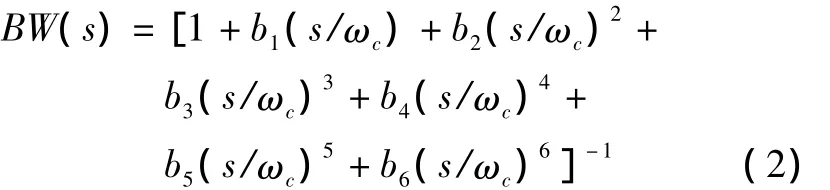
式中:ωc为截止角频率,ωc=2π ×35;bi为滤波系数(i=1,2,...,6),b1=b5=3.864、b2=b4=7.464、b3=9.141、b6=1.0。
视感度加权滤波器可模拟人眼视觉系统在白炽灯受到正弦电压波动影响下的频率响应,其IEC推荐的传递函数为:
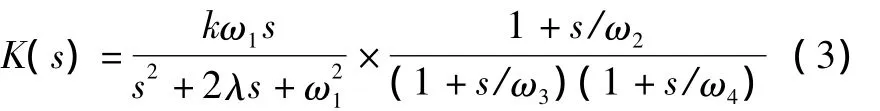
式中:k为比例系数;λ 为滤波系数;ωi(i=1,2,…,4)为各典型环节传递函数对应的截止角频率。这些系数是以5个典型环节来逼近视感度频率特性曲线,并根据均方(偏)差值最小来确定的,其中,k=1.74802,λ =2π ×4.05981,ω1=2π ×9.15494、ω2=2π ×2.27979、ω3=2π ×1.22535、ω4=2π ×21.9。
视感度加权滤波器的输出为电压波动信号v(t)。为反映光照度暂态变化的能见度,还需加入平方和积分两个滤波功能,以模拟人脑神经对视觉反映的非线性响应和记忆效应。
积分功能由一阶低通滤波器实现,其传递函数为:
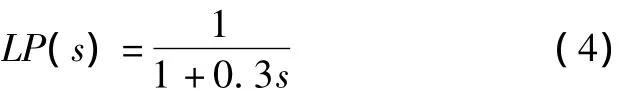
由波动信号v(t),可利用式(5)求得瞬时闪变值,即:
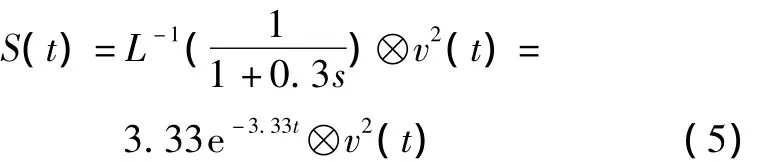
式中:⊗为卷积符号;L-1()为反拉普拉斯变换;v(t)为波动信号。
对瞬时闪变值S(t)进行等间隔采样并分级计时,可计算出累积概率函数(cumulative probability function,CPF),最后,可得到短时间闪变值 Pst和长时间闪变值Plt。
Pst的计算公式为[1]:
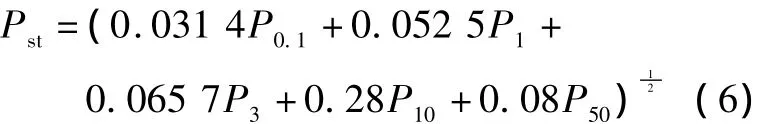
式中:P0.1、P1、P3、P10、P50分别为 10 min 内 CPF 曲线上等于0.1%、1%、3%、10%和50%时间的S(t)值。
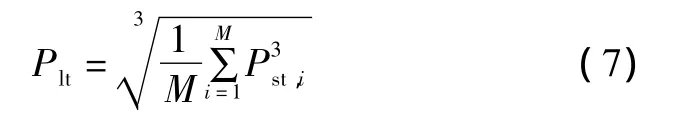
长时间闪变值Plt可由测量时间段内所包含的短时间闪变值Pst计算获得,即:式中:Pst,i为第i个短时间闪变值;M为Plt测量时间段内所包含Pst的个数。
2 基于FFT的测量方法
IEC推荐的闪变测量方法计算过程较复杂,在数字式检测装置中较难实现。基于快速傅里叶变换(FFT)的闪变测量方法则无需设计滤波器,计算过程较为简捷,其计算步骤如下[5]。
①对电压信号u(t)进行每半个周期内m点采样,得到采样信号u(n),然后利用式(8)对u(n)每半个周期求出一个电压均方根值,得到一段时间内的电压均方根值序列U(N),形成离散的电压均方根值曲线,即:
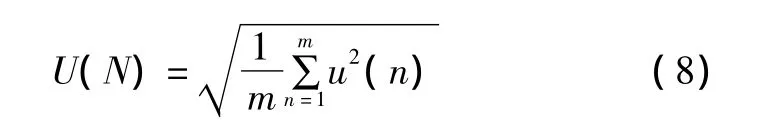
电压波动即为:

式中:Umax、Umin分别为电压均方根值的两个相邻极值;(Umax-Umin)为对应的电压波动的幅值;UN为额定电压。
②对序列U(N)进行快速傅里叶变换(FFT),求出其离散频谱。将各频率对应的频谱幅值的2倍(该频率下正弦电压均方根值曲线波动的峰峰值)除以分解出的直流分量幅值,即可得到该频率下的电压波动d(i),将d(i)代入式(10),可得该频率下的瞬时闪变值为:
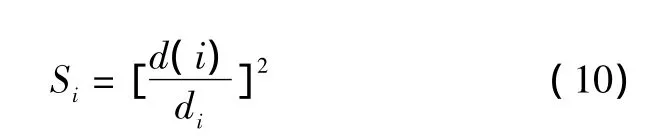
式中:di为在该频率上产生1个单位瞬时闪变值所需的电压波动。该值可从文献[5]中查得。
③因为一段波形均方根值的平方等于组成该波形的各频率分量均方根值的平方和,所以电压均方根值序列U(N)对应的瞬时闪变值S就等于其频谱上各频率对应的瞬时闪变值Si之和,即:
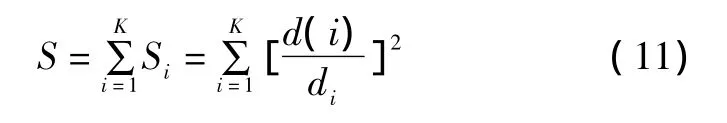
以上3个步骤构成了瞬时闪变值的离散化计算过程。利用式(6)和式(7)可计算短时间闪变值Pst和长时间闪变值Plt。需要说明的是,通过计算CPF来确定式(6)用到的5个规定值很繁琐,不利于软件编程。可采用排序法求出这5个规定值,它们分别为该段时间内S序列中的 99.9%、99%、97%、90%、50%概率大值。
3 基于FFT的测量算法的实现
3.1 软件设计
根据上述基于FFT的电压波动与闪变测量方法,采用美国国家仪器(NI)公司的LabWindows/CVI虚拟仪器开发平台[6],设计了电压波动与闪变测量软件,其流程图如图2所示。

图2 测量软件流程图Fig.2 Flowchart of the measuring software
电压波动与闪变测量软件可以实现参数设置、信号采集、电压均方根值计算及其频谱分析、电压波动和闪变值测量、结果显示以及数据存盘等功能。
在对电网电压信号采样时,需要注意以下事项。
①每半个周期内的采样点数取为m=64。
②FFT要求N值必须为2的整数次幂。
③根据加权滤波频谱特性,FFT频谱分辨率应介于0.1~1 Hz之间,即计算1个瞬时闪变值S对应的时间应在1~10 s之间。
如果每半个周期(0.01 s)求得一个电压均方根值,N 取512,则每 5.12 s(0.01 s×512=5.12 s)可计算得到一个瞬时闪变值S,10 min内大约可计算得到120个瞬时闪变值 S(5.12 s×120≈10 min)。
U(N)的频谱分辨率为 1/5.12=0.1953(Hz),U(N)的频谱分布在0~50 Hz(512×0.1953/2 Hz=50 Hz)范围内,满足闪变的最大觉察频率范围,即0.05 ~35 Hz。
3.2 算法验证及误差分析
为简化运算,假设电网电压信号为:
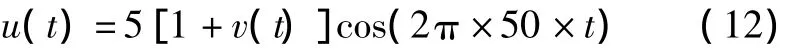
其中波动信号为:
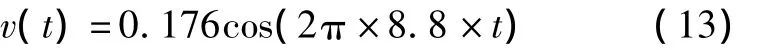
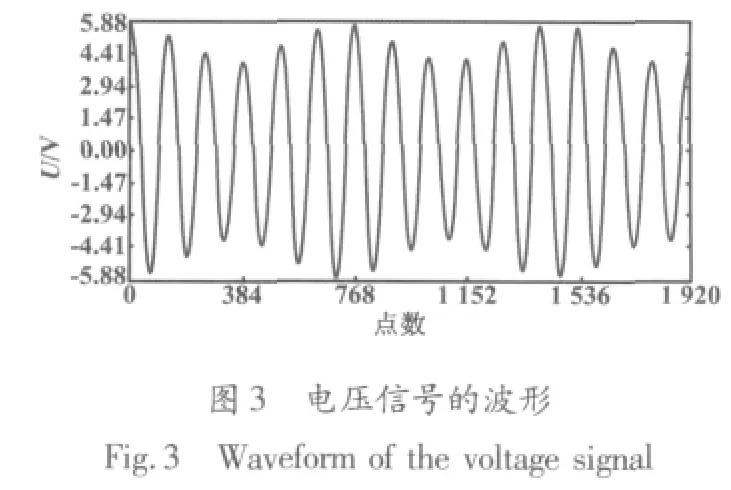
由测量软件,根据采样值绘制的电压信号波形和电压均方根值序列的频谱分别如图3和图4所示。
由图4可知,电压频谱的直流分量为3.537,该值对应于电压信号中工频分量的有效值;对应于45点的频率为8.8 Hz(45 ×0.1953 Hz),该点的幅值约为0.62,该值的2倍对应于电压波动的幅值(2×5×0.176/1.414);其余频率对应的幅值均几乎为0。最后计算的电压波动为34.475%,短时间闪变值为97.969。

查询IEC给出的单位瞬时闪变值S=1时不同频率的正弦电压波动表可知,当S=1时,8.8 Hz正弦电压波动为0.25%。
当电压波动波形、频率固定时,式(6)中的5个规定值相等,且设为S(t),代入式(6)则有:
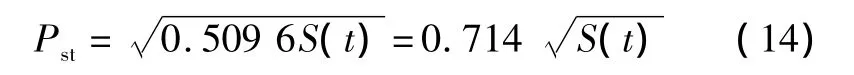
将S=1代入式(14),可得 Pst=0.714。由于34.475%/97.969≈0.25%/0.714,符合电压波动波形、频率固定时电压波动d与短时间闪变值Pst成正比的规律,从而验证了该软件的计算结果基本上是准确的。计算结果之所以会有一些误差,原因分析如下。
①采集误差
对于时域离散系统,有限的采样点数会导致还原出来的波形失真、频谱特性与原始的时域连续信号不同。因此,采样本身存在采集误差。
②频谱混叠
当采样频率fS低于原始信号最高频率fc的2倍时,原始信号中高于fS/2的频谱分量会在低于fS/2的频谱中再现,即出现频谱的混叠。这会使频谱分析出现误差。
③频谱泄漏
将无限长非周期离散的均方根值序列进行截断,限定为有限长的信号进行分析,会引起频谱的泄漏,从而导致频谱分析出现误差。
④计算误差
一方面,在求取式(6)中用到的5个规定值(P0.1、P1、P3、P10、P50)时要用到插值拟合的方法[7],这必然引入一些误差。
另一方面,在闪变计算过程中,电压波动与瞬时闪变值的关系均视为理想的线性关系,然而实际情况并非如此,这样也会产生误差。
4 结束语
电压波动与闪变测量方法的实质在于提取出电压波动分量,然后对其进行视感度加权处理,得到瞬时闪变值S(t)曲线,再对该曲线进行统计,计算出短时间闪变值Pst和长时间闪变值Plt。
本文采用基于FFT的闪变测量方法,在LabWindows/CVI虚拟仪器环境下实现了电压波动与闪变的测量,并验证了其测量结果的准确性,从而为进一步研制全数字式闪变仪奠定了基础。
[1]肖湘宁.电能质量分析与控制[M].北京:中国电力出版社,2004:85-121.
[2]高师湃,李群湛,贺建闽.基于IEC标准的闪变测试系统研究[J].电力自动化设备,2003,23(7):27 -30.
[3]袁世英,曹晖.基于 DSP的电压闪变仪的开发[J].继电器,2005,33(4):57 -70.
[4]赵刚,施围,林海雪.闪变值计算方法的研究[J].电网技术,2001,25(11):15 -18.
[5]IEC.IEC 60868-0-1991 Flickermeter part 0:Evaluation of flicker severity[S].1991.
[6]孙晓云,郭立炜,孙会琴.基于LabWindows/CVI的虚拟仪器设计与应用[M].北京:电子工业出版社,2005.
[7]赵海翔,陈默子,戴慧珠.闪变值离散化计算的误差分析及其应用[J].电网技术,2004,28(13):84 -87.
