基于七参数的AutoCAD数据坐标系统转换方案研究
2012-05-31曹健王晏彬卢云辉
曹健,王晏彬,卢云辉
(1.大连市勘察测绘研究院有限公司,辽宁大连 116061;2.中国建筑第八工程局大连公司,辽宁大连 116061)
1 背景
由于现阶段我国测绘成果的坐标系统不统一,有1954年北京坐标系、1980西安坐标系、地方独立坐标系,同时2000国家大地坐标系也于2008年7月正式启用。所以在勘察测绘行业,我们不可避免地要进行测绘成果的坐标系转换。常用的转换方法主要有四参数转换和七参数转换两种。如果地面两点的距离小于10 km,几乎可以忽略因为采用不同的椭球参数对于转换精度的影响;如果地面两点的距离超过15 km,必须考虑两种不同坐标系所采用的椭球参数,避免因椭球参数的差异,导致点位换算后精度过低。换言之,七参数是一种空间直角坐标系的转换模型,而四参数是一种平面直角坐标系的转换模型。所以,采用七参数转换方法能够很好地保证转换的精度,而在面积较大区域,四参数转换不能满足精度要求。
我们知道,很多软件都有利用七参数将一个或多个点进行转换的功能,如在ESRI公司的ArcCatalog软件中,有利用七参数将GIS格式数据进行全库转换的功能,十分方便。但是对于整个AutoCAD数据文件,进行坐标系统转换,生成另一个坐标系统的AutoCAD文件的软件却十分罕见。基于此,笔者对于这一课题进行了尝试,并且获得了很好的效果。
2 坐标系转换思路
首先选取要进行坐标转换区域的公共点,获得公共点在原坐标系统下和目标坐标系统下的三维坐标;根据控制点的坐标,通过间接平差的方法解求七参数;然后用公共点的坐标检验七参数的可靠性,如果不满足要求,则需重新计算七参数。七参数满足要求以后,转换程序打开每一个需要转换的AutoCAD数据文件,获取每一个数据文件中的每一个元素的图形坐标串以及其属性数据,然后新建一个AutoCAD数据文件,将每一个元素在原始坐标系统中的坐标串数组,经过七参数转换生成新坐标系统下的坐标串数组,附带属性数据生成新的元素,保存在新的AutoCAD数据文件中,完成坐标系统的转换。
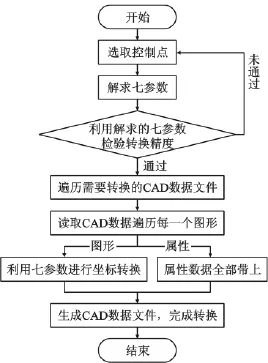
图1 坐标系转换流程图
3 解求七参数
七参数,即两个空间直角坐标系之间转换的7个参数,包括3个轴的旋转角、3个坐标增量和1个尺度因子。要解求七参数,就要至少知道3个及以上公共点的空间直角坐标(X,Y,Z)。常用的七参数解求方法主要有三种:三点法、多点法和严密平差法。当对坐标转换的精度要求不高,或者只有3个点时,可以采用三点法。当对转换的精度要求较高,而且又能提供3个以上的公共点时,可以采用多点法。当对转换的精度要求非常高时,需要采用严密平差法。由参考文献[1]可知,三点法是一种近似的七参数求解方法,对于3个公共点,按某种转换模型可以列出9个方程,取其中7个方程就能求得七参数。而多点法则利用了更多的公共点,进行平差之后可以得到更好的解算结果。设两个空间直角坐标系中有n个公共点(n〉3),它们在两个坐标系中的坐标分别为(Xi,Yi,Zi)和(),记△Xi=-Xi,△Yi=-Yi,△Zi=-Zi,认为△Xi,△Yi,△Zi是含有随机误差的观测值,并且视其为同等精度观测值,将七参数 Xi,Yi,Zi,rx,ry,rz,s作为未知数,采用W模型,按最小二乘法求解即可得七参数。但采用此法求解时是将(△Xi,△Yi,△Zi)当作等权观测值,没有考虑它们的相关性和精度差异,因而也是一种近似的求法。
严密平差法考虑(Xi,Yi,Zi)和()会受到不同的误差影响,因此它们不是等精度的观测值,也就是要将它们当作不等精度的观测值来处理。在这种情况下,转换模型除了要将七参数作为未知数外,还应取公共点在某个空间直角坐标系统中的坐标作为未知参数,然后利用转换模型建立误差方程,按照相关平差方法求解,即可得到七参数。这种方法在理论上最严密,求解精度最高,但数学模型也最复杂。上述七参数求解数学模型的计算公式,可以参照参考文献[1]。
在本项目中,笔者将一批地方独立坐标系的Auto-CAD数据文件转换成为1980西安坐标系下的成果,选择了一定数目的公共点以后,利用多点法求得七参数。为了验证该套七参数的正确性,笔者将部分公共点在地方独立坐标系中的坐标利用该套七参数,求得1980西安坐标系中的坐标,并与该公共点的已知的坐标进行比对。从下表可以看出,精度符合要求,能够作为该区域的转换七参数来使用。

利用七参数解求坐标与已知坐标对照表 表1
4 AutoCAD数据坐标系统转换
4.1 坐标系统转换的实现
在Visual Studio开发环境中,加载AutoCAD提供的类库,利用C#进行二次开发,来完成AutoCAD数据的坐标系统转换。创建 AcadApplication、AcadDocument对象,并初始化AcadModelSpace。利用其 SelectionSet获得选择集,进入第一个循环,遍历AutoCAD数据中的每一个图形,获得其属性信息。进入第二个循环,遍历该图形的每一个点,获得其在原始坐标系下的三维坐标值(X,Y,Z)original;利用七参数,即3个轴的旋转角(rx,ry,rz)、3 个坐标增量(△X,△Y,△Z)、1 个尺度因子(s)和坐标转换公式,生成该点在新坐标系统下的三维坐标值(X,Y,Z)new,完成该循环并最终形成该图形在新坐标系统下的三维坐标串数组。
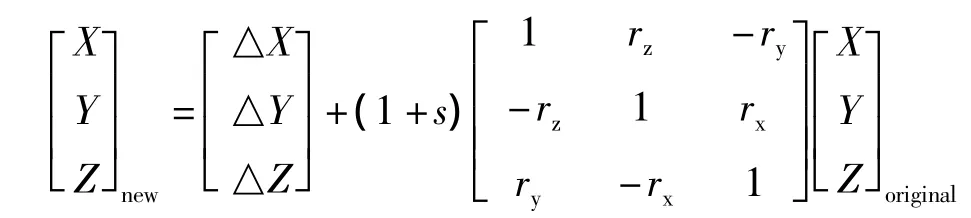
创建一个新的AutoCAD数据文件,根据在新坐标系统下的三维坐标串数组以及该对象在原AutoCAD数据中的线型、颜色、图层、字体文件、字高、倾斜角、块名、插入比例等属性信息,利用AcadModelSpace对象的 AddCircle、Add3DPoly、AddArc、InsertBlock、AddEllipse、AddLine 、AddPoint 、AddPolyline 、AddText、AddMText、AddMLine等方法[3]在新建的 AutoCAD 数据文件中生成对应的图形,即完成数据的转化[2],由于该方案的独特转换方式,属性数据无丢失,能够最大限度地保证数据的原样。
4.2 程序界面及操作
将要转换的AutoCAD原始数据文件存放到一个文件夹中,并选择该文件夹;设置目标数据文件夹,即经坐标系转换后的AutoCAD数据文件存储的位置。在系统界面中输入七参数,点击确定,如图2所示,即可完成转换。由此可见,该程序操作非常简便,没有多余的人工干预,对用户的要求低,取得了很好的效果。
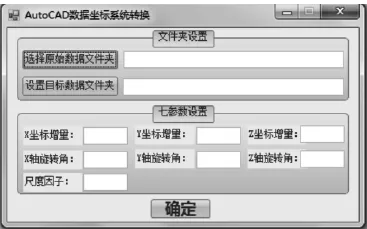
图2 系统操作界面
5 结论
(1)该方案利用公共点解求七参数,然后利用七参数进行坐标系统转换,直接将原坐标系统的Auto-CAD文件转换成目标坐标系统的AutoCAD文件,中间过程没有数据格式转换,数据属性信息无丢失,操作方便,转换效率高。
(2)该方案经过了项目的测试,应用在第二次土地调查、土地利用规划等多个项目中,经多次使用验证,转换结果精确,操作非常简便。
[1]刘大杰,施一民,过静.全球定位系统(GPS)的原理与数据处理[M].上海:同济大学出版社,1996.
[2]曹健,李国忠,徐效波等.Microstation到AutoCAD的数据转换解决方案研究[J].城市勘测,2009(1).
[3]Autodesk公司.AutoCAD2010 Develop Help.
[4]张广蔚,付新雷,肖先华等.一种三维直角坐标转换7参数模型的改进方法[J].黑龙江科技信息,2011(4).
[5]李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2005.
[6]GB/T 18314-2009.全球定位系统(GPS)测量规范[S].
