采用几何法直接计算湿球温度的研究

巫黎明

(江苏省电力设计院，江苏 南京 211102)

1 概述

湿球温度：温度计的感温球与空气直接接触所测出的空气温度称为空气的干球温度，如果用带有水分的湿纱布包在温度计的感温球上，这样的温度计就叫湿球温度计，所测出的温度就叫湿球温度，是纱布中的水与周围空气进行热、湿交换达到最终稳定状态时的温度。

气象站观测湿球温度主要是为了查算水汽压与相对湿度两个气象要素，自从江苏省气象部门在2002～2004年逐步完成建立自动观测站后，水汽压与相对湿度两个气象要素都能自动观测了，所以气象部门就不再观测湿球温度了。据了解，其他省份也是如此。

为了给火力发电厂冷却塔设计提供10%的湿球温度及相应气象条件，《电力工程气象勘测技术规程》DL/T 5158—2002中4.2.1规定：“近期连续不少于5年最炎热时期(3个月计)频率为10%的日平均湿球温度，……，其相应的日平均干球温度、相对湿度、风速、气压应选取10%的日平均湿球温度出现日的对应值。”从规定可以看出，10%的湿球温度实际上是为冷却塔水温计算确定标准，如果标准定高了，会造成冷却塔偏大，浪费钱财；如果标准定低了，那么在高温季节可能造成冷却水温过高而报警停机或降低机组出率的严重后果。因此10%的湿球温度计算非常重要。

由于气象部门在2004年以后就不再观测湿球温度这一气象要素，发电厂冷却塔参数10%湿球温度将难以直接计算，为了解决这个问题，《电力工程气象勘测技术规程》DL/T 5158—2010修订版征求意见稿4.3节提出了如下湿球温度计算公式：

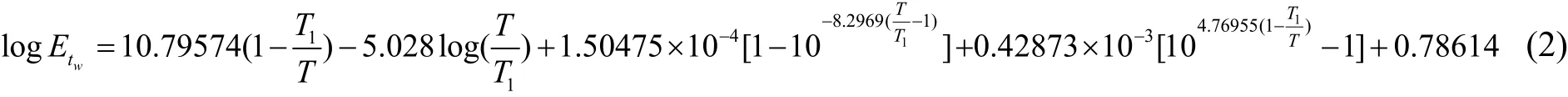
式中：tw为湿球温度，℃；td为干球温度，℃；Etw为湿球温度tw所对应的纯水平液面饱和水汽压，hPa；e为水汽压，hPa；A为干湿表系数，查表取值，℃-1；Ph为本站气压，hPa；T为绝对湿度，为湿球温度tw加上273.15，K；T1为水的三相点温度，273.16K。

条文说明4.3.2中：“……。以土耳其某电厂为例，比较2002年～2006年热季实测湿球温度和反查《湿度查算表》、差值法、相关法得到的湿球温度，93%的数据以查表法的偏差最小，最小偏差为0℃，最大偏差为0.7℃，平均偏差为0.3℃，较其它方法为佳。本条文推荐的方法即为查表法的计算公式。”

根据条文说明可以知道，目前对公式还不能直接求解，只能通过查表法、差值法、相关法来近似求解，由于这些方法效率低、易出错，且精度不高，一直以来困扰着设计工作者。近年来，也有人研究采用迭代法近似求解，但操作也比较繁琐。

2011年10月出版发行的《电力工程水文气象计算手册》8.5.3.3条也没有对“缺乏实测湿球温度”提出简单可行的计算方法。

由于湿球温度计算数据多，计算工作量大，如何简单求解以上公式？如何为发电工程水文气象行业计算累积频率10%湿球温度的确定提供论据并节约工时？带着这个问题，本人经过研究，做出了一套简单易行的计算方法，对于5年的资料，利用计算机编程，1秒左右就能完成计算；也可以在Excel中直接计算，非常方便。

2 公式的几何图形转换

将公式(1)改变为：

将式(3)两边取对数，得下式：

由于td、e、ph、A为已知，求tw，将式(2)、(4)组成一对方程组，由于两个方程中均隐含tw的未知变量，且不能直接求解。但如果假设一个tw值，就可以根据方程(2)、(4)分别计算出两个不等的logEtw值，当计算的两个logEtw值相等时，对应假设的tw值就是要求解的值。

为了便于说明，令y=logEtw、x = tw，将方程(2)、(4)进一步转化为：

采用南京气象站1999年8月17日一组实测资料(td=28.5℃ e=29.8hPa ph=1006.7hPa A=0.0007947℃-1)，因为同时观测的湿球温度总是低于干球温度，所以x值从28.5起算，步长取0.2，计算到-0.1，其对应的f1(x)、f2(x)复制到autoCAD中绘制成图，为了便于表达，将图局部放大成图1所示。从图1中可以看出，y=f1(x)、y= f2(x)是两条相交的近似直线。假设在x轴上x1处作垂直于x轴的直线分别与两条近似直线交叉于C、A两点，在 x2处作垂直于x轴的直线分别与两条近似直线交叉于G 、E两点；假设两条近似直线的交点为D，过D点作一条平行于x轴的直线分别与直线AC交于B点、与直线EG交于F点。再假设各点的坐标值分别为：C(x1，y11)、A(x1，y12)、D(x，y)、B(x1，y)、E(x2，y21)、F(x2，y)、G(x2，y22)。以下采用两种方法来进一步求解。

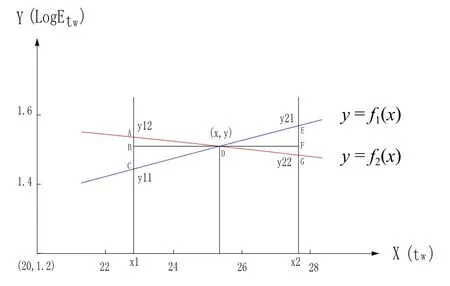
图1 y= f1(x)、y= f2(x)折线图

2.1 直接计算法

从图1、图2可以看出，方程组(5)是两条交叉近似直线，两条近似直线的交点(x,y)就是要求解的点，求解的x值就是tw。根据几何学相似三角形原理：三角形ABD与三角形DFG相似、三角形BCD与三角形DEF相似，根据相似三角形对应边长成比例的定义有：

据此可以列出如下对应的坐标数值方程组(6)：

根据方程组(5)可以求解出：

式(7)是以x1小于x、x2大于x推导的。同理，在保证式(6)的几何意义不变的情况下，x1、x2都小于x或x1、x2都大于x时式(7)均不变。

因为观测站当日实测的干球温度总是比湿球温度高，根据多站资料分析，逐日平均干球温度与湿球温度的差值在江苏省为0.2～6.5，差值的高限在南方可能偏小、在北方偏大。计算时取x2=td，x1取值范围在td-2与td-8之间都可以，x1分别取td-2、td-8所计算x值的绝对误差在0.02以内，对结果基本没有影响。

通过多站资料分析对比，取x1= td-3误差相对最小，也就是在差值0.2～6.5的中间值附近误差最小。因此在江苏省采用x2=td，x1= td-3来计算y21、y22、y11、y12的值，然后计算出x值、也就是求解的tw值。

对于湿球温度昼夜变化较大的北方地区，y=f2(x)曲率偏大，计算误差可能达到0.5℃左右，为了解决这一问题，可以缩小范围进行二次计算：令xx2=x(x为第一次计算值)，xx1=x-0.3再次代入(2)、(4)、(7)式计算，其精度即可达到0.02℃。

据此编程计算，根据连续5年夏季三个月逐日实测的td、e、ph参数来计算逐日平均湿球温度在1秒左右就可以完成，计算的精度达到0.02℃以内。也可以将式(2)、(4)、(7)编写到Excel电子表格中直接计算，非常方便。

2.2 迭代法

从图2可以看出，对应x1可以计算出Δ1=abs(y11-y12)、x2可以计算出Δ2=abs(y21-y22)，abs代表绝对值函数。当Δ趋近于0时所对应的x值就是要求的值，由于两条近似直线只有一个交点，因此迭代逐步收敛。这里介绍一种变步长迭代法，为了简单易懂，采用basic语言来表达：

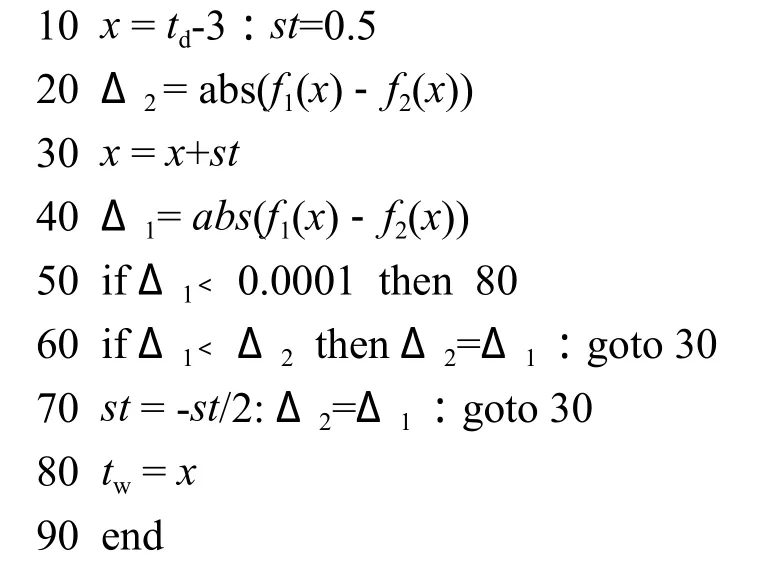
采用以上迭代计算，其初值x与步长st的取值决定迭代步数，如果初值取干球温度td、步长取5，20步以内完成计算。为了减少迭代步数，初值取td-3，步长取0.5，7～15步以内完成计算。初值的取值理由同前，目的主要是使初值尽量靠近真值，然后按照差值Δ逐渐变小的方向以每步缩减二分之一步长逼近真值。据此编程，计算连续5年夏季三个月逐日平均湿球温度在2秒左右完成。根据50行Δ1﹤0.0001结束计算条件设置，湿球温度的计算精度达到0.002℃。

由于该迭代法逐步收敛，只要初值x取值不大于干球温度且步长取值适当，迭代均可很快完成。但如果x初值大于干球温度，并使式(3)中[Aph(td- tw)+e]≤0，则程序出错。

3 误差的分析

3.1 直接计算与迭代计算误差的分析

迭代法从理论上来说计算精度最高，其计算误差小于0.0001。为了检验直接计算法的精度，本次采用江苏省13个气象站共计806组资料、对直接计算法与迭代法进行比较，以两种方法计算结果的差值绝对值来统计，结果为：平均差值在0.01℃左右，其中≤0.02℃的个数占85%，≤0.03℃的个数占96%，差值最大为0.06℃的仅有2个，差值为0.05℃的也仅有2个，差值为0.04℃的只有5个。说明两种计算方法的结果基本接近，满足湿球温度计算精度0.1℃要求。

另外，在新疆天山铝业电厂设计中，采用石河子气象站2005～2009年夏季6、7、8月共460组资料计算中，直接计算法与迭代法误差均小于0.03，完全满足设计要求。

3.2 计算值与观测值误差分析

按照地域分布均匀的原则，在江苏省选用13个气象站，采用以上直接计算法、迭代法两种方法，选用2000年7、8两个月62个实测的逐日平均td、e、ph参数来计算逐日平均湿球温度，并将逐日计算值减去逐日实测值，对差值进行统计、对比分析，其结果见表3。

表3 逐日平均湿球温度计算值与实测值统计

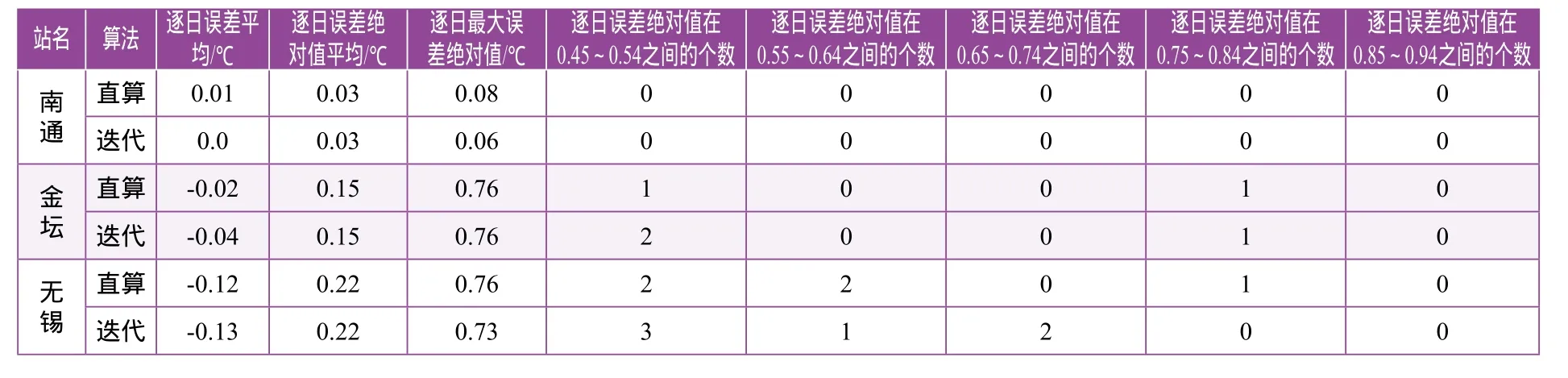
(续)

从表3可以看出，本次共分析了13个气象站共806组资料，其中有8个站逐日误差绝对值平均数较大，平均误差在0.15～0.23℃，盐城气象站与无锡气象站为0.22～0.23℃；盐城、如东、镇江、无锡4个站出现偏差，计算值比观测值偏小-0.11～ -0.21℃，其中盐城站偏小值-0.21℃；逐日误差绝对值有8个站大于0.5℃，但误差大于0.7℃的个数只有7个，其中最大值发生在宿迁，为0.87℃。

根据江苏省气候中心介绍，南京站、淮安站、南通站、徐州站是每小时观测一组数据，各要素的日平均值是24次观测值的平均值，所以代表性高，与公式符合性好；盐城站、无锡站为3次观测，日平均值是3次观测值的平均值，所以代表性就低，易产生偏差；其余站均为4次观测，代表性介于两者之间。

由于公式(1)、(2)是根据逐时观测资料建立的，当采用日平均值来计算时，采用3、次4次观测值来计算日平均值本身就存在偏差，因此采用公式计算时就会产生偏差，而采用24次观测值来计算日平均值时基本不存在偏差。

4 结语

本次研究的创新点主要是巧妙地将一组复杂的隐性方程组化解为一组近似线性方程组，并以几何学中的相似三角形原理来直接求解，解决了湿球温度求解的难题，使湿球温度的计算方法变得简单易懂。

从应用角度来看，直接计算法是对求解湿球温度这一复杂方程组的重大突破，在确保满足计算精度的情况下，计算步骤大大减少、计算过程简单，计算速度可以提高30倍以上，并可以在Excel电子表格中直接计算，满足批量数据计算，能更好的应用于工程设计，节约工时。

迭代法是传统求解隐性方程组的方法，属于试算法，本次经过线性处理后的迭代更简单明了。

[1]编写组.国家气象局.湿度查算表[M].北京：气象出版社，1986.