基于相似度的改进粗糙集模型

陶 志，郭玉燕

（中国民航大学理学院，天津 300300）

基于相似度的改进粗糙集模型

陶 志，郭玉燕

（中国民航大学理学院，天津 300300）

针对带“*”值的不完备信息系统，在对扩充粗糙集模型分析的基础上，对属性集合进行分类，引进了相似度的概念，在此基础上提出基于相似度的带有参数的改进二元关系，并讨论了基于该二元关系的粗集扩充模型,新模型更具灵活性和准确性。最后，实例分析进一步验证了改进二元关系扩充模型对处理不完备信息系统更加合理有效。

不完备信息系统；粗糙集；容差关系；相似度；改进二元关系

粗糙集理论[1]是1982年由波兰数学家Z.Pawlak提出的一种处理模糊和不确定性知识的新型数学工具。粗糙集在理论和应用上在近30年得到了很大的发展，近年来，这一理论被广泛应用到数据挖掘、模式识别等诸多领域。

但是，应用这种经典粗糙集理论的一个重要前提就是其处理的信息系统必须是完备的，即不存在属性值缺失情况，而现实中，由于数据采集能力有限等原因常常使得大量的信息系统不完备，因此，一般需对经典粗糙集理论进行必要的扩充[2]。

目前，粗糙集理论的扩充主要采用对经典粗糙集理论中相关概念在不完备信息系统下进行适当扩充。因其无需进行数据预处理，在一定程度上保留了原有系统的特征信息，从而更具有客观性[3]。使得粗糙集模型在不完备信息系统中的扩充已成为粗糙集理论发展的一个重要方向[4-6]。主要有基于容差关系[7]、非对称相似关系[8]和限制容差关系[9]等几种扩充方法。

本文分别分析了基于容差关系、非对称相似关系和限制容差关系的粗糙集模型，提出了一种基于相似度的新的二元关系，并在此基础上建立了粗集扩充模型。新模型引进了阈值，通过合理的设置阈值，可使其具有更好的分类效果。最后，通过一个实例说明，基于相似度的改进二元关系粗糙集模型对处理不完备信息系统更具有灵活性和柔韧性。

1 基本概念

1.1 不完备决策系统

形式上，S=（U，AT=C∪D，V，f）是一个四元组，其中，U是对象的非空有限集合；AT=C∪D是属性的非空有限集合，C称为条件属性集合，D称为决策属性集合，且C∩D=Ø；∀a∈AT，Va表示属性a的值域；V=∪a∈ATVa表示AT的值域；f为U×AT→V的一个映射，f（x，a）=a（x）∈Va是x在属性a上的取值。若至少存在一个属性 a∈C 使 a（x）=* ，则称 S=（U，AT=C∪D，V，f）是一个不完备的决策系统，简记为S=（U，C∪D）。

为了便于讨论，我们假定决策系统中决策属性值非空。

1.2 容差关系

文献[7]提出的容差关系认为未知属性值仅仅是被遗漏但又是确实存在的，因此，“*”被解释为一个任何可能的属性值。

定义1 在不完备决策系统S=（U，C∪D）中，由属性集A⊆C决定的容差关系为[7]

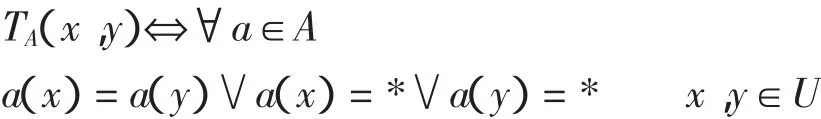
容易看出，容差关系是自反和对称的，但不一定是传递的。

在不完备决策系统S=（U，C∪D）中，对象集合X⊆U关于属性集A⊆C基于容差关系的上近似XAT、下近似和近似精度X）分别为

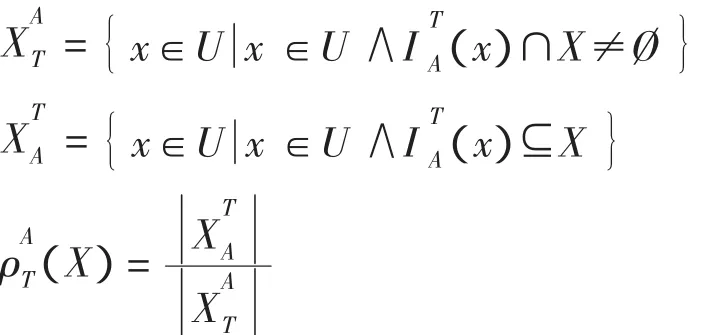
从定义可以看出，容差关系的划分粒度过粗，“*”被认为与所有已知属性值相等，因此会导致将那些没有任何明确相同的已知属性值的个体对象误判在同一容差类中，例如：x=（1，*，3，*，5，*，7，*，9），y=（*，2，*，4，*，6，*，8，*）。直观地，它们相等的可能性很小，因此，将它们认为是不可分辨而划分在同一个容差类中与实际情况不相符合。

1.3 非对称相似关系

文献[8]提出的非对称相似关系认为未知属性值“*”可能是由于知识不精确造成的，也可能是由于不能由任何一个属性值来描述。因此，不认为“*”是不确定的，而是当前不存在或者不允许比较的未知值。

定义3 在不完备决策系统S=（U，C∪D）中，由属性集A⊆C决定的非对称相似关系为[8]

定义4 在不完备决策系统S=（U，C∪D）中，非对称相似于x的对象集合RA（x）及x与之非对称相似的对象集合（x）分别为[8]

定义5 在不完备决策系统S=（U，C∪D）中，对象集合X关于属性集A⊆C基于非对称相似关系的上近似、下近似和近似精度分别为[8]

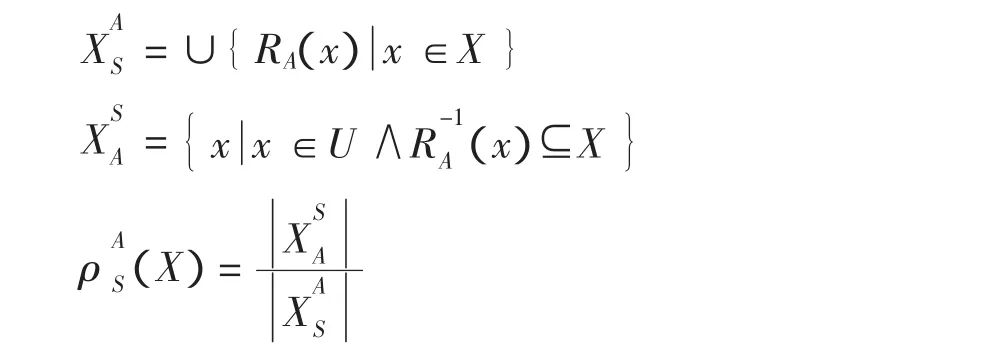
可以看出非对称相似关系具有自反性和传递性，但没有对称性。非对称相似关系也存在不足：对于某些对象之间明显有大量相同的已知属性值，直观上就可以判断为相似，但却由于不满足非对称相似关系而被划分在不同的相似类中，例如：x=（1，*，3，4，5，6，7，8，9），y=（*，2，3，4，5，6，7，8，9）。实际上，它们相同的可能性非常大，然而，根据非对称相似关系却将它们划分在不同的相似类中，这亦与实际情况不相符合。

1.4 限制容差关系

通过对容差关系和非对称相似关系的深入研究，王国胤教授认为容差关系的要求过于宽松，而非对称相似关系的要求则过于严格，从而提出了限制容差关系[9]。

定义6 在不完备决策系统S=（U，C∪D）中，由A⊆C决定的限制容差关系为[9]

显然，限制容差关系具有自反性和对称性，但不具有传递性。

在不完备决策系统S=（U，C∪D）中，对象集合X关于属性集A⊆C基于限制容差关系的上近似集、下近似集和近似精度（X）分别为

尽管基于限制容差关系的粗糙集模型与其他扩充粗糙集模型相比较有许多优点，但是它也存在着一定程度的不足。例如，x=（1，*，*，*，*，*，*，*）和 y=（1，2，*，*，*，*，*，*）仅有一个已知值相同，限制容差关系却把它们划分在同一个相似类中，但实际上这两个对象相似的可能性很小，把它们划分在同一类中过于牵强。

2 基于相似度的改进二元关系

2.1 不完备信息系统中属性分类

通过以上对不完备信息系统中几种扩充粗糙集模型的分析发现，要使不完备信息系统中的不可区分关系更加有效，需要对对象的属性值进行分析，即要对属性进行分类[10]。

定义8 设S=（U，C∪D）是不完备决策系统，任意x，y∈U，针对对象x，y，属性集C可分为以下3类：

1）绝对可区分属性

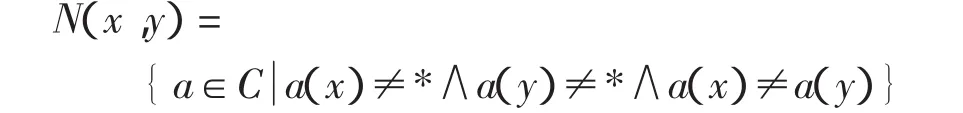
2）绝对不可区分属性

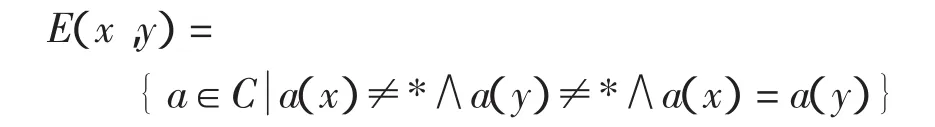
3）可能区分属性

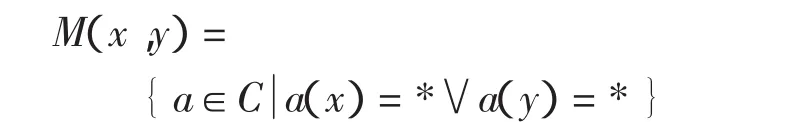
不完备决策系统S=（U，C∪D）中，未知属性值“*”等概率取值域中所有可能的值。因此，利用概率来度量两对象在含有“*”值的属性上取相同值的可能性，进而确定它们在该属性上的相似程度是合理的。基于此，我们需要先证明一个结论。

文献[11]给出相似度的概念。

定义9 给定不完备决策系统S=（U，C∪D），∀x，y∈U在属性ck∈C上的相似度为[11]

相似度仅表示对象x、y在某一个属性上的相似程度，要想准确刻画两对象间的相似度还需要考察它们在所有属性上的平均相似程度。本文通过定义平均相似程度提出了基于此相似度的二元关系。

定义10 在不完备决策系统S=（U，C∪D）中，两对象x，y∈U相似属性的平均个数为

可见，l值越大，两对象间的相似度越大，其不可区分性也越大。

2.2 基于相似度的改进二元关系

引进相似度的概念以后，我们可以重新定义新的不可区分二元关系如下：

定义11 在不完备决策系统S=（U，C∪D）中，由属性集A⊆C决定的改进的二元关系为

由定义可知，基于相似度的改进二元关系优于限制容差关系，同时，通过调整阈值α（0＜α≤1），可以很好地控制相似属性在所有属性中所占比例，从而进一步提高分类的准确度。显然，改进的二元关系是自反和对称的，但不是传递的。

在不完备决策系统S=（U，C∪D）中，改进的二元关系下对象集合X关于属性集A⊆C的下、上近似集和近似精度分别为

2.3 基于相似度的改进二元关系的相关性质

定理2 设不完备决策系统S=（U，C∪D），由属性集A⊆C决定的改进二元关系为（x，y），则对于∀X，Y⊆U有：

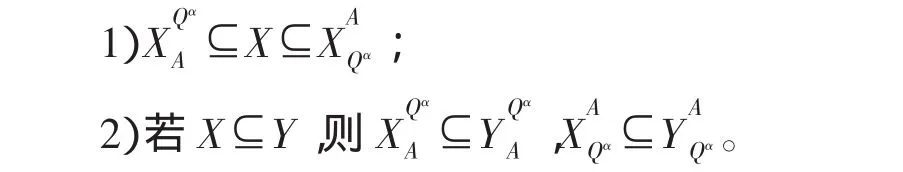
证明 由定义直接验证即得。

定理3 设不完备决策系统S=（U，C∪D），由属性集A⊆C决定的改进二元关系为QαA（x，y），若 0 ＜α≤β≤1，则有：

证明 1）因为 α≤β，所以对于∀x，y∈U（QβA（x，y）⇒（x，y）），另一方面

3 与其他关系的关联性

3.1 与容差关系

定理4 设S=（U，C∪D）为一个不完备决策系统，对于 A⊆C，X⊆U，若 α∈（0，1］，则下列关系成立：

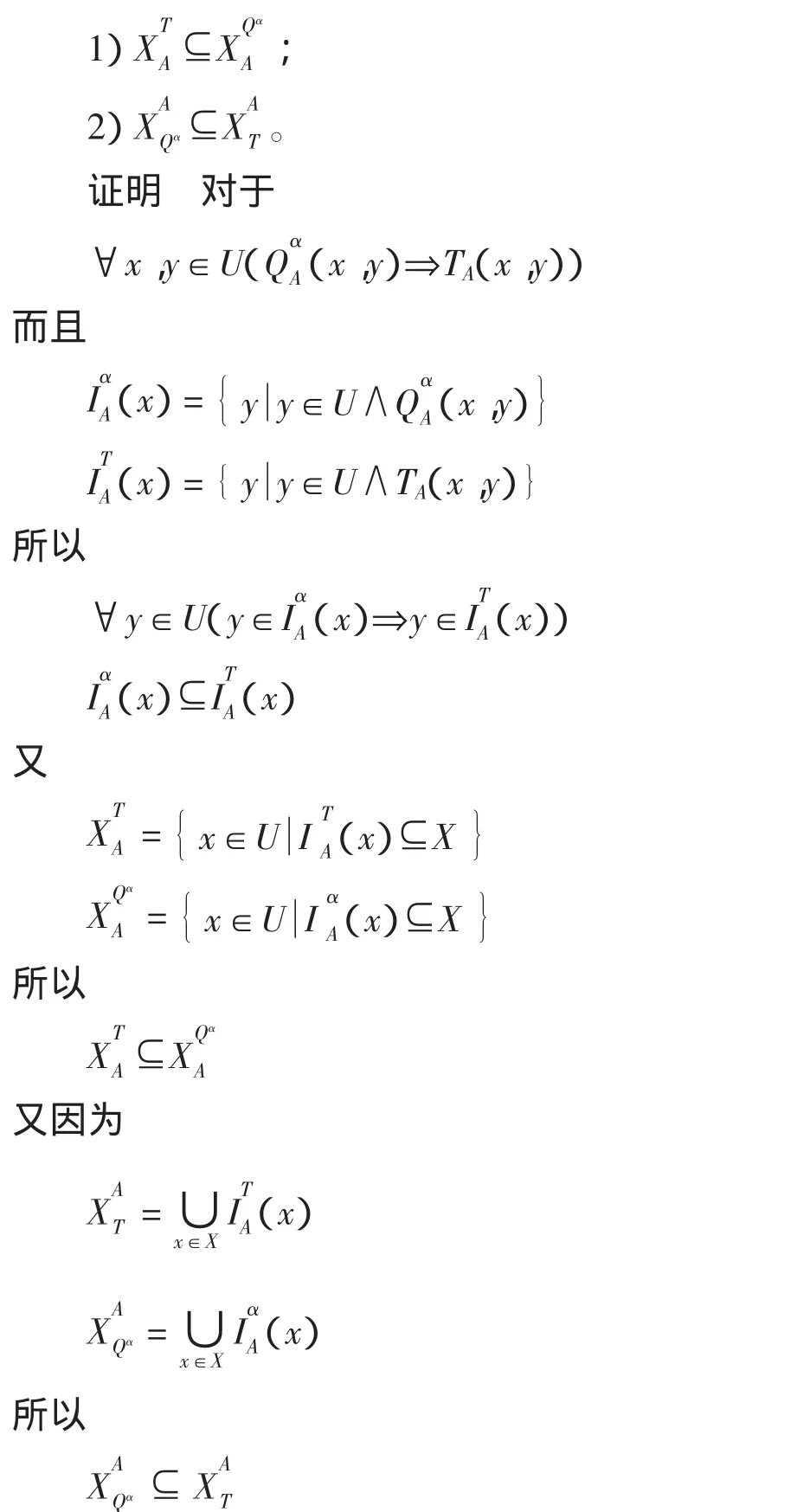
该定理说明，与容差关系相比较（无论α取何值），改进二元关系模型减少了不确定性边界，提高了分类准确性。

3.2 与限制容差关系

证明 由定义直接验证即得。

此结论说明，当选取适当的阈值α时，新模型的分类精度可高于限制容差关系的精度。

3.3 与非对称相似关系

非对称相似关系的要求过于严格，所以虽然从整体分类精度最高，但也存在着由其“刚性”要求所决定的某些固有局限性。如在1.3节中所提到的对于某些对象之间明显有大量相同的已知属性值，直观上就可以判断为相似，但却由于不满足非对称相似关系而被划分在不同的相似类中，而新二元关系由于具有可以灵活调整阈值的特点，所以恰好克服了非对称相似关系在这方面的不足。

4 实例分析

在表 1 所示的不完备决策系统中，c1、c2、c3、c4代表条件属性，其值域为[0，1，2，3]，“*”表示未知属性值，d是决策属性。

表1 不完备决策系统Tab.1 Incomplete decision system

1）根据容差关系分析表1可得如下结果

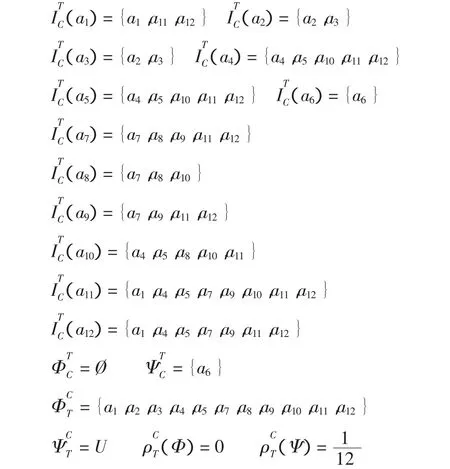
2）根据非对称相似关系分析表1可得如下结果

3）根据限制容差关系分析表1可得如下结果

4）根据改进的新二元关系分析表1如下：

上述例子进一步验证了定理4和定理5的正确性。此外，新模型不仅避免了容差关系和限制容差关系的缺陷，而且在一定程度上改进了非对称相似关系的不足，例如，a1和a11在容差关系和限制容差关系下是不可分辨的，显然过于牵强，而在本文所提改进的二元关系下，当α=0.5时，二者是可分辨的，更符合实际情况。再比如，a1和a12仅有一个属性值未知其余都相同，而在非对称相似关系下二者不能归为一类，这也不尽合理，而在基于相似度的改进二元关系下，当α=0.5时，a1和a12是不可分辨的，这一结果也符合人们的直观感觉。另一方面，从整体分类精度来看，当α=0.5时，基于相似度的改进二元关系模型的分类精度不低于非对称相似关系模型的精度，同时高于容差关系和限制容差关系模型的分类精度。

5 结语

Pawlak粗糙集理论不适用于现实的不完备数据，究其原因是由于经典粗糙集理论中不可分辨关系定义的局限性。本文在已有的几个扩充粗集模型的基础上提出了基于相似度的改进二元关系粗糙集模型，它允许用户凭借其自身对所论问题和数据所具备的相关知识来调整阈值，所得的分类结果更加符合实际情况和决策者主观期望。从文中分析还可以看出，只要合理地设置阈值，新模型比以往各种扩充粗糙集模型分类更合理，也更具有柔韧性。接下来的工作是在新模型基础上进一步研究知识约简和规则提取算法，为实际应用系统开发奠定理论基础。

[1] PAWLAK Z.Rough set[J].International Journal of Computer and Information Science，1984，11：341-356.

[2] 陶 志，王桂滨.不完备信息系统中一种改进的粗糙集模型[J].计算机工程与应用，2011，47（20）：135-137.

[3] 陶 志，王桂滨，李桂秋.一种新约束容差关系的粗糙集模型[J].中国民航大学学报，2010，28（4）：56-59.

[4]WU YUN，GUO QINGSHUN.An Extension Model of Rough Set in Incomplete Information[C]//2010 2nd International Conference on Future Computer and Communication，2010：434-438.

[5] CHEN MENG，XIA XIN.Extension of Rough Set Theory Based on Strict Similarity Relation[C]//2010 IEEE International Conference on Granular Computing，2010：666-668.

[6] 申锦标.不完备信息系统中一种拓展粗糙集模型[J].计算机应用研究，2009，26（6）：2101-2103.

[7]KRYSZKIEWICZ M.Rough set approach to incomplete information system[J].Information Science，1998，11（2）：39-49.

[8]STEFANOWSKI J，TSOUKIAS A，ZHONG N，et al.On the Extension of Rough Sets under Incomplete Information[C]//Proceedings of the 7th International Workshop on New Directions in Rough Sets，Data Mining，and Granular Soft Computing.Berlin：Springer-Verlag，1999：73-81.

[9]王国胤.Rough集理论在不完备信息系统中的扩充[J].计算机研究与发展，2002，39（10）：1238-1243.

[10] 杨霁琳，秦克云，裴 峥.不完备信息系统的不可区分关系[J].计算机工程，2010，36（13）：4-6.

[11] 王 玏.不完备信息系统的粗糙集模型[D].南昌：江西师范大学，2010.

Improvement of rough set model based on similarity degree

TAO Zhi，GUO Yu-yan
（College of Science， CAUC， Tianjin 300300， China）

Aiming at the incomplete information system with “*”， based on analysis of some extended rough set model，this paper classifies attribute set.The conception of similarity degree is introduced.A new binary relation is proposed which is based on one parameter and similarity degree，and the rough set model is based on this new relation.The extended model is more flexible and accurate.In the end， by an example， it is verified that the new extension is more reasonable and effective.

incomplete information system； rough set； tolerance relation； similarity degree； improved binary relation

TP18

A

1674－5590（2012）03－0056－06

2012-03-07；

2012-06-01

国家自然科学基金项目（60672178）；中国民航大学科研基金项目（2010kys01）

陶 志（1963—），男，辽宁沈阳人，教授，博士，研究方向为复杂系统建模、粗糙集理论及其应用等.

（责任编辑：杨媛媛）