月表微波辐射对月壤厚度及其物理温度廓线的反演

宫晓蕙 金亚秋

(复旦大学波散射与遥感信息教育部重点实验室，上海 200433)

引 言

在长期的地质演化过程中，月球表面由于火山喷发以及受到陨石小天体的撞击，形成了大量的大小不同的撞击坑形成的环形山，产生月海、月陆山脉、峭壁等起伏不平的月球表面[1]。月表层物质是由尘土、非集结性岩块、碎屑、玻璃熔融物质等构成的月壤, 包括月表面细微颗粒构成的月尘层。据研究，月海的月壤平均厚度约为4～5 m, 月陆约为10～15 m.对月壤物质结构、厚度及其分布的了解，可以为月球地质提供重要的信息，也对未来的探月、登月以及月球开发具有重要的意义。

我国2007年10月24日成功发射了第一颗探月卫星“嫦娥”1 号(CE-1)[2-3], 作为“嫦娥”1号的备份星，具有100 km更低运行轨道的“嫦娥”2号也于2010年10月1日发射升空。在“嫦娥”1号和2号的发射任务中，全球首次搭载了四通道微波辐射计，测量整个月球表面的微波辐射亮度温度[2]。CE-1微波辐射计有四个工作频率：3.0、7.8、19.35、37.0 GHz，观察角度为0°，月表面的空间分辨率约为30～50 km，测量精度为0.5 K.通过测量月表面微波辐射亮度温度(Tb)，可以反演月表层结构的月壤厚度分布，并估算月壤层中富含的氦-3(3He)含量等等[4-5]。

月表层介质的物理温度是关键的物理参数，由于月尘层热绝缘性强而月壤层的导热性较好，月表面物理温度昼夜变化极大，并随深度变化产生温度分布廓线。环形山起伏导致的月表面接受太阳光照条件的不同，使月表面物理温度表现出很大的地形差异。由于穿透深度较小，高频通道19.35与37.0 GHz的Tb对月表层温度更敏感，可用于反演月表层物理温度[6]，但是两个通道的Tb数据无法反演出多个未知量，且当两通道的Tb数据差异不大时，会产生反演的病态问题。因此，在文献[6]反演中用几处阿波罗登月点的物理温度反演值为依据，结合全月球表面物理温度随纬度分布的经验公式，确定全月球表面物理温度分布，由此反演全月球月壤层厚度和月壤3He含量。这样，月球环形山起伏使太阳光照条件不同而导致的物理温度随地形变化，以及月壤层随深度变化的物理温度分布廓线的影响等都未予以进一步的讨论。

以2007年11月到2008年2月以及2008年5月到2008年7月期间得到的1307轨CE-1观测Tb数据为基础，按相近太阳入射角的Tb数据归类为同一时刻，采用双线性插值法得到全月球白天及黑夜的Tb分布。结合月表(DEM)，特别对月球南北两极低温的物理状态进行了分析讨论。选取绕赤道一圈和沿经度150°W由南极至北极一线两个区域作为目标区域，讨论环形山地形对月表面Tb及其对物理温度反演的影响。在具物理温度分布廓线的三层月壤辐射传输的理论模型[7-8]的基础上，利用CE-1的 19.35 GHz和37.0 GHzTb数据，用最小二乘法反演月壤层呈指数形式的物理温度廓线分布；结合阿波罗登月点月壤厚度测量数据对直接影响月壤层厚度反演的3.0 GHz通道Tb进行校正，由校正后的3.0 GHz通道Tb数据进一步反演了月壤层厚度。

1. 月球两极区域辐射亮度温度与DEM/光照度

由于日月的相对位置以及很小的月球自转轴倾角，月球极区的太阳入射角比较大，月球白天太阳入射角约为60°～90°，月球黑夜太阳入射角为90°～120°，太阳入射角90°是月球白天与黑夜的分界线。

将CE-1的Tb数据(2007年11月-2008年2月和2008年5月-2008年7月)按太阳入射角选取并归组，比如：选取CE-1经过月球赤道时太阳入射角在0°～14°之间的观测数据作为月球白天中午数据，选取太阳入射角166°～180°之间的观测数据作为月球午夜时数据。可得到每个经度与纬度有4个像素点的月球极区辐射亮度温度分布，再用双线性插值方法对数据缺失的点进行插值。实际上，四个通道的Tb随地形变化的分布规律类似，仅仅在Tb的数值上有明显差异。图1(a～d)分别给出CE-1在月球北极和南极区域(60°N～90°N)黑夜的37.0 GHz 通道Tb数据与对应的DEM。DEM数据取自日本SELENE卫星激光高度计观测数据。从月表面的Tb数据分布也可看出环形山的地形轮廓。虽然Tb数据与DEM没有明确的数值上的对应关系，但DEM高的地方Tb较高；在环形山内部Tb较环形山外侧低。

图2给出了月球两极区域两个典型环形山, 即位于北极的Peary crater (88.5°N, 30°E)和位于南极的Shoemaker crater (88.1°S, 44.9°E)的Tb与DEM, 可大致看出Tb分布呈现出较强的环形山地形特征。

以日本SELENE卫星[9]2008年1月1日-2008年3月31日期间激光高度计数据，计算了月球北极和南极纬度85°以上地区的光照度。对应地，图3给出月球北极和南极85°以上区域37.0 GHzTb分布。图3(a,c)分别是月球北极和南极区域的光照度，颜色明亮的地方太阳光照度大，黑点表示全年可能接收不到太阳光照，即月球永久阴影区。图3(b, d)分别是月球北极和南极白天37.0 GHzTb分布。图中自然可看到太阳光照度低的地方，Tb也呈现低值，反之亦然。

(a) 月球北极区域的数字高程 (b) 月球北极区域的辐射亮度温度分布

(c) 月球南极区域的数字高程 (d) 月球南极区域的辐射亮度温度分布 图1 月球两极区域“嫦娥”1号获得的辐射亮度温度分布与对应的数字高程

(a) Peary 环形山 (88.5°N,30°E)辐射亮度温度与数字高程 (b) Shoemaker 环形山(88.1°S,44.9°E)辐射亮度温度与数字高程图2 “嫦娥”1号获得的极区典型环形山的辐射亮度温度与数字高程

(a) 月球北极区域光照度[9] (b) 月球北极区域37.0 GHz通道的辐射亮度温度

(c) 月球南极区域光照度[9] (d) 月球南极区域37.0 GHz通道的辐射亮度温度图3 月球两极85°以内区域太阳光照度与37.0 GHz通道辐射亮度温度的对比

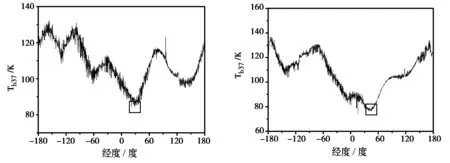
(a) 月球北极Peary 环形山(88.5°N,30°E)的辐射亮度温度 (b)月球南极Shoemaker 环形山(88.1°S,44.9°E)的辐射亮度温度图4 月球两极典型环形山的与同纬度地区辐射亮度温度的比较

选取图3(a)中北极光照度较低的环形山Peary Crater (88.5°N,30°E)，图4(a)给出了与该环形山中心位置同纬度一线上的Tb值，其中小方框标志该环形山位置。在月球南极最显著的地形特征是有三个很深的环形山，分别为Faustini (87.3°S, 77.0°E), Shoemaker (88.1°S, 44.9°E) 和一个未命名的环形山 (86.5 °S, 0 °E)[10]，从图3(c)中可看到这三个环形山与周边同纬度区域相比太阳光照度都很小，在环形山底部甚至为零。这些月球的永久阴影区被认为有可能存在固态水。图4(b)给出了与Shoemaker Crater环形山中心位置同纬度一线上的Tb值，可看到光照度较低的环形山的Tb在与同纬度区相比也是较低的，地形变化会明显影响到太阳光照度，特别是在极区，并且最终影响Tb分布。

2. 月壤层物理温度廓线和月壤厚度的反演

厚度d2月壤层具有物理温度廓线T2(z)的三层辐射传输模型如图5所示，令月尘层物理温度为T10[3]，月岩层物理温度为T3，月壤层物理温度廓线T2(z).月尘层和月壤层的有效介电常数分别为ε1和ε2，由其体密度与FeO+TiO2含量计算得到, 月岩层的有效介电常数通常取为ε3=(10+i0.5)[1].

图5 具物理温度廓线分布的月壤三层辐射传输模型

若观测角度为0°，第一层的贡献可写为[7]

Tb1=(1-r01)(1-e-κa1d1)(1+r12e-κa1d1)T10+

(1-r01)(1-r12)2r23e-κa1d1e-2κa2d2(1-

e-κa1d1)T10

(1)

月壤层深度z处厚度dz的一薄层在θ方向向上辐射, 在到达月尘层底部时可以写作

(2)

式中：κ2υ(z)是月壤层频率υ的吸收系数。为书写简单起见，积分中z均取正值。这样一薄层在π-θ方向向下的辐射写为

(3)

这部分能量在z=-d处被下垫月岩层反射(垂直或水平p极化反射率为r23p(θ))，经月壤层衰减到达月壤层表面

(4)

因此，由式(3)和式(4)，图5的月壤三层辐射传输模型到达第一层底部向上的p极化微波热辐射为

(5)

式中右边第一项为下垫月岩层的贡献，这样，观察角度为θ0时在上半空间观测到的p(=v,h)-极化辐射亮度温度为

Tbp(θ0) =t01p(θ)t12p(θ)e-κa1d1Tbp(θ，z=d1)

=[1-r01p(θ)][1-

r12p(θ)]e-κa1d1Tbp(θ,z=d1)

(6)

为研究月壤介质的热特性，Vasavada等采用一顶层厚度为2 cm的半空间模型[12]，模拟得到了热平衡状态下水星和月球近表面指数形式的温度廓线[13]。类似地，采用指数形式作为物理温度随深度变化的月壤层白天物理温度廓线为

T2(z)=Ae-βz+B

(7)

边界条件写成

T2(0)=A+B≡T10

T2(-d2)=Ae-β d2+B≡T3

(8)

式中，T1,T3分别为z=0处和下垫月岩层的物理温度(月球黑夜时的温度廓线采用负值β即可)。

求出A和B并代入式(5)和式(6), 得到0°观测角的辐射亮度温度,此时Tb=Tbh=Tbν,

Tb= (1-r01)(1-e-κa1d1)[(1+r12e-κa1d1)+

(1-r12)2r23e-κa1d1e-2κa2d2]T10+

(T10-A)(1-e-κa2d2)(1+r23e-κa2d2)}+

(1-r01(1-r12)(1-r23)e-κa1d1e-κa2d2(T10-A)

(9)

对于高频通道19.35 GHz与37.0 GHz，衰减因子e-κ1d2与e-βd2都趋近于0，因此，该两通道的式(9)简化为

Tb= (1-r01)(1-e-κa1d1)(1+r12e-κa1d1)T10+

(10)

图6 高频通道下的两层辐射传输模型

Tb37= (1-r01)(1-eκa1d1)(1+r12e-κa1d1)T10+

(11.a)

Tb19= (1-r01)(1-e-κa1d1)(1+r12e-κa1d1)T10+

(11.b)

由式(10)和式(11)可以解得

(12)

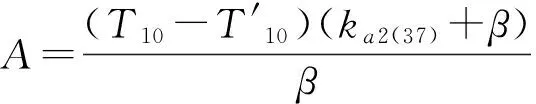
(13)

只要解得T10就可以得到月壤层的物理温度廓线。

(14)

以阿波罗15登月点为例，图8给出了由CE-1数据与上述反演方法得到的物理温度廓线，与Vasavada等给出的赤道地区物理温度廓线在2 cm以下的比较，结果吻合得较好，其中的差异可能是由于两模型中对于月尘层物理温度的不同处理引起的。

图7 阿波罗各点的物理温度以及 高频通道的辐射亮温

图8 阿波罗15点的温度扩线以及与 Vasavada等[13]结果的比较

将阿波罗登月各点的月壤厚度作为已知参数[15],通过上述反演方法得到的参数带入式(9)，可以模拟得到四个通道的辐射亮度温度。图9给出了4个通道的模拟值与CE-1观测值。可以看到在低频通道，即3.0 GHz 和7.8 GHz 模拟值(黑点)与实测值有明显的偏差。

(a) (b)

(c) (d) 图9 阿波罗各点辐射亮度温度模拟值与观测值的比较

图10 3.0 GHz通道的数据校正

图13给出赤道圈反演得到的月尘层物理温度T10与对应的DEM.可以看出:赤道圈DEM较高的月陆地区，月尘层物理温度整体较高；而在DEM较低的月海地区，月尘层温度也呈现出低值。造成反演的T10起伏的一个原因可能是最小二乘法反演T10对两参数反演很敏感。月岩层的(T10-A)反演值在230 K～250 K之间变化平缓，这可能是由于月岩层热交换达到平衡，与月表面太阳光照度等因素变化关联很小。

图11 赤道圈37 GHz辐射亮度温度与数字高程的对照

图12 赤道圈物理温度的反演

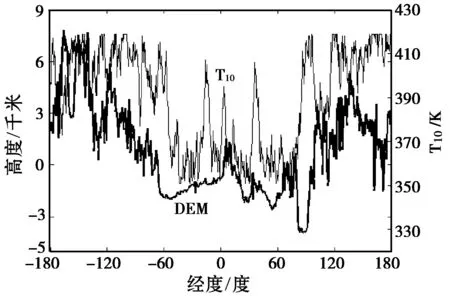
图13 赤道圈物理温度与数字高程的比较

图14给出CE-1数据反演的赤道圈月壤层温度廓线系数β与月壤层FeO+TiO2含量的对比。可以看出，在FeO+TiO2含量较高的地方，温度衰减的系数β较大，反之亦然。

反演得到的月球赤道圈月壤厚度如图15所示。月陆地区月壤厚度较大为10 m左右,与三层均匀温度的模型[6]得到的结果相似；月海的月壤厚度较小，为3～5 m.月壤厚度的变化趋势与文献[6]结果也是一致的。

用反演得到的T10,β和A和d2代入式(9)，得到模拟的辐射亮度温度。图16给出了四个通道的Tb模拟值(线)与观测值(点)的比较，其中观测值是每隔2.5°取一个样点。可以看到反演过程中所用到的三个通道观测值与模拟值非常吻合，而反演过程中未用到的7.8 GHz通道两者差别也不大，实际上这一结果也是由最小二乘法所保证了的。

现沿月球背面经度150°W提取沿该经线的Tb分布。图17给出了该区域37 GHzTb和对应处的DEM，可看到Tb基本上遵从随纬度呈余弦变化的规律。

图14 月球赤道圈反演的月壤层温度廓线系数 β与氧化亚铁与二氧化钛含量的对照

图15 月球赤道圈的月壤厚度

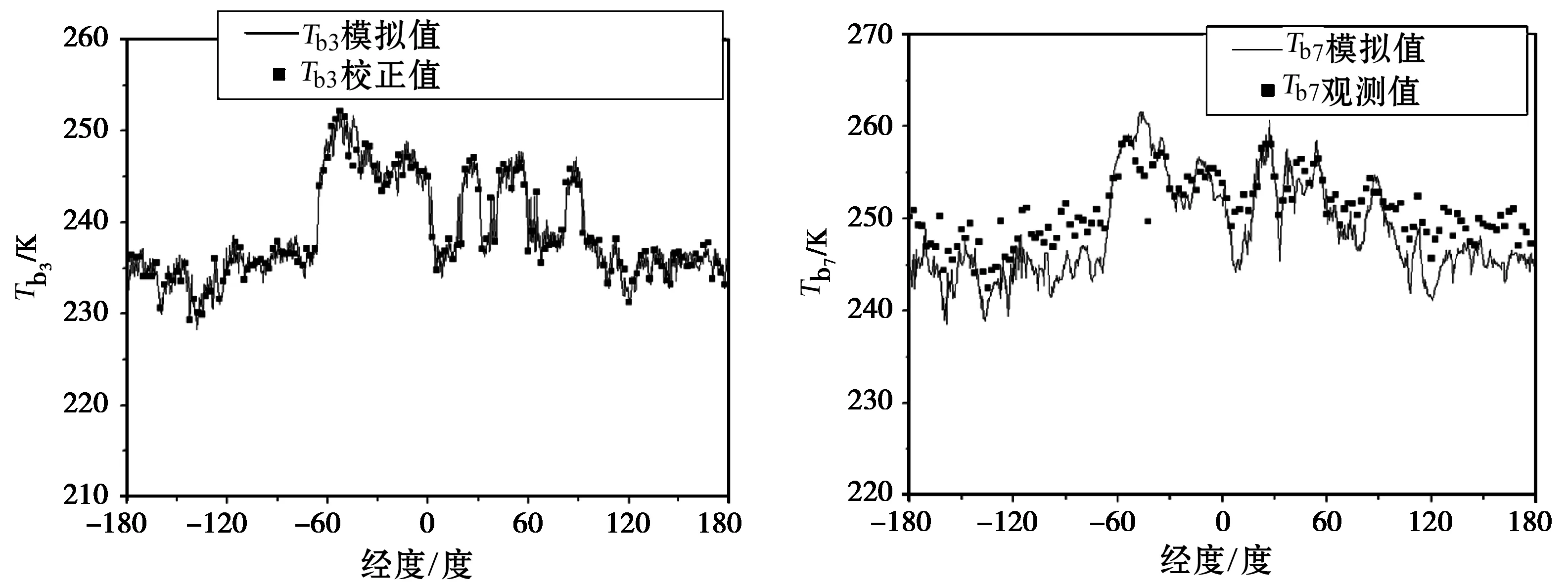
(a) (b)

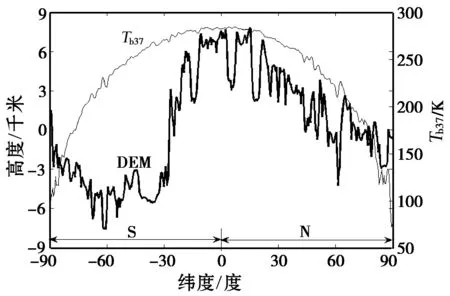
图17 沿150°W经线37.0 GHz通道辐射 亮度温度与数字高程的对照

Lawson等[16]提出了月表物理温度随纬度φ余弦变化的经验公式

T10(φ)=T10cosα(φ),α=0.25

(15)

由于在赤道圈物理温度反演时，T10取值范围分别在390 K左右，因此对同一经度不同纬度每一点处T10的变化范围设为

T10(φ)=390×cos0.2(φ)±30 K

(16)

上述指数的选取可在反演中验证修改。对于T10，±30 K也是在合理的变化范围内。反演得到的沿150°W经线的月尘层与月岩层的物理温度T10和T10-A，如图18所示。

图19给出沿150°W经线月壤层温度廓线系数β与该地月壤FeO+TiO2含量的对照。与赤道地区反演结果类似，FeO+TiO2含量高的地方，相应的β较大。

图18 沿150°W T10与T10-A的反演结果

图19 沿150°W月壤层反演的温度廓线系数β与 氧化亚铁和二氧化钛含量的对照

图20 沿150°W反演得到的月壤厚度

图20给出沿150°W反演的月壤厚度。在高纬度地区(>75°)由于Clementine的FeO+TiO2含量数据缺失，难以准确计算该地区的介电常数，月壤厚度反演值不一定可靠。在北纬中纬度地区(30°N ～70°N)，月壤厚度反演值稍高于文献[6]的反演结果，这是由于该地区的FeO+TiO2含量和β都很小，这会导致比较大的月壤厚度d2.这也证明FeO+TiO2以及月壤体密度ρ对于月壤厚度和其他参数的反演也都是非常重要的。

图21(a, b)分别给出了T10与T10-A沿不同纬度的反演值和Lawson等[16]提出的经验公式，和式(15)的比较。可以看到余弦函数形式的经验公式是合理的，但是月岩层物理温度的幂指数需要视情况作出相应的调整。

(b) 沿150°W月岩层物理温度反演值 与余弦经验公式计算值的比较图21

3. 结 论

用中国“嫦娥”1号2007年11月-2008年2月和2008年5月-2008年7月的微波辐射亮度温度观测数据，给出全月球特别是月球两极区域的4通道辐射亮度温度分布，并与日本SELENE卫星激光高度计测量得到的月表DEM以及计算得到的对应太阳光照度进行了比较，表明Tb与DEM以及太阳光照条件之间的相关性。环形山地形会影响太阳光照度分布，特别是在月球极区，环形山内部太阳光照度特别低，导致热辐射和物理温度很低。

以具物理温度廓线分布的月壤三层辐射传输模型，由阿波罗各登月处的月壤厚度以及高频通道的Tb观测数据，对3.0 GHz通道的Tb数据进行了校正。选取赤道圈和沿经度150°W为目标区域，由19.35 GHz与37.0 GHz的CE-1Tb数据反演月尘层物理温度T10与指数形式的物理温度廓线参数β,A.再由校正后的3 GHz的CE-1Tb数据，用最小二乘法反演月壤层厚度。由反演的月壤层参数T10,β,A与d2模拟的Tb与CE-1观测Tb数据吻合得很好。沿同经线的月尘层与月岩层物理温度随纬度的变化大致符合余弦经验公式幂指数规律。

结果显示：环形山地形影响太阳光照度，进而影响到热辐射，特别是在太阳光照度低的月球极区。月表面地形、物理温度廓线、介电特性(与FeO+TiO2紧密相关)以及月壤体密度是对月壤层厚度和其他热特性反演的关键参数。

致谢：本文“嫦娥”1号微波辐射计观测数据由月球探测工程中心与绕月探测工程地面应用系统提供，月表数字高程数据由日本宇宙航空研究开发机构(JASA)提供，作者在此一并致谢。

[1] HEIKEN G H, VANIMAN D T, FRENCH B M. Lunar Source-Book: A User's Guide to the Moon[M]. London: Cambridge University Press, 1991.

[2] 姜景山，金亚秋.中国微波探月研究[M].北京：科学出版社，2011

[3] FA W Z, JIN Y Q. Simulation of brightness temperature of lunar surface and inversion of the regolith layer thickness [J].Journal of Geophysical Research-Planet,2007,112(E05003): 1-13. doi: 10.1029/2006JE002751.

[4] FA W Z, JIN Y Q. Quantitative estimation of helium-3 spatial distribution in the lunar regolith layer [J]. Icarus, 2007, 71(190): 15-23.

[5] FA W Z, JIN Y Q.Global inventory of helium-3 in lunar regolith estimated by multi-channel microwave radiometer on Chang-E 1[J].Chinese Science Bulletin, 2010,55(35): 4005-4009.

[6] FA W Z , JIN Y Q. "A primary analysis of microwave brightness temperature of lunar surface from Chang-E 1 multi-channel radiometer observation and inversion of regolith layer thickness", Icarus, 2010, 207: 605-615.

[7] JIN Y Q. Electromagnetic Scattering Modelling for Quantitative Remote Sensing [M]. Singapore: World Scientific, 1994.

[8] JIN Y Q,FA W Z..The modeling analysis for microwave emission from stratified media of non-uniform lunar cratered terrain surface in Chinese Chang-E 1 observation[J]. IEEE Geoscience and Remote Sensing Letters, 2010 (3): 530-534.

[9] NODA H, ARAKI H, GOOSSENS S,et al.Illumination conditions at the lunar polar regions by KAGUYA(SELENE) laser altimeter[J]. Geophysical Research Letters,2008,35,L24203, doi: 10.1029/2008GL035692.

[10] LUCEY P G. The poles of the moon[J].Elements, 2009, 5(1): 41-46.

[11] JIN Y Q, FA W Z. An inversion approach for lunar regolith layer thickness using optical albedo data and microwave emission simulation[J]. Acta Astronautica, 2009, 65(9): 1409-1423.

[12] MITCHELL D L, de PATER I . Microwave imaging of mercury's thermal emission at wavelengths from 0.3 to 20.5cm[J]. Icarus, 1994, 110: 2-32.

[13] VASAVADA, A R, PAIGE D A, WOOD S E. Near-Surface temperatures on mercury and the moon and the stability of polar ice deposites[J].Icarus, 1999(2), 141: 179-193.

[14] MCKAY D, HEIKEN G, BASU A, et al. The lunar regolith[M]// HEIKEN G H, VANIMAN D T, FRENCH B M. Lunar Source-Book . New York :Cambridge Univ Press., 1991, 285-356.

[15] SHKURATOV Y G, BONDARENKO N V. Regolith layer thickness mapping of the moon by radar and optical data[J]., Icarus,2001, 149(2):329-338.

[16] LAWSON S L, JAKOSKY B M, PARK H S, et al. Brightness temperatures of the lunar surface: Calibration and global analysis of the Clementine longwave infrared camera data[J]. J Geophys Res, 2000, 105(E2): 4273-4290.