长春和新乡雨衰时间序列的马尔科夫链模拟
2012-05-29杨瑞科赵振维
李 磊 杨瑞科 赵振维
(1.西安电子科技大学理学院,陕西 西安 710071;2.中国电波传播研究所 电波环境特性及模化技术重点实验室,山东 青岛 266107)
引 言
随着卫星通信的发展及终端用户业务需求量的加大,通信容量不断提高,低频段变得越来越拥挤,因此,具有较大带宽和较高频谱的Ku(14/12 GHz)及以上波段的卫星通信系统越来越受到人们的重视。然而Ku以上波段的通信易受降雨影响,在强降雨时,可使链路中断。要保证信息传输的有效性,仅靠传统的加大链路余量的方法是远远不够的,因此需要采用自适应衰落削减技术(FMTs)来对抗这些传播损失[1]。为了使FMTs更好的应用于实际卫星通信链路,需清楚了解此波段的雨衰时间特性。采用传播实验来分析雨衰减的动态特性难以实现、成本较高,且只能适用于某特定链路,局限性较大。通过计算机模拟雨衰减时间序列成本低、易实现,且能根据卫星通信系统的频段来模拟相应的雨衰时间序列,可操作性高。
80年代初,Maseng和Bakken基于一阶马尔科夫理论提出了一种模拟雨衰减特性的模型(M-B模型)[2]。90年代末,法国航空航天和国立太空科学研究中心(ONERA CNES)对M-B模型进行了改进,提出了一种可按要求产生降雨事件的模型(E-M-B模型)[3]。2001年欧洲合作科技研究联盟(COST)在报告COST 280中将上述时间序列发生器模型用在毫米波无线电系统的传播损耗削减方案中[4]。在国内,关于雨衰静态特性的研究较多[5-7],目前,赵振维[8]等人基于雨胞分布提出了一种雨衰减预报模型,杨瑞科[9]等利用E-M-B模型对我国典型地区的雨衰减时间序列进行了仿真研究,对我国雨衰动态特性的研究和发展具有重要的实际意义。
N阶马尔科夫链模型是利用马尔科夫理论建立的一种模拟雨衰时间序列的模型,可按照给定的持续时间和最大衰落深度来产生满足要求的降雨事件[10],此模型基于国际电信联盟无线电通信研究组(ITU-R)推荐的Van de Kamp衰落斜率模型,可应用于世界大多数地区[11]。利用N阶马尔科夫链模型模拟了长春和新乡地区的降雨衰减时间序列,对其概率分布进行了统计分析,并与ITU-R提供的这两个雨区时间百分概率进行了比较研究。
1. N阶马尔科夫链微观模型
1.1 转移矩阵的定义

(1)
(2)
式中:pij表示从衰减值Ai至Aj的概率,矩阵模型实例如图1所示[12]。

图1 N阶马尔科夫链模型的稳态和 转移概率示意图


图2 N阶衰减事件示意图
1.2 状态转移矩阵参数
1) 衰落斜率
衰落斜率是指衰落随时间变化的速率,其概率分布取决于气候参数、雨滴大小分布。衰落斜率的预测分布由衰减电平A(t)和时间间隔长度Δt以及能够从信号中滤除对流层闪烁和雨衰快速变化的低通滤波器的3 dB截止频率决定。该模型经滤波后在某一时间点上的衰落斜率ζ定义为[11]
(4)
2) 衰落斜率条件概率密度函数(CPDF)
衰落斜率的条件概率密度P(ζ|A)可由Van de Kamp衰落斜率模型计算得出。可应用于仰角为8~52°,频率为10~30 GHz的卫星通信链路中[11],其表达式为
(5)
σζ表示某一特定衰减电平时的条件衰落斜率的标准偏差,
σζ=sF(fB,Δt)AdB/s
(6)
当仰角在10°和50°之间时,s在欧、美洲的平均值为0.01,模拟中同样采用0.01;F为低通滤波器和采样时间的函数,
(7)
式中:b=2.3,低通滤波器3 dB截止频率实验结果表明当fB=0.02 Hz时,能够充分的滤除对流层闪烁和雨衰的快速变化。
图3给出了利用Van de Kamp衰落斜率模型计算出的四个不同衰减值的衰落斜率的条件概率。从而可得出N阶马尔科夫链模型的转移概率[13],其示意图如图4所示。

图3 不同衰减值衰落斜率的条件概率密度

图4 状态转移概率
3) 状态转移矩阵参数
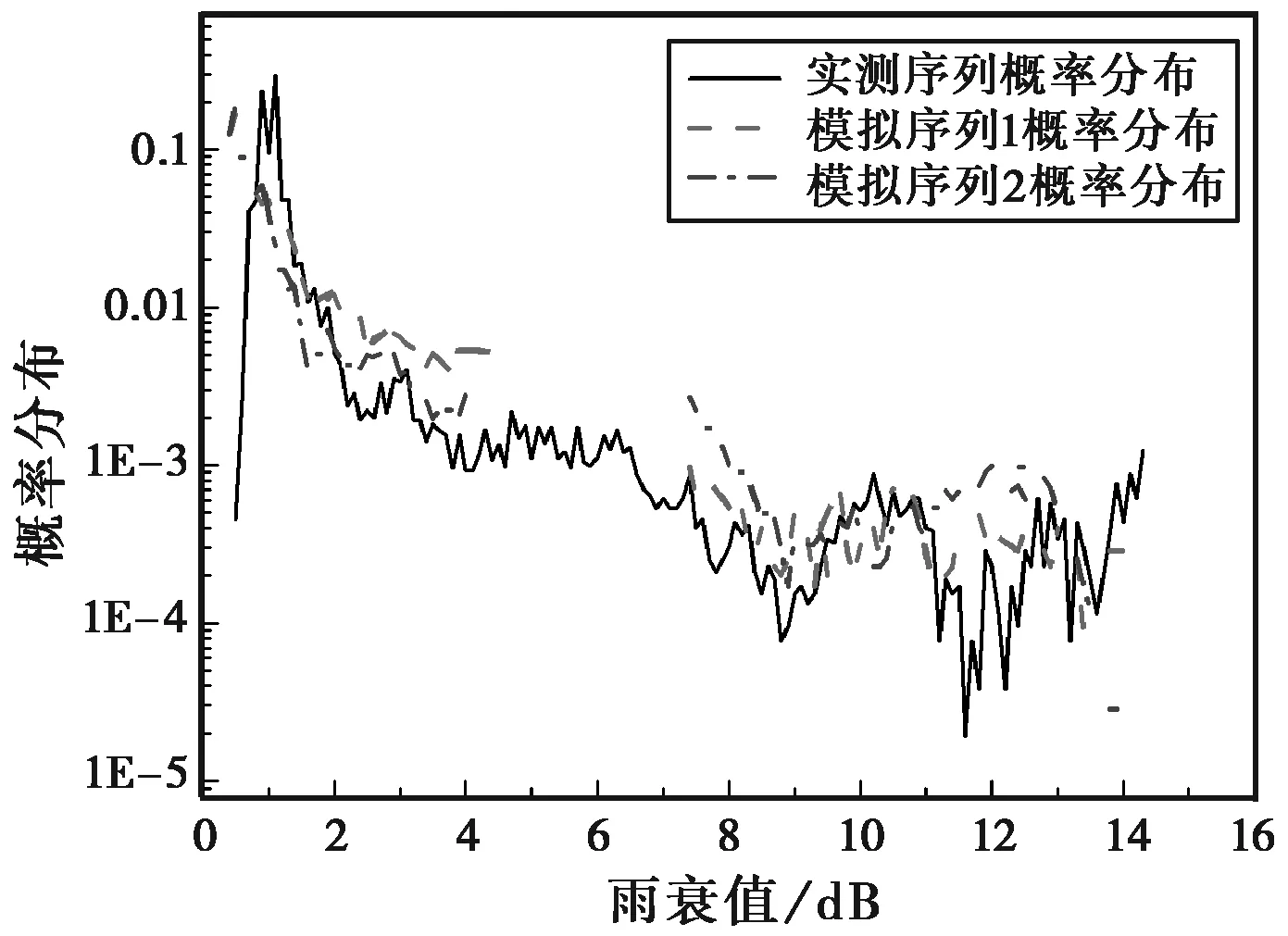
要计算式(2)所示的状态转移矩阵,需先计算由当前状态转移Ai到下一个状态Aj的概率pij,如图4,ζk=(Ai+1-Ai)/2,pi,i+k表示P(ζk=(Ai+k-Ai)/2|Ai)的值,其中j=i±k.因此,能够描述雨衰改变速率的衰落斜率,ζ(dB/s),可以用来填充这个状态转移矩阵[10]。两个状态衰减值之间的转换满足下列规则:当|ζ·δt| (8) 式中kmax=ζmax·δt/da取整数。 图5和图7分别为利用频率为12.5 GHz信标测量的长春2010年7月27日晚和新乡2010年8月10日凌晨的两场降雨的雨衰时间序列。测得此序列的最大衰落深度分别为:0.40~14.3 dB,0.30~12.95 dB,衰减间隔da=0.01 dB,时间采样周期1 s.根据其实测衰落深度和持续时间,利用式(8)求出N阶马尔科夫链模型在各状态的转移概率,随后利用N阶马尔科夫链模型分别模拟了两场降雨的衰减时间序列,如图6和图8所示。 图5 长春实测降雨衰减时间序列 图6 长春模拟降雨衰减时间序列 图7 新乡实测降雨衰减时间序列 图8 新乡模拟降雨衰减时间序列 从图5~图8可以看出,N阶马尔科夫链模型可按照给定的衰落持续时间和最大衰落深度模拟出相应的与实测雨衰序列相似的时间序列。 无论初始衰减值为多少,只要时间足够长,N阶马尔科夫链的每一个状态衰减值的概率分布都可以在时间序列中体现出来。根据马尔科夫链的遍历性[14],对于固定的状态j,不管链在某一时刻从什么状态出发,通过长时间的转移,到达状态i的概率都趋近于一个固定值πi,因此, (9) 构成一分布律,称为N阶马尔科夫链的极限分布,其矩阵表达式为 (10) (11) 1) 实测和模拟雨衰时间序列的比较 图9 长春实测与模拟比较 图10 新乡实测与模拟比较 2) ITU-R和模拟雨衰序列统计概率比较 为了验证N阶马尔科夫链微观模型的可用性,仅通过与单个实测雨衰序列的比较是远远不够的,必须进行多个模拟样本序列的统计分析。因此,根据ITU-R提供的长春和新乡所在雨区及其年0.01%概率降雨率(如表1),利用N阶马尔科夫链模型分别模拟了50组雨衰时间序列,统计其概率分布,并与ITU-R提供的卫星轨道位置为92°E、频率为12.5 GHz在线极化情况下的雨衰概率分布进行了比较,如图11和图12所示。 表1 长春和新乡所在雨区及0.01%概率降雨率 图11和12的比较结果表明:当降雨衰减较小时,利用N阶马尔科夫链模型模拟的雨衰时间序列的概率分布与ITU-R提供的降雨时间百分概率分布一致性很好,当发生小概率降雨事件时,两者会出现一定偏差。由于在大部分时间百分概率下,两者比较一致,从而进一步验证了N阶马尔科夫链微观模型在我国的可用性。 图11 长春模拟和ITU-R衰减时间概率比较 图12 新乡模拟和ITU-R衰减时间概率比较 基于马尔科夫理论建立的N阶马尔科夫链模型,模拟了长春和新乡地区的雨衰时间序列并分别与两个地区的实测雨衰序列进行了比较,结果表明,此模型可以模拟出与实测雨衰时间序列相似性较好的序列。 为了验证此模型的可用性,统计比较了长春和新乡地区单个模拟和实测序列的概率分布以及转移矩阵的稳态概率分布。随后进一步的对这两个地区50组模拟雨衰时间序列的概率分布进行了统计分析,并与ITU-R提供的卫星位置为92°E、频率12.5 GHz线极化情况下这两个地区的不同降雨衰减值下的时间百分概率进行了比较。结果表明:在大多时间概率下,模拟序列的概率分布与实测或ITU-R给出的概率分布基本吻合,只有当小概率事件时,由于实测和模拟数据较少,会出现一定偏差,从而表明该模型在我国的可用性。 [1] LACOSTE F. Classical and on-demand rain attenuation time series synthesis: principle and applications[C]//Proceedings of 24th AIAA ICSSC Conference. San Diego, California, June, 2006: 1-10. [2] MASENG T, BAKKEN P M. A stochastic dynamic model of rain attenuation[J]. IEEE Trans on Commun, 1981, 29(5): 660-669. [3] CARRIE G, LACOSTE F, CASTANET L. A new 'event-on-demand' synthesizer of rain attenuation time series at Ku-, Ka- and Q/V-bands[J]. International Journal of Satellite Communications and Networking, 2009, DOI: 10.1002/sat, 1-17. [4] FILIP M. COST 280: Propagation Impairment Mitigation for Millimeter Wave Radio Systems[R]. Stevenage: IEE Micharl Faraday House, 2003, 573-576. [5] 车 晴, 毛 志. Ku波段卫星广播中雨衰现象的研究[J].电波科学学报, 1999, 14(2): 76-81. CHE Qing, MAO Zhi. Study of the rain attenuation in the satellite broadcast of Ku band[J]. Chinese Journal of Radio Science, 1999, 14(2): 76-81.(in Chinese) [6] YANG Ruike, WU Zhensen. Rain attenuation ratios on short microwave and millimeter wave band earth-space paths[J]. International Journal of Infrared and Millimeter Waves, 2003, 24(12): 2163-2172. [7] 赵振维, 吴春雨, 林乐科, 等. 视距链路的雨衰减预报模式研究[J]. 电波科学学报, 2006, 21(5): 656-658. ZHAO Zhenwei, WU Chunyu. LIN Leke, et al. A new prediction model of rain attenuation of terrestrial line-of-sight systems[J]. Chinese Journal of Radio Science, 2006, 21(5): 656-658. (in Chinese) [8] 赵振维, 卢昌胜, 林乐科. 基于雨胞分布的视距链路雨衰减预报模型[J]. 电波科学学报, 2009, 24(4): 627-631. ZHAO Zhenwei, LU Changsheng, LIN Leke. Prediction model of rain attenuation based on the EXCELL rain cell model for the terrestrial line-of-sight systems[J]. Chinese Journal of Radio Science, 2009, 24 (4): 627-631. (in Chinese) [9] 杨瑞科, 李 磊, 仲 普, 等. 我国典型地区动态雨衰减时间序列仿真研究[J]. 电波科学学报, 2011, 26 (5): 875-880. YANG Ruike, LI Lei, ZHONG Pu, et al. Simulation of dynamic rain attenuation time series at typical regions of China[J]. Chinese Journal of Radio Science, 2011, 26 (5): 875-880.(in Chinese) [10] CASTANET L, DELOUES T. Channel modeling based on n-state markov chain for stacom systems simulation[C]//ICAP 2003 Conference. Exeter, UK, 2003: 119-122. [11] International Telecommunication Union. ITU-R P.1623.1 Recommendation: Prediction method of fade dynamics on Earth-space paths[R]. Geneva: ITU, 2003. [12] HEDER B. General N-state Markov model applicable for attenuation time series generation parameterized from Gaussian fade slope model[C]//WSEAS-EHAC Conference. Madrid, Spain, February 2006. [13] HEDER B. Rain attenuation time series generation applying N-State Markov Model parameterized from Hungarian measurement[C]// ESTEC Conference. Noordwijk, Novomber, 2005. [14] 盛 骤, 谢式千, 潘承毅. 概率论与数理统计[M]. 北京: 高等教育出版社, 2004.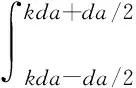
1.3 雨衰序列的模拟及与实测序列比较




2. N阶马尔科夫链模型的验证
2.1 N阶马尔科夫链的性质

2.2 N阶马尔科夫链模型的验证






3. 结果和结论
