二级模糊综合评判法在远程教育量化考核中的应用
2012-05-28杨红梅
□杨红梅
( 山西广播电视大学,山西 太原 030027)
一、引言
中央广播电视大学(简称中央电大)是一个以中央电大为龙头、44所省级电大和2000多个学习中心为支撑的、以开展现代远程教育为己任的一所新型大学。山西广播电视大学(简称山西电大)是由山西省政府主办、山西省教育厅主管,接受中央电大业务指导,以卫星、电视和互联网为主要载体进行学历继续教育和非学历继续教育,是依托系统(已遍布全省90%以上的县市120多个分校和教学点)、以远程教育为主要手段办学的公益性高等学校。
对于这个4级办学的电大系统来说,它的考核评价体系的建立和完善尤显复杂和重要。随着电大远程教育由试点工作转化为常规工作,考核工作的量化越来越受到人们的关注。无论是对分校的考核还是对教学点的考核,都是以考核评价结果作为依据的,考核评价结果作为教学管理最重要的活动之一,对于完善远程教育运行机制,提高电大教学管理的水平至关重要。
在考核评价活动中,由于考评对象颇多,考核指标也不少,同时又存在着许多不确定的现象,而这些不确定的现象其原因是在于评价结果差异通常并不是以“非此即彼”的对立形式出现,而常常是一种“ 亦此亦彼”的中介过渡形式来表现的。比如,评价一个分校或教学点是不是很好,通常难以明确地说某个分校或教学点好,某个不好。好与不好都是模糊语言,它们之间没有明显的界限。考核评价中的许多环节,冲破了经典数学中的“要么A要么非A”的约束,经常处于一种“A与非A”的状况之中,这使考核具有极大的模糊性。
在文献[6]中,作者在广播电视大学量化考核法中使用一级模糊综合评判方法,但随着考核对象、考核指标的复杂,本文引入二级模糊综合评判方法,甚至于多极模糊综合评判方法,为更庞大的考核体系探讨更合理的方法。
在模糊集合理论中其最基本的核心思想就是隶属思想。隶属思想使我们可以对一大类不确定的管理现象进行客观的量化处理,进而可以广泛地应用以模糊集合论为基础的模糊数学的理论和方法。在系统考核评价中,由于系统的描述存在着许多模糊性的概念,我们用模糊数学对人脑评价事物的思维过程进行研究和模拟,从而形成的模糊综合评判就是一种有效的综合评价方法。
本文在研究模糊理论和综合评价方法的基础上,以实际工作当中的实例,对山西电大所属分校或教学点考核评价问题进行了研究,把模糊综合评判这种量化方法应用到教学管理当中,建立二级模糊综合评价模型,为建立三级、四级等等多级模糊综合评价模型提供方法和依据。
二、二级模糊综合评判模型
两个层次的模糊综合评判模型即二级模糊综合评判模型。
1.设有n个因素构成“考核评判因素集合”,记作:
U={u1,u2,u3,…,ui,…un} ( i=1,2,…,n)
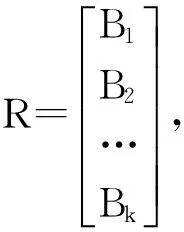
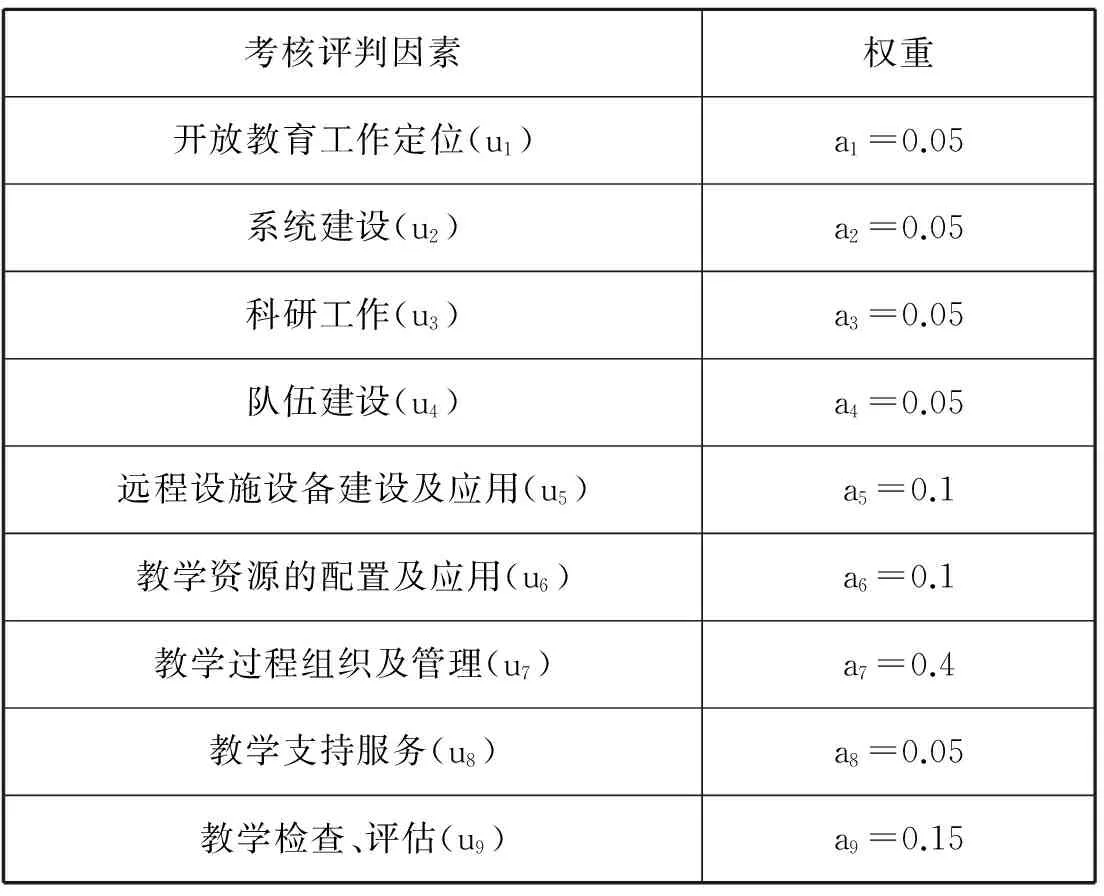
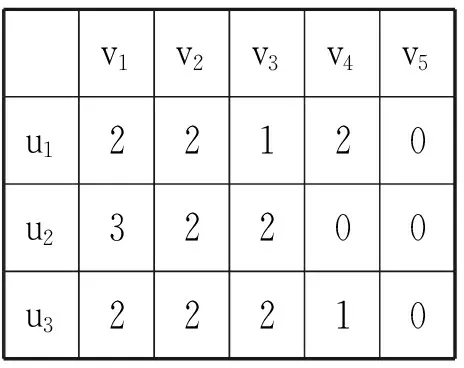
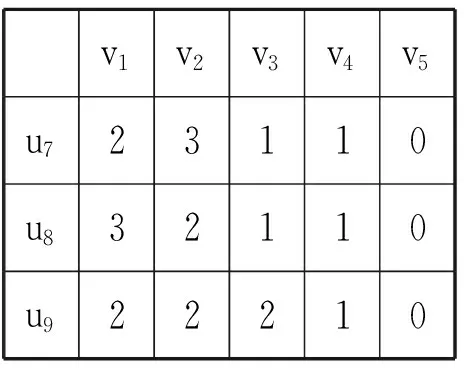
将因素集U={u1,u2,u3,…,ui,…un}分成若干组Uk(k 且Ui∩Uj=φ(i≠j)。 称U={U1,U2,…,Uk}为第一级因素集。 2.对因素 ui(i=1,2,…,n)的评判分成m种等级,全部的等级构成“考核评判等级集合”,记作: V={v1,v2,v3,…,vi,…,vm} 对第二级因素集Ui={u1(i),u2(i),…,unk(i)} 的ni个因素进行单因素评判,得单因素评判矩阵为 设Ui={u1(i),u2(i),…,unk(i)} 的权重为 求得综合评判为Ai∘ Ri=Bi(i=1,2,…,k )。 3.对第一级因素集U={U1,U2,…,Uk}做模糊综合评判。 现对山西电大所属分校或教学点考核评判为例,建立综合考核评判体系。考核体系见表1。 表1:山西电大远程教育考核体系 1.由于因素较多,权重较分散,故将因素集U={u1,u2,u3,…,u9}分为三组,即U1={u1,u2,u3},U2={u4,u5,u6},U3={u7,u8,u9},即U={U1,U2,U3}。 2.设评判集V={v1,v2,v3,v4,v5},其中,v1为优秀;v2为良好;v3为中等;v4为合格;v5为不合格。 对每个Ui(i=1,2,3)中的因素进行单因素评判,由有关专家组成评判小组,用打分或投票的办法得到相应的单因素评判集。 第一,对于第二级因素集Ui(i=1,2,3),有: Ui={u1,u2,u3} (i=1,2,3),权重A1=(0.33, 0.33, 0.33)(从表1中可以看出,a1=0.05,a2=0.05,a3=0.05,按照标准权重处理,U1中的权重均为0.33,即u1,u2,u3的权重是经过归一化处理后的结果)。建立单因素评判矩阵。考核专家组成员对被评判的对象进行评价。假定专家组成员由7人组成,用打分或投票的方法表明各自的评价。 表2 :对U1专家打分统计表 其中表2中的数字是专家们对因素 ui(i=1,2,3 )评判为vj(j=1,2,…5)的人数,我们把相应的数字放在ui所在行、vj所在列(下面计算方法相同)。 所以,单因素评判矩阵为 其中,rij的元素是表1中i行j列的人数除以7所得(下面计算方法相同)。 用模型M(∧,∨)计算得 归一化处理后得 B1=(0.28,0.24,0.24,0.24,0)。 第二,对U2={u4,u5,u6},权重经过归一化处理后,得A2=(0.2,0.4,0.4),建立单因素评判矩阵。同样由7位专家组成专家组,用打分或投票的方法表明各自的评判,得到: 表3 :对U2专家打分统计表 所以单因素评判矩阵为 做一级综合评判,得 归一化处理后得B2=(0.26,0.36,0.26,0.12,0)。 第三,对U3={u7,u8,u9},权重经过归一化处理后,得A3=(0.66,0.08,0.26),建立单因素评判矩阵。同样由7位专家组成专家组,用打分或投票的方法表明各自的评判,得到: 表4 :对U3专家打分统计表 所以单因素评判矩阵为 做一级综合评判,得 3.对第一级因素集U={U1,U2.U3} ,权重也需要进行归一化处理。从表1中可以算出 A=(0.15,0.25,0.6) 令总单因素评判矩阵为 作二级综合评判,得 B=A∘ R=(0.26,0.39,0.25,0.15,0) 此方法属于模糊综合评判的M(∧,∨)模型。该方法计算简单,但当评价因素比较多时,各权重相对较小,运算(取小)之后即ai∧rij≤rij,因此单因素评判中所得的信息rij在取小时很可能有用信息被丢失掉许多,保留的仅仅是满足rij≤ai的rij;另外一方面,当因素较少时,ai往往相应的较大,运算(取小)之后ai∧rij≤ai,因此,通过取小后一切大于rij的ai所携带的信息都会被丢掉,而影响被评价对象的主要因素总是由最大的ai来实现,这样又会失去主要因素对综合评判的影响。对于该实例,由于评价因素较多,需采用二级模糊综合评判方法来分析。因此,采取几级模糊综合评判方法需根据实际情况而定,原则上i与j相差在±1之间就比较理想。 电大系统分布在全国各地,由于地域差异、综合素质等各种原因,电大系统考核评判对象的复杂性越来越高,这种复杂性的东西是难以精确化的。如果采取传统的诸如总分法、加权平均法等评判方法,有时其评判结果很难能客观地反映事物的本质属性。此时,模糊综合评判法不失为一个比较合适的评判方法,尤其是对多元化的评判对象更是如此。二级模糊综合评判的数学模型是通过少量的信息而获得大量成果的一种评判模式。另外,此方法的应用比较成熟,足可以编制成计算机程序进行分析评判,这是本文通过实际工作实例的分析、研究和应用所要达到的目的。 : [1]Xuzhu Wang,Da Ruan,Etienne E.Kerre,Mathematics of Fuzziness-Basic Issues[M].Springer,2009. [2]刘普寅,吴孟达.模糊理论及其应用[M].长沙:国防科技大学出版社,1998. [3]谢季坚,刘承平.模糊数学方法及其应用[M].武汉:华中科技大学出版社(21世纪数学系列教材),2006. [4]梁保松,曹殿立.模糊数学及其应用[M].北京:科学出版社,2007. [5]杨红梅.模糊数学基础及应用[M].太原:山西科学技术出版社,2011. [6]杨红梅.广播电视大学量化考核法探析—引入模糊数学综合评判法及素质排队指数之我见[J].山西广播电视大学学报,2000,(4).

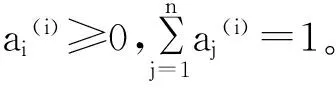

三、实例应用




四、结论
