一种鱼雷俯仰角出现±90°时的姿态仿真方法

黄华红, 杨云川, 吕艳慧



一种鱼雷俯仰角出现±90°时的姿态仿真方法

黄华红, 杨云川, 吕艳慧

(中国船舶重工集团公司第705研究所, 陕西 西安, 710075)

随着鱼雷发射平台的多样化, 火箭助飞鱼雷、空投鱼雷、自导水雷以及高空反潜鱼雷在发射和运动过程中会出现俯仰角在±90°附近的情况。当鱼雷俯仰角为±90°时, 立式三轴转台的内环轴与外环轴重合, 无法提供3个自由度的运动, 致使鱼雷姿态仿真无法进行。通过改变敏感元件安装方式, 建立在该种安装方式下三轴转台的驱动方程以及转台转角与鱼雷姿态角的转换表达式, 解决了鱼雷俯仰角出现±90°时的姿态仿真。数学仿真和半实物仿真结果表明, 该方法正确可行, 适用于鱼雷垂直发射、垂直入水以及俯仰角出现±90°时的半实物仿真试验。

鱼雷; 立式三轴转台; 俯仰角; 坐标系变换; 姿态仿真

0 引言

现代鱼雷正朝着高速度、远航程、大深度、多发射平台方向发展[1], 火箭助飞鱼雷、空投鱼雷、自导水雷以及高空反潜鱼雷在发射或者航行过程中俯仰角可能会出现±90°的情况。当鱼雷俯仰角出现±90°时, 鱼雷纵轴在海平面内的投影(′)退化为一个点, 而包含鱼雷纵轴的铅垂平面则有无穷多个, 这样就使得鱼雷偏航角和横滚角失去原有的物理意义[2]。

利用立式三轴转台进行鱼雷姿态仿真时, 敏感元件一般采用常规安装方式。在这种安装方式下, 三轴转台的3个转角分别与鱼雷空间运动的3个姿态角一一对应。这种安装方式要求鱼雷俯仰角不能超过极限值90°。由于三轴转台采用3个实体转轴串联结构, 当鱼雷俯仰角出现±90°时, 立式三轴转台的内环轴与外环轴重合, 三轴转台将失去一个自由度(在数学上称之为奇异点), 造成了模拟运动自由度的丢失, 致使鱼雷半实物仿真无法进行[3]。

垂直发射半实物仿真试验通常采用卧式三轴转台, 它克服了鱼雷俯仰角出现±90°的运动学奇异, 但会发生航向角为±90°时的运动学奇异。若要实现垂直发射方式下的助飞雷空中弹道姿态仿真, 通常采用分段仿真的方法, 即将一个完整的弹道分为两段, 分别使鱼雷处于垂直姿态和非垂直姿态, 不同的姿态模拟要求不同结构方式的三轴转台, 垂直姿态时采用卧式三轴转台, 离开垂直区域采用立式三轴转台, 这种方法的缺点是不能实现一个完整弹道的连续仿真。

本文提出了一种解决方法, 即通过改变敏感元件安装方式, 推导出在这种安装方式下的转台驱动方程和鱼雷姿态角与转台转角转换的矩阵表达式, 实现用立式转台进行鱼雷俯仰角出现±90°时的姿态仿真方法, 并对这种方法进行了理论分析、数学仿真验证以及半实物仿真应用。结果表明, 利用立式三轴转台能够实现鱼雷垂直发射、垂直入水以及俯仰角出现±90°时连续弹道的半实物仿真。

1 敏感元件安装方式

鱼雷姿态角在地面坐标系000中定义的航向角, 俯仰角, 滚动角如图1所示。

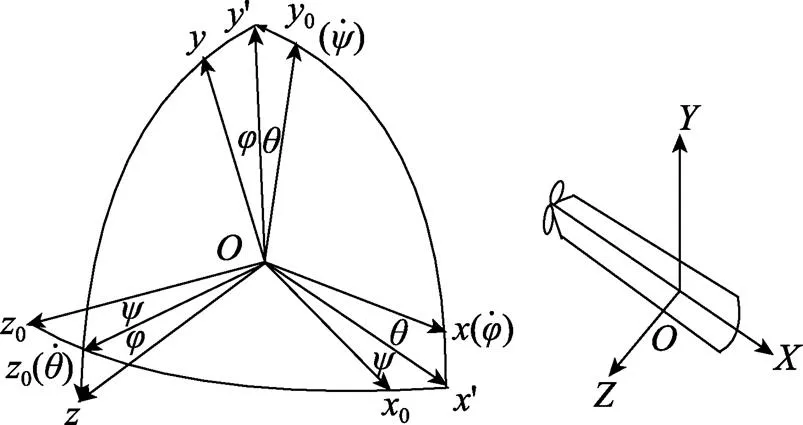
图1 鱼雷姿态角定义示意图

1.1 规安装方式

常规安装方式是将敏感元件安装在立式三轴转台的内环上, 使得鱼雷纵轴(轴)方向(简称敏感元件的纵轴)与转台内轴方向一致, 安装方式如图2(a)所示。图2中外框转角定义为, 中框转角定义为, 内框转角定义为。此时三轴转台外框、中框、内框的3个转角,,分别与鱼雷空间运动的3个姿态角,,完全一致。正因为如此, 长期以来敏感元件都采用这种安装方式。但是这种安装方式存在缺陷, 即当鱼雷俯仰角=±90°时, 立式三轴转台的内轴与外轴重合, 三轴立式转台无法模拟鱼雷绕航向轴(轴)的运动, 致使鱼雷仿真时丢失了一个自由度, 其安装示意图如图2(b)所示。

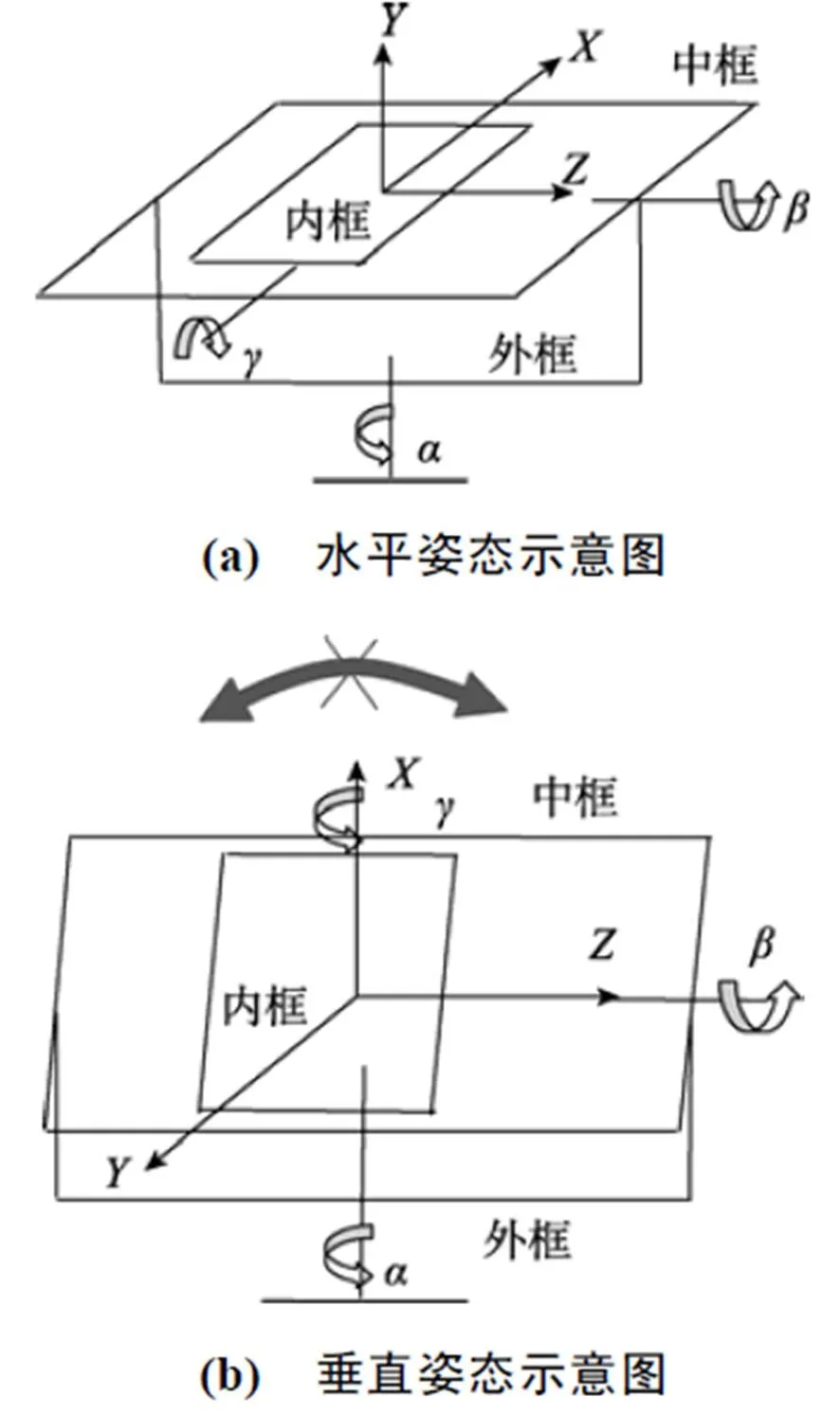
图2 常规安装方式下的姿态示意图

1.2 垂直安装方式

将常规安装方式下的敏感元件顺时针旋转90°, 安装在立式三轴转台的内框上, 即敏感元件的轴与转台内轴一致, 这种方式称为垂直安装方式, 示意图参见图3(a)。要使鱼雷处于垂直姿态, 只需在图3(a)的基础上将三轴转台内框绕轴旋转90°, 如图3(b)所示。

从图3看出, 当鱼雷处于水平姿态时, 转台外框绕鱼雷的轴转动, 中框绕鱼雷的轴转动, 内框绕鱼雷的轴转动; 当鱼雷处于垂直姿态时, 转台外框绕鱼雷的轴转动, 中框绕鱼雷的轴转动, 内框绕鱼雷的轴转动; 在这种安装方式下, 无论鱼雷处于水平姿态和垂直姿态, 均不丢失模拟运动的自由度。但是, 转台外框、中框和内框转角,,不再简单的与偏航角, 俯仰角, 滚动角相关, 因此控制三轴运动转台时, 也不能再简单地采用原有的控制量。

图3 垂直安装方式下的姿态示意图

2 三轴转台控制方案

在仿真应用中, 通常尽可能选择与鱼雷动力学方程中欧拉角旋转次序相一致的三轴转台。但是实验室的条件并不是可以任意选择的, 在具体应用时应当根据转台的型式推导其驱动方程[3]。当敏感元件在转台上的安装方式改变后, 相当于改变了欧拉角的旋转次序。下面给出了采用垂直安装方式三轴转台的驱动方程以及转台转角与鱼雷姿态角的转换关系的推导过程。

2.1 三轴转台驱动方程

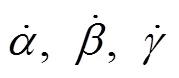
图4　 大地系与雷体系的几何关系图

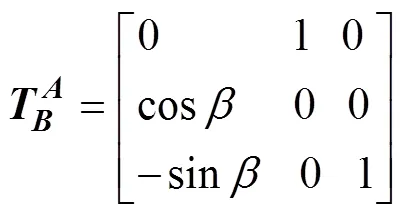
从(坐标系)转换到,,(坐标系)的转换矩阵为

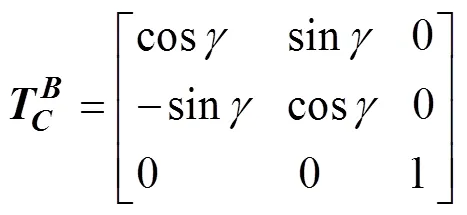
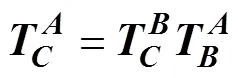
即

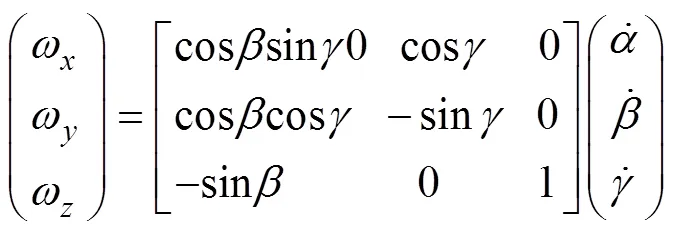
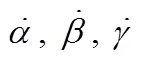
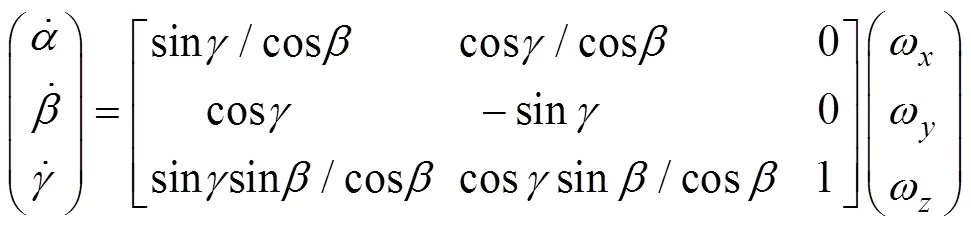
2.2 雷体姿态角与转台转角的转换方程

敏感元件采用垂直方式安装, 三轴转台转角,,与鱼雷姿态角,,的对应关系不再成立。为了建立他们之间的关系, 采用了下述法则: 即当空间某一向量从不同坐标系转换到同一坐标系, 则两者的转换矩阵对应元素应相等[4]。

从大地系向雷体系进行转换时, 欧拉角的旋转顺序为,,即先偏航, 后俯仰, 再滚动, 其转换矩阵分别为

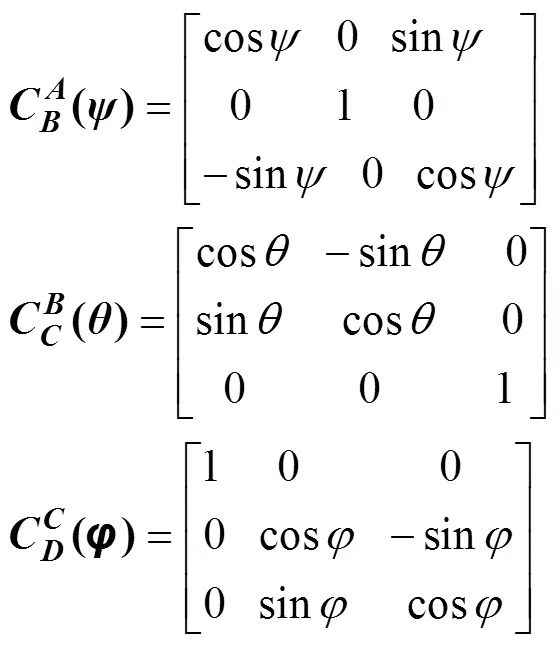
从大地系向雷体系转换矩阵为

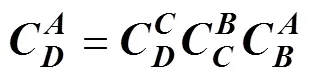
则雷体系向大地系转换表达式为式(8)。同理从大地系向转台系转换时, 按照其定义的旋转顺序, 先转转台外框转角, 再转中框转角, 后转内框转角, 其转换矩阵分别为式(9)~式(11)。

从大地系向转台系转换矩阵表达式为式(12)。从转台系向大地系的转换表达式为式(13)。

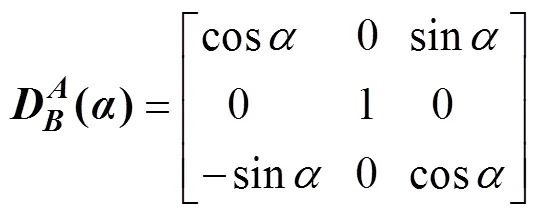
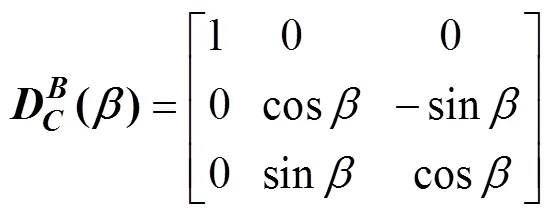
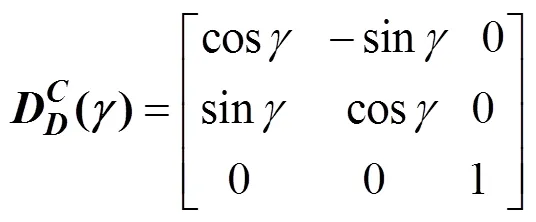
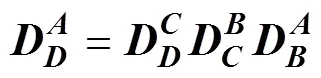
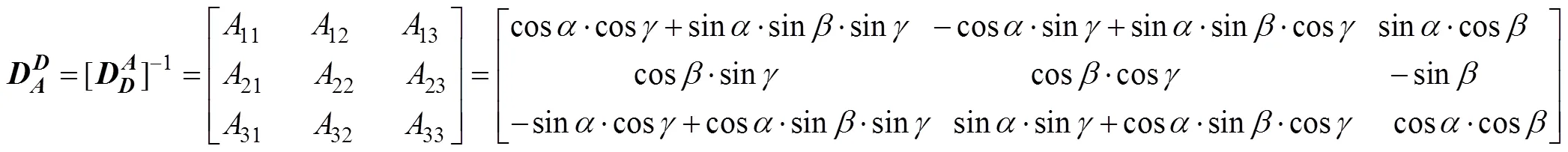
式(8)和式(13)相等, 可得

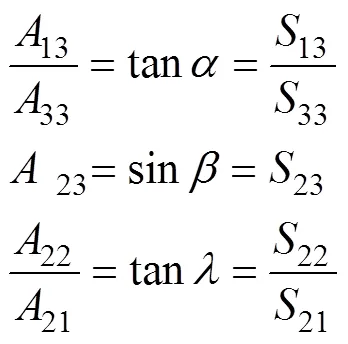
即雷体姿态角,,与三轴转台转角,,的转换表达式为式(15) ~式(17)。

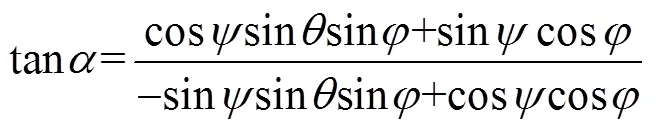
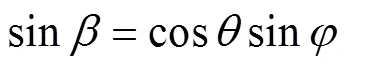
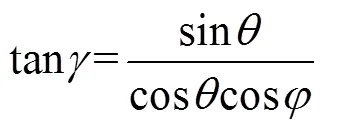
3 理论分析

以垂直发射的助飞鱼雷为例, 分析在半实物仿真过程中得到正确仿真结果的条件如下。

1) 三轴转台驱动方程在全弹道解算过程中不出现奇异点;

2) 用雷体初始姿态角计算得到的三轴转台初始转角符合实际的物理概念。

3.1 转台驱动方程奇异点分析

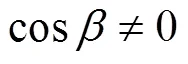
三轴转台中框转角与鱼雷的姿态角,,的关系为

图5 助飞鱼雷姿态角仿真结果

Fig. 5 Simulation results of attitude angles for rocket assisted torpedo

3.2 转台驱动方程奇异点分析

按图3方式将敏感元件安装在350转台内框的机械接口上, 俯仰角的测量范围在0°~180°, 偏航角在-360°~+360°, 横滚角在-180°~ +180°。首先比较转台转角0,0,0的物理定义是否符合鱼雷姿态角0,0,0, 其次测量的敏感元件测航姿角,,, 是否和设定的鱼雷姿态角相0,0,0一致。

已知鱼雷姿态角0,,通过转换矩阵计算出转台转角的理论值,,并作为半实物仿真试验的初始姿态。三轴转台运动到初始姿态后, 记录敏感元件的测量值,,, 并与已知的鱼雷姿态角,,进行对比, 若一致表明转换矩阵的推导是正确的。表1记录了鱼雷姿态角设定值、转台转角理论值和敏感元件实际测量值。

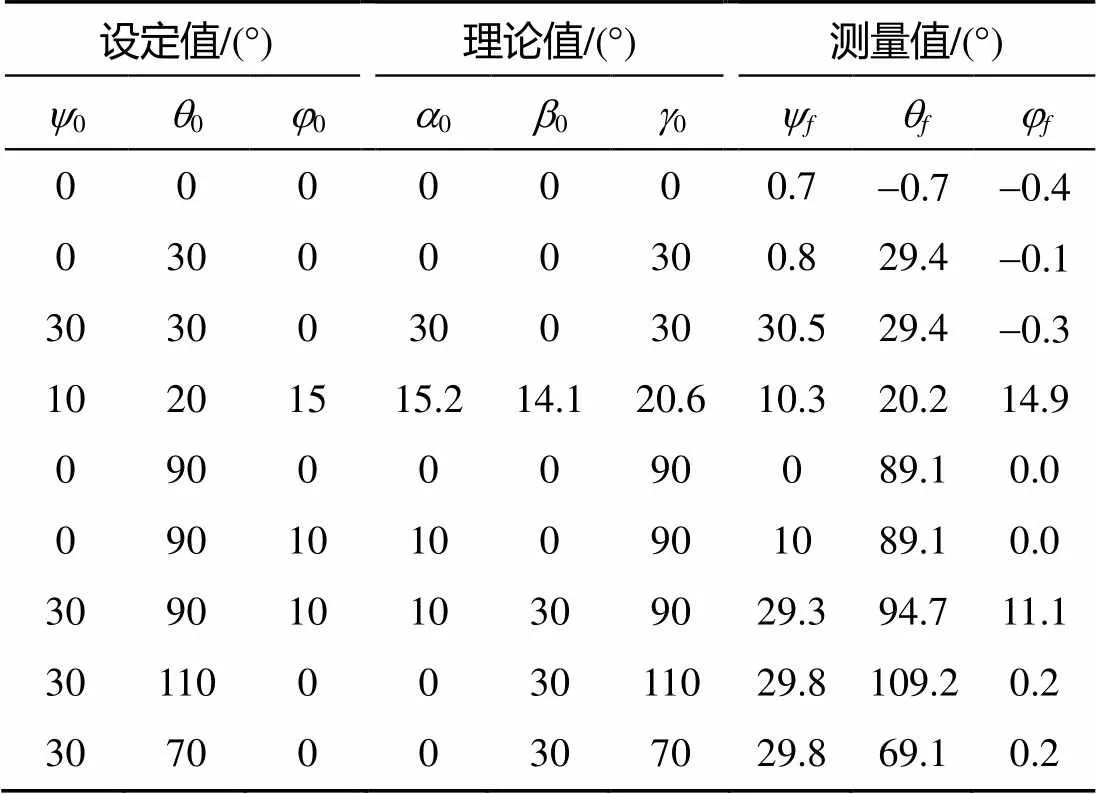
表1 鱼雷姿态角仿真数据和试验数据对照表

从表1可以看出, 无论鱼雷处于水平姿态还是垂直姿态, 航姿角误差都满足要求。

4 验证与应用

4.1 数学仿真验证

采用数学仿真方法对鱼雷姿态角与转台转角转换表达式和转台驱动方程进行验证, 数学仿真模型框图如图6所示。

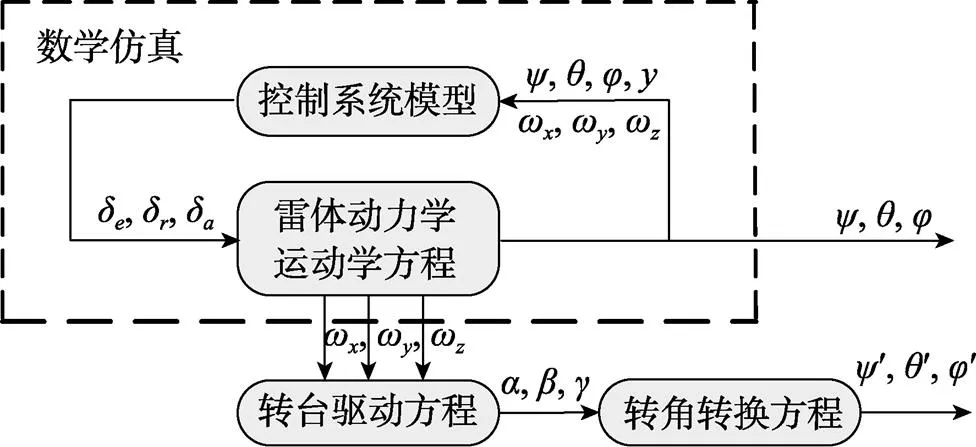
图6 数学仿真框图

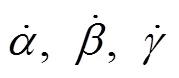
初始俯仰角90°, 射击方位角30°的标准工况数学仿真结果如图7所示。

从图7看出, 采用欧拉方程解算的雷体姿态角,,,与转台驱动方程和转换方程解算的′,′,¢重合。

4.2 半实物仿真应用

采用上述方法进行半实物仿真试验, 将雷动作为计时零点, 按风场中概率为99%的最大风进行半实物仿真, 半实物仿真的初始条件约定如下: 1) 初始弹道倾角为90°; 2) 初始弹道俯仰角为90°; 3) 发射舰艇初始方位°为0°; 4) 发射点的海拔高度为800 m; 5) 助飞雷初始速度V=18~25 m/s; 6) 助飞雷初始高度0=10~15 m; 7) 其余运动参数为缺省值。

45°侧风、45°目标方位角、射程30 km的半实物仿真试验结果参见图8。从仿真结果看出, 该工况的半实物仿真试验射击精度的纵向偏差为39 m, 横向偏差为22 m。

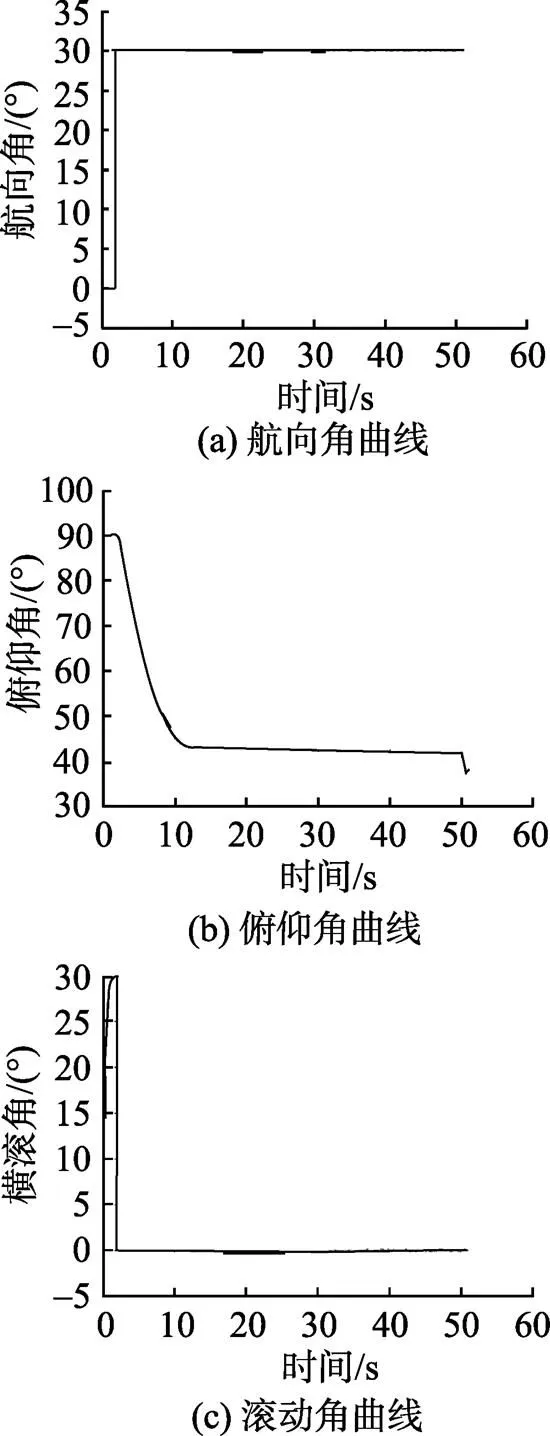
图7 鱼雷姿态角比较

5 结束语

本文针对鱼雷俯仰角出现±90°时立式三轴转台模拟自由度丢失问题, 提出了通过改变敏感元件安装方式解决立式三轴转台轴重合方案, 实现了鱼雷俯仰角出现±90°时的半实物仿真试验。这种方法的优点是经济实用, 不受实验室条件的限制, 可根据不同型号的弹道模式进行具体设计。

图8 助飞鱼雷样机半实物仿真结果

[1] 吴和声, 徐杏钦, 夏冰峰. 现代鱼雷武器的发展[J]. 军事技术, 2004, 12(4): 35-37.

[2] 李跃军, 阎超.飞行器姿态角解算的全角度双欧法[J]. 北京航空航天大学学报, 2007. 33(5): 505-508.

Li Yue-jun, Yan Chao.Improvement of Dual-Euler Method for Full Scale Eulerian Angles Solution of Aircraft [J]. Journal of Beijing University of Aeronautics and Astronautics, 2007, 33(5): 505-508.

[3] 李双勋. 防空导弹武器系统仿真[M]. 宇航出版社, 1995.

[4] 黄宣国, 空间解析几何[M]. 复旦大学出版社, 2004.

Attitude Simulation Method for Torpedo Pitch Angle at ±90º

HUANG Hua-hong, YANG Yun-chuan, LÜ Yan-hui

(The 705 Research Institute, China Shipbuilding Industry Corporation, Xi′an 710075, China)

The pitch angles of rocket assisted torpedo, airdropped torpedo, homing mine and high altitude antisubmarine torpedo will get to ±90° when they are launched and move. At this time, the inner axis and outer axis of the vertical three-axis turntable coincide with each other to lose three-degree of freedom motion, resulting in difficulty in torpedo attitude simulation. By changing the installation mode of the sensing element and establishing corresponding driving equation of the three-axis turntable and transform formula of turntable angle and torpedo attitude angle, torpedo attitude simulation is realize when torpedo pitch angle gets to ±90°. Theoretical analysis and experiment verify the correctness and feasibility of the proposed method. Simulation results show that this method can be used for semi-hardware-in-loop simulation of rocket assisted torpedo in vertical launch and water-entry, and it can also be used for many moveable objects with pitch angle ±90°.

torpedo; vertical three-axis turntable; pitch angle; coordinate conversion; attitude simulation

TJ630.33; TP391.9

A

1673-1948(2012)03-0225-06

2011-07-26;

2011-09-01.

黄华红(1966-), 女, 高级工程师, 主要研究方向为鱼雷系统仿真研究.

(责任编辑: 许 妍)