扑翼翼型流体动力特性数值计算与分析

潘 光, 钟如意, 宋保维, 曹永辉



扑翼翼型流体动力特性数值计算与分析

潘 光, 钟如意, 宋保维, 曹永辉

(西北工业大学 航海学院, 陕西 西安, 710072)

利用对海洋生物运动方式及其运动器官的研究开发水下扑翼推进装置是仿生推进技术的一个重要研究方向。本文通过数值计算方法, 以对称翼型为主, 开展对扑翼翼型的推力和升力特性的研究, 分析了各翼型在不同斯德鲁哈数下的力学表现, 以及翼型和相关参数对扑翼推进效果的影响。计算结果表明, 翼型扑翼运动时的最大推力系数、平均推力系数和最大升力系数3个参数均与中心弦长比成线性递减关系, 翼型参数和工况对翼型的推力和升力特性均有不同程度的影响。

扑翼推进; 翼型; 推力系数; 升力系数; 斯德鲁哈数; 数值计算

0 引言

近年来通过对水生生物的仿生学研究发现,海龟、海豚、企鹅以及各种鱼类等海洋生物主要依靠鳍状肢或尾翼的划水产生动力, 尽管这些生物体形不一, 但是他们却具有爆发力强、机动性高、稳定性好等共同特点。国内外学者们对此进行了大量研究, 也取得了一些仿生推进的研究成果。目前比较有代表性的有加拿大的移动机器人AQUA[1]、麻省理工学院(massachusetts institute of technology, MIT)研制的仿生扑翼水下机器人Fla- pping foil AUV[2]和机器金枪鱼RoboTuna[3]、加拿大的仿生机器海龟Madeleine[4]、美国DUKE大学的仿生扑翼水下机器人Gamera[5]、美国海军水下战中心(naval undersea warfare center, NUWC)研制的仿生扑翼水下航行器[6]等样机以及一些理论或试验研究成果。与螺旋桨推进技术相比, 水下仿生扑翼推进技术属全方向矢量推进方式, 具有机动灵活、推进噪声低、稳定性好等特点, 可在狭窄、复杂的水下环境中实现精确运动。因此, 基于对海洋生物运动方式及其运动器官的研究, 开发水下扑翼推进装置也是仿生推进技术的一个重要研究方向。

本文主要以海龟鳍状肢等的扑翼运动为研究对象, 通过数值计算, 揭示扑翼在不同翼型和运动参数下以及不同流场环境里的力学特性, 以丰富水下扑翼推进理论, 同时为扑翼航行器的研制提供理论基础。

1 翼型分析

对于海龟前肢截面形状的研究在国内外已有人进行过。文献[7]中通过采用影像剖析方法对海龟前肢进行的截面形状描绘发现, 海龟前肢截面形状近似对称, 前沿较钝, 后沿较薄, 不同截面的相对厚度和前沿半径随其离海龟肩部的距离的增大而减小, 如图1所示。而对于鱼类尾鳍, 文献[8]的研究表明, 金枪鱼尾鳍的形状在中央近似为NACA0015, 而在末端近似NACA0009。因而, 本文以对称翼型为主开展扑翼翼型对其推力和升力特性影响的研究。

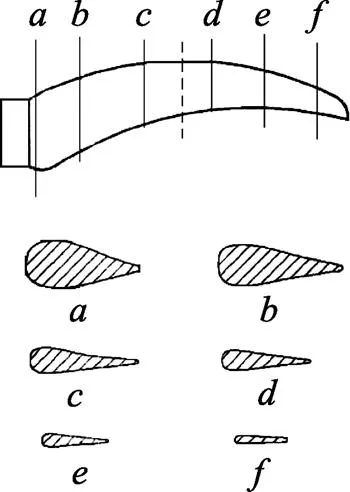
图1 海龟前肢截面形状

2 运动方程与力学分析

根据图2所示的坐标系定义, 扑翼二自由度谐振运动模型的角位移表达式为

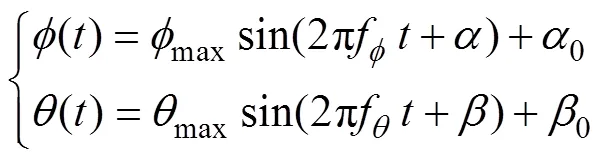
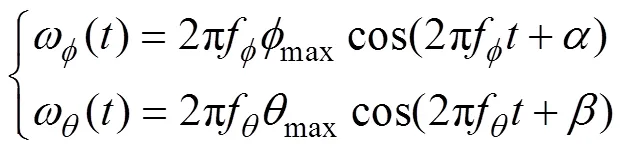
斯德鲁哈数用来定义扑翼扑动速度相对于来流速度的大小[9], 其一般表达式为

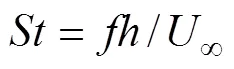
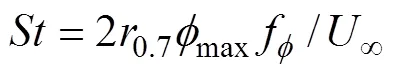
平均推力和升力分别为

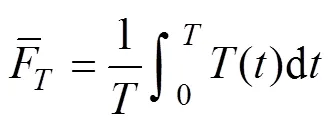
式中:()是推力方向(水平)的瞬时推力;()是升力方向(竖直)的瞬时升力;表示包括一定整数个数来回扑动所持续的时间。平均推力系数和平均升力系数的定义如下

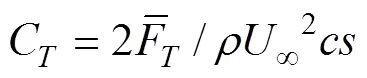
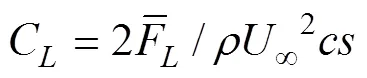
3 数值计算模型

本文基于FLUENT软件的动网格计算技术对扑翼在水中的动态运动过程进行计算, 并使用非结构化的三角形网格来进行计算域的网格划分, 为提高计算精度, 对扑翼的近壁面网格作细化, 为提高动网格的更新质量, 设置交界面以区分不同流场域。生成的初始流场网格如图3所示, 计算域尺寸为1 500 mm×800 mm, 计算条件和边界设置如表1所示。

图3 计算域网格划分和边界设置

Fig 3 Grid of computational field and boundary condi- tion

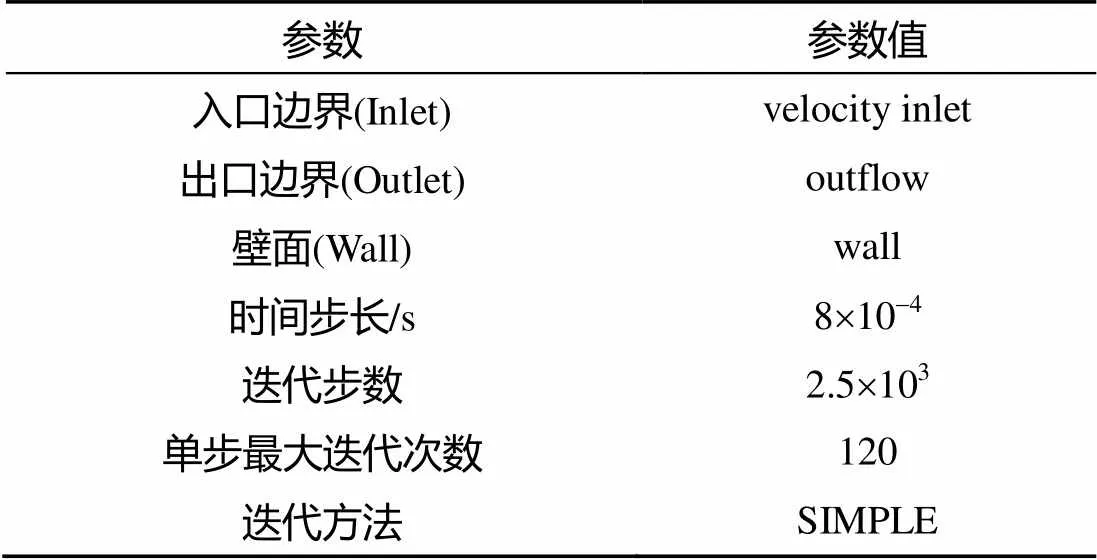
表1 边界参数与计算条件设定

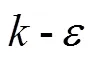
4 仿真结果与分析

4.1 运动中心位置对翼型流体动力特性的影响

扑翼在运动时, 需要绕翼板上的某点进行翻转运动和上下拍水运动, 该点的位置即为扑翼的运动中心, 如图4中的点, 它的所在位置对于扑翼的水动力特性可能存在影响。因而, 在此有必要先对此进行研究。表2为计算工况, 根据式(4)可知, 此时=0.39。

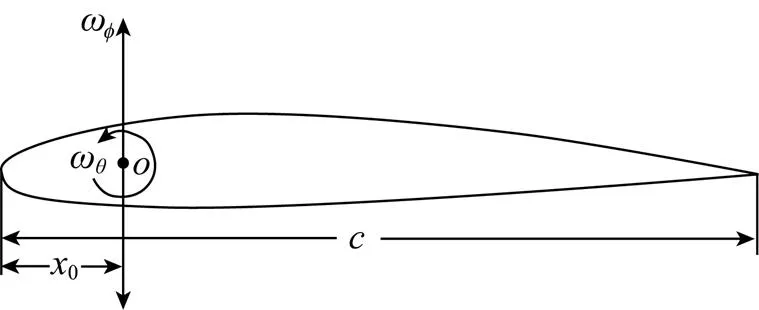
图4 扑翼运动的运动中心点示意图

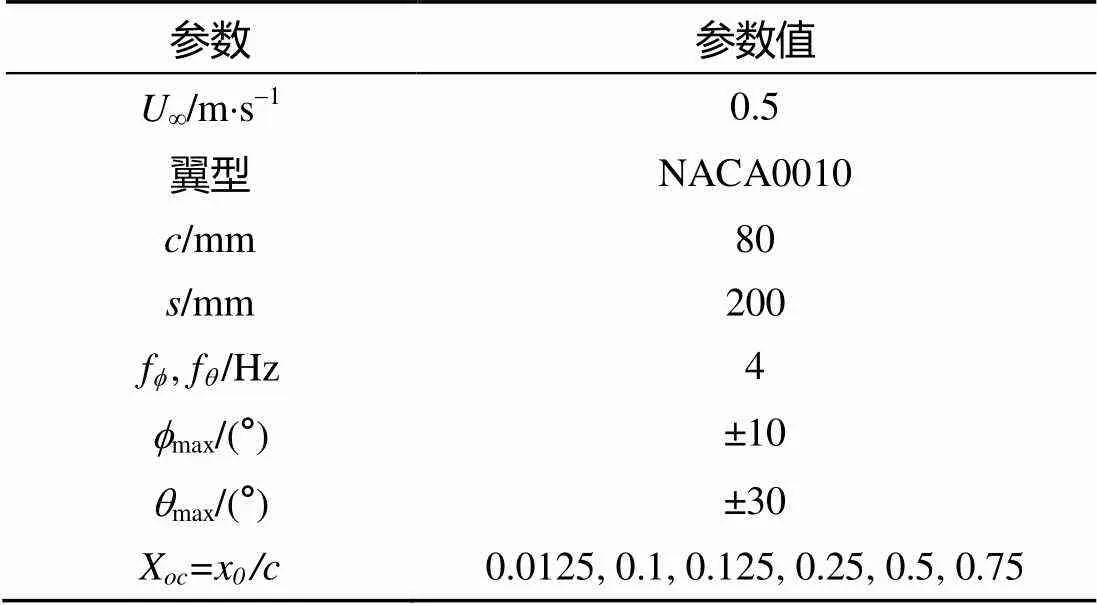
表2 计算工况

计算结果表明, 扑翼运动产生的峰值推力系数Cmax, 平均推力系数C和峰值升力系数Cmax均随X增大而下降, 平均升力系数C则无统一变化规律, 如表3所示。

对以上数据的分析和拟合后发现,Cmax,C和Cmax均与X成线性关系, 如图5所示, 其近似关系如式(9)~式(11)。

Cmax=-8.124 1 X+ 8.733 1 (9)

C=-5.778 3 X+ 4.709 8 (10)

Cmax=-12.978 7 X+ 15.476 8 (11)

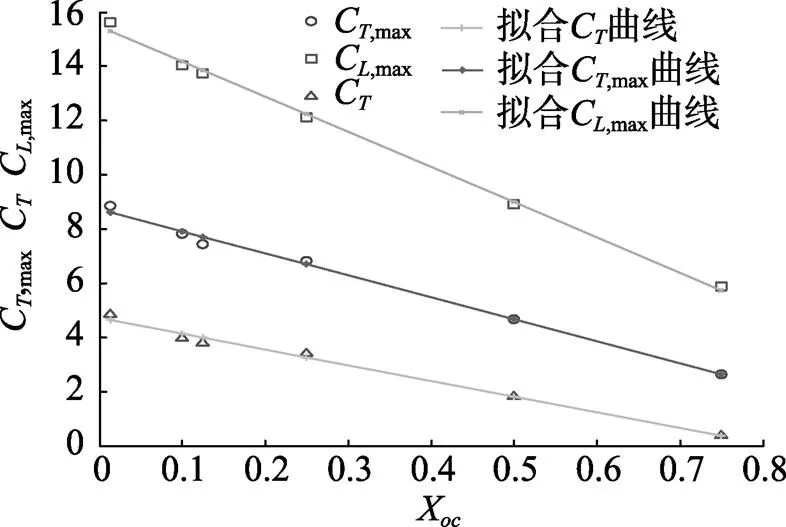
图5 峰值推力系数CT,max, 平均推力系数CT和峰值升力系数CL,max与中心弦长比Xoc的线性关系

4.2 几种翼型的扑翼水动力特性

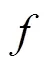
4.2.1 不同频率时各翼型扑动水动力特性

由式(4)可知, 当0.2<<0.4时, 2.1<<4.11。计算结果表明, 简谐运动驱动时各翼型扑动产生的推力和升力仍服从正弦波动规律。对不同翼型扑动产生的推力系数和升力系数进行拟合, 得到Cmax,C,Cmax和C关于的拟合曲线图, 如图6~9所示。

由图6和图7可以得到, 1) 随着的增大, 各翼型的Cmax和C均相应增大; 2) 在相同下, 同类翼型中最大厚度(以下用参数表示)越小的翼型Cmax越大, 且具有相同的对称翼型比非对称翼型Cmax更大; 3) 在较小时, 同类翼型中不同的翼型C对比没有明显的规律, 但当达到一定值时,越大的翼型C越大, 且具有相同的对称翼型和非对称翼型C差别不大。

由图8和图9可以得到, 1) 随着的增大, 各翼型的Cmax相应增大,C则没有一定规律; 2) 相同下, 同类翼型中越小的翼型Cmax越大,且具有相同的对称翼型相比非对称翼型Cmax更大; 3) 在相同下, 同类翼型基本符合越小的翼型C越大, 且具有相同的对称翼型相比非对称翼型C更大。

图6 CT,max关于扑翼参数f的变化关系

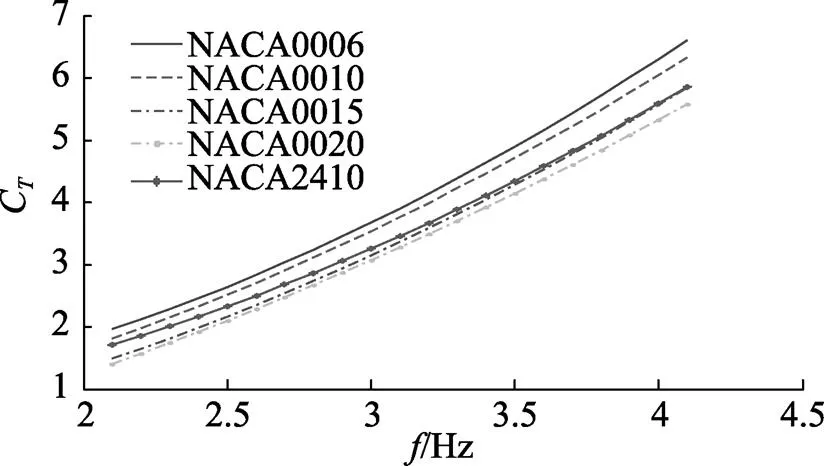
图7 CT关于f的变化关系

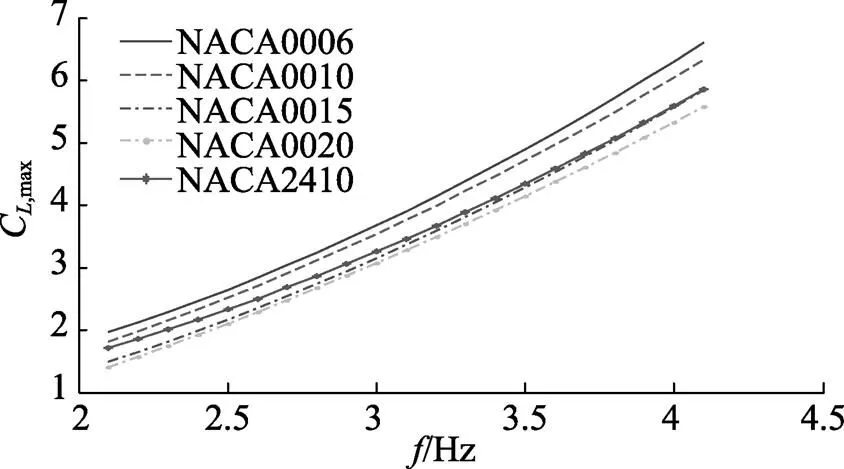
图8 CL,max关于f的变化关系

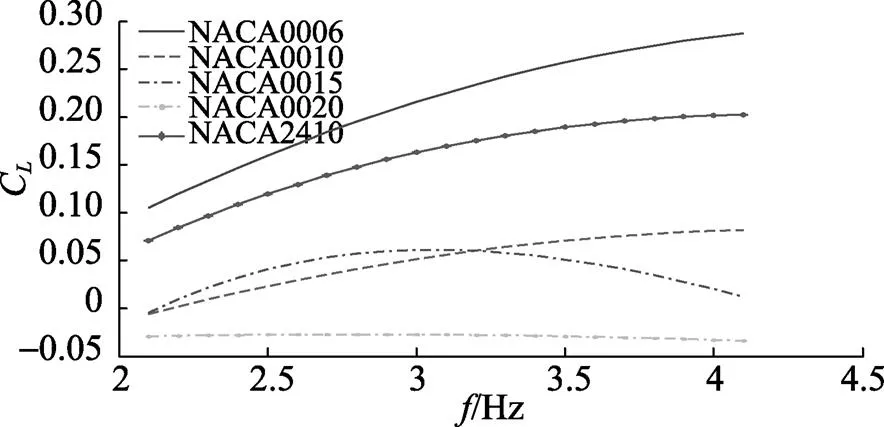
图9 平均升力系数CL关于f的变化关系

4.2.2 不同来流速度时各翼型扑动水动力特性

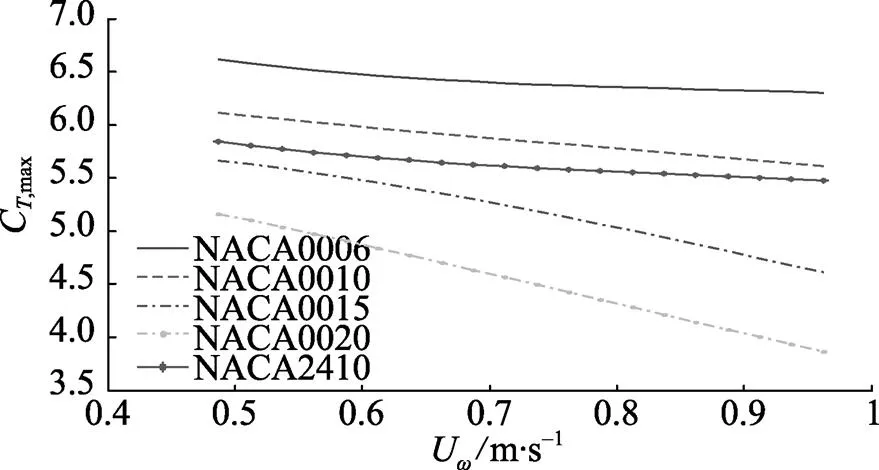
图10 CT,max关于来流速度U¥的变化关系

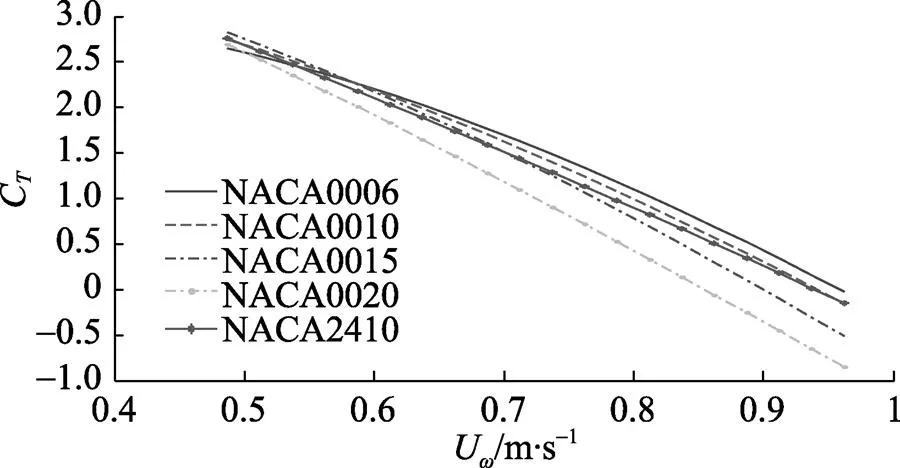
图11 CT关于U¥的变化关系

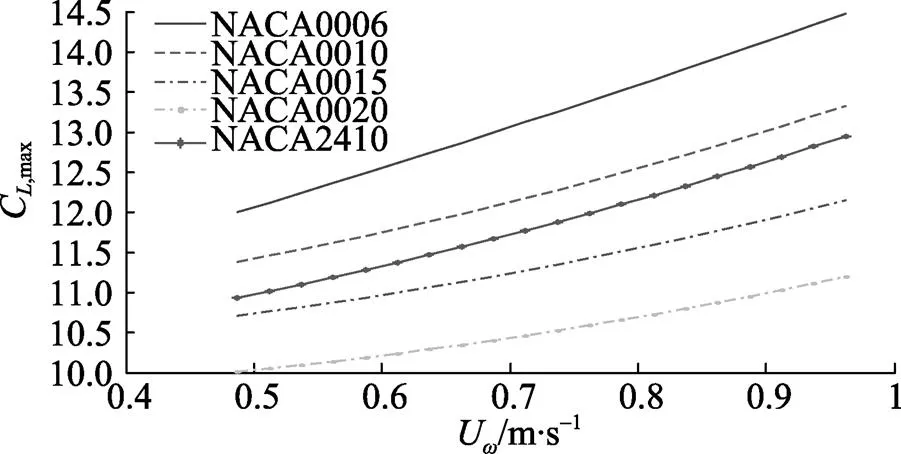
图12 CL,max关于U¥的变化关系

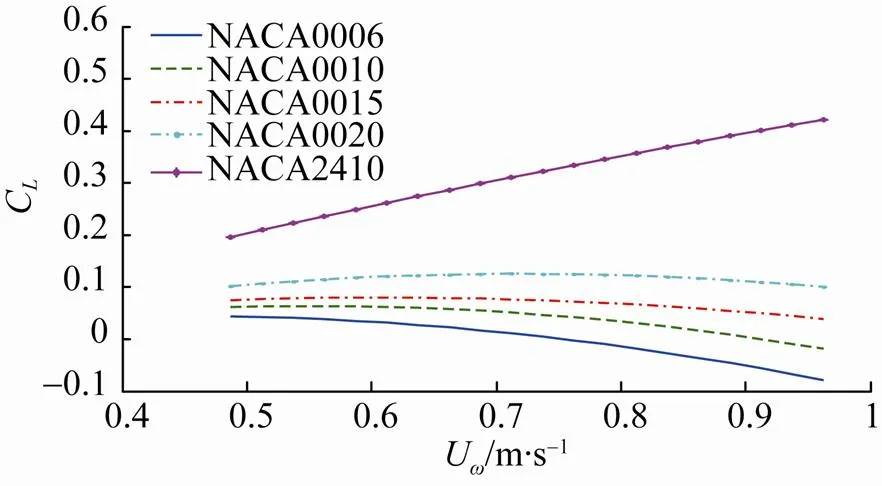
图13 CL关于U¥的变化关系

5 结论

由上述分析不难发现, 在0.2<<0.4时:

1) 翼型扑翼运动时的Cmax,C和Cmax3个参数均与中心弦长比X成线性递减关系。

[1] Dudek G, Jenkin M, Prahacs C, et al. A Visually Guided Swimming Robot[C]//2005 IEEE/RSJ International Confe- rence on Intelligent Robots and Systems: 1749-1754.

[2] Licht S, Polidoro V, Flores M, et al. Design and Projected Performance of a Flapping Foil AUV[J]. IEEE Journal of Oceanic Engineering, 2004, 29(3): 786-794.

[3] Techet A H, Hover F S, Triantafyllou M S. Separation and Turbulence Control in Biomimetic Flows[J]. Flow, Turbu- lence and Combustion, 2003, 71: 105-118, 2003.

[4] Long J H, Schumacher J, Livingston N, et al. Four Flippers or Two? Tetrapodal Swimming with an Aquatic Robot[J]. Bioinspiration & Biomimetics, 2006, 1(1): 20-29.

[5] Hsu S, Mailey C, Eade E, et al. Autonomous Control of a Horizontally Configured Undulatory Flap Propelled Vehicle [C]//2003 IEEE International Conference on Robotics & Automation: 2194-2199.

[6] Dr.Tom Swean T, Jr Office of Naval Research. ONR Unmanned Sea Vehicle Technology Development[C]//AUV SI′s Unmanned Systems Program Review. USA: 2008 Wa- shington .DC, 28th, February 2008.

[7] 刘晓白. 一种水下航行体的仿水翼法推进技术研究[D].哈尔滨: 哈尔滨工程大学, 2007: 16-17.

[8] 张晓庆, 王志东, 周林慧, 等. 三维摆动尾鳍的数值模拟[J]. 江苏科技大学学报(自然科学版), 2006, 20(1): 6-10. Zhang Xiao-qing, Wang Zhi-dong, Zhou Lin-hui, et al. Nu- merical Simulation of 3D Bionic Caudal Fin[J]. Journal of Jiangsu University of Science and Technology(Natural Science Edition), 2006, 20(1): 6-10.

[9] 梁建宏. 水下航行体仿生机理研究[M]. 北京: 北京航空航天大学出版社, 2006.

[10] Taylor G K, Nudds R L, Thomas A L R. Flying and Swimming Animals Cruise at a Strouhal Number Tuned for High Power Efficiency[J]. Nature, 2003, 425(5): 707-711.

[11] 《飞机设计手册》总编委会. 飞机设计手册第6册: 气动设计[M]. 北京: 航空工业出版社, 2002.李福海, 刘毅. 二次开发UG实现飞机操纵系统零件参数化设计与虚拟装配自动化[J]. 机械科学与技术, 2003, 22(11): 242-244.

[12] 李小力, 余世浩. 电子表单在UG软件中的应用[J]. 机械设计与制造, 2008, 4(4):62-63.

[13] B Magrab. MATLAB原理与工程应用[M].北京: 电子工业出版社, 2002.

[14] 张宇文. 鱼雷总体设计原理与方法[M]. 西安: 西北工业大学出版社, 1998.

[15] 宋保维. 水下航行器现代设计理论与方法—可靠性与优化设计[M]. 西安: 西北工业大学出版社, 2004.

[16] 王春香, 冯慧忠. MATLAB软件在机械优化设计中的应用[J]. 机械设计, 2004, 21(7): 52-54.

[17] 苏金明, 张莲花, 刘波, 等. MATLAB工具箱应用[M].北京: 电子工业s出版社, 2004.

[18] 刘惟信. 机械最优化设计[M]. (2版). 北京: 清华大学出版社, 2000.

Numerical Computation and Analysis on Hydrodynamic Characteristics of Different Profiles of Flapping Foil

PAN Guang, ZHONG Ru-yi, SONG Bao-wei, CAO Yong-hui

(College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)

This paper mainly addresses the thrust and lift characteristics of underwater symmetrical flapping foils by using the numerical computation method, analyzes the hydrodynamic of the flapping foils with different Strouhal numbers, and summarizes the influences of the profile parameters and related factors on the flapping foils′ propulsive effect. The results show that the maximal thrust coefficient, the average thrust coefficient and the maximal lift coefficient decrease linearly with increasing ratio of motion centerto chord length; the parameters of profiles and the working conditions have different effects on the thrust and lift characteristics of the foils.

flapping foil propulsion; profiles; thrust coefficient; lift coefficient; Strouhal number; numerical computation

TJ630.1; TP24

A

1673-1948(2012)01-0009-05

2011-06-24;

2011-09-07.

西北工业大学基础研究基金(G9KY1009).

潘 光(1969-), 男, 教授, 博士生导师, 主要研究方向为流体力学、水下航行器总体设计、操纵性与弹道和水下航行器特种减阻技术等.

(责任编辑: 陈 曦)