基于相似性的POLSAR占优散射归类及非监督聚类

李洪忠 陈劲松 王 超 张 红

①(中国科学院深圳先进技术研究院 深圳 518055)

②(中国科学院对地观测与数字地球科学中心 北京 100094)

1 引言

目标的极化特性与其形状结构有着本质的联系，是完整刻画目标特征不可或缺的。极化分解[1−3]将复杂的目标分解为典型散射类型加权和的形式，是实现目标极化特性提取的主要工具。文献[4]提出了一种三分量的散射分解模型，实验表明，Freeman分解对描述热带雨林的极化散射特征非常有效。文献[5]认为相比于其他方法，Freeman分解在地物分类应用中更具鲁棒性。然而，Freeman分解仍存在若干问题：(1)由于Freeman分解模型不满足旋转不变性，产生误分类；(2)当应用Freeman分解时，对某些像元，表面散射或二次散射强度为负数。

本文提出一种基于极化相似性的极化 SAR地物分类方法，将极化相似性[6]概念与 Freeman分解模型相结合。因为相似性参数具有非负性，Freeman分解时出现散射强度为负数的情况可以避免，而且相似性参数具有旋转不变性，建筑物误分类的现象得到抑制。最后以AirSAR数据进行实验，验证了该方法的有效性。

2 相关理论基础

2.1 Freeman分解

Freeman等人[4]在Van Zyl的工作基础上，建立3种散射机制的二阶极化协方差/相干矩阵模型：

(1)体散射，冠层散射体的模型是一组方位随机的细长偶极子。

(2)二次散射，其模型是一个二面角反射器。

(3)表面或单次散射，其模型是一阶布拉格表面散射体。

Freeman分解将目标相干矩阵表示为

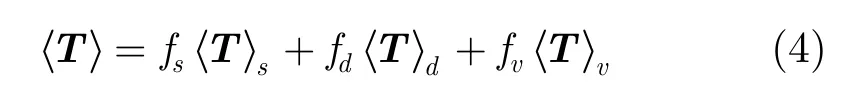
fs,fd,fv均为未知变量，分别表示三分量对散射目标的贡献。

2.2 极化相似性

Yang等人[6]定义了极化相似性参数来度量目标之间的散射相似性。

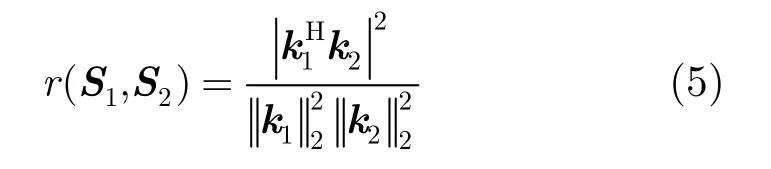
k1,k2为散射矩阵S1,S2Pauli矢量，k2表示矢量k的2-范数。极化相似性具有如下性质：

(1)旋转不变性

R(q)为旋转变换算子，q1,q2分别为S1,S2的旋转角。

(2)尺度无关性

其中a1,a2为任意非零复数。

(3)有界性

2010年，陈强等人[7,8]定义了分布式目标的二阶相干矩阵与典型目标 Pauli基矢量ki的散射相似性：

3 基于极化相似性的占优散射归类及地物分类

3.1 Freeman分解的不足

Freeman分解模型是模拟地物的散射机理建立，实验表明[4]，该分解能够准确地描述热带雨林的极化散射特征，将 Freeman分解应用到地物分类中[5]，相比于其他极化分解方法，更具鲁棒性。

然而，理论及实验结果同时表明，Freeman分解仍存在若干问题：

(1)不满足旋转不变性 不满足旋转不变性是指分解结果随目标定向角的变化而变化。定向角并非目标的固有属性，表示目标反射所引起的雷达视线方向电磁波极化方向角的变化[9]。Freeman分解中，并没有体现定向角的参数，使得同类目标分解后的结果也不同。文献[5]在将Freeman分解引入到地物分类中时，也发现目标定向角的变化会引起误分类，如建筑物朝向与雷达视线方向不对齐时，在分类结果中被归类为体散射，而不是二次散射。

近些年，去取向(Deorientation)理论被广泛的应用进行定向角的补偿[10−12]。然而定向角的变化所产生的影响主要体现在二次散射分量中，对整个目标，而不是仅仅对二次散射分量进行去取向的计算，将会产生定向角过补偿的现象，在分解结果中体现为二次散射分量过强，许多表面散射或体散射占优的地物目标被误归类为二次散射占优。

(2)散射分量强度为负数 当应用 Freeman分解到实际PolSAR数据时，对某些像元，表面散射或二次散射强度为负数，这主要是由模型求解过程引起的。Freeman分解首先确定体散射分量pv=，然后由SPAN-pv计算表面散射分量ps，二次散射分量pd, SPAN表示目标的回波强度。当，此时ps,pd为负数。此外，先求解体散射分量的计算流程容易导致表面、二次散射分量较小，使得在应用分解结果进行地物分类时，按体散射占优进行归类的植被冠层散射较实际情况明显增加。

文献[13]定义了根据植被冠层覆盖程度自适应选取的体散射模型，然而自适应选取建立在体散射模型自由度增加的前提上，增加了求解的难度。文献[10,14]通过改进Freeman分解的求解流程消除了散射分量为负数的情况，然而求解流程较复杂，且缺少实际的物理意义对应，并没有从根本上解决先确定体散射分量，再计算其他两分量的求解流程。

综上所述，Freeman分解的不足在于分解模型不满足旋转不变性以及求解过程无法保证散射分量非负性。由 2.2节，极化相似性满足旋转不变性以及有界性，因此可以通过建立极化相干矩阵与Freeman 3种散射机制模型之间的极化相似性来度量地物目标的极化散射特征，从而避免Freeman分解中所遇到的问题。

3.2 基于极化相似性的占优散射归类

为了更加准确的描述植被冠层的散射机制，本文应用文献[13,14]提出的自适应体散射模型

− 1 ≤r≤ 1 为形状参数，与植被冠层的随机散射媒质有关。r≠±1时，体散射模型秩为3，不能由单个稳态目标的散射矩阵来描述，即无法表示为典型目标的Pauli基矢量形式，式(9)的相似性无法应用，因此需要重新定义3种散射模型与目标二阶相关矩阵的极化相似性。本文应用 Cloude分解[2]的相干矩阵特征矢量分析方法将散射模型分解为3个独立的稳态相干矩阵之和：

其中li和ei分别表示特征值和特征向量，Ti均表示秩为1的独立相干矩阵，分别表示一种散射机制，其对应的li表示该散射机制的强度。将式(2)，式(3)，式(10)代入式(11)，得到

容易验证，式(12)定义的极化相似性仍然满足旋转不变性、尺度无关性以及有界性。

由式(2)，式(3)，式(10)，参数b,a,r均为未知变量，要计算极化相似性，必须进行未知参数的估计。本文依据最大似然原则建立参数估计：若表面散射占优，则由式(3)，式(4)，；若二次散射占优，则由式(2)，式(4)，；若体散射占优，则由式(4)，式(10),，参数估计如下：

上标～表示参数的估计值，函数Im, Re分别表示元素的虚部和实部。

由式(12)，式(13)可以分别建立Freeman 3种散射模型与目标相干矩阵的极化相似性，分别标记为，则认为目标以表面散射为主，以表面散射作为占优散射机制对目标进行标记；同理，当rd,rv为最大值时，分别以二次散射、体散射作为占优散射机制对目标进行标记。

3.3 Wishart最大似然分类

极化相似性满足尺度不变性，因此仅仅表示目标的极化散射特征，而与目标散射回波强度信息无关。为了综合利用目标的极化特征和回波强度信息，本文以 2维变量(D M, DP)进行目标散射的描述，DM 表示占优散射机制(Dominant scattering Mechanism),, DP表示占优散射强度 (Dominant scattering Power), DP=rDM·Tr a ce(T)。例如：对于某地物目标，若以表面散射为占优散射机制，

基于2维变量与Wishart分类器，分类流程如下：

(1)根据DP值将每种占优散射类别中的像元分成30个或更多具有相似像元个数的小聚类。于是，可以得到总数为90个或更多的初始聚类。

(2)计算每个聚类的平均相干矩阵。

(3)在每个类别中，根据类间 Wishart距离[5,15]进行初始类别的合并。如果两类具有最短的距离，且在同一散射类别中，那么合并这两个类别。只有占优散射类别相同的聚类才能进行类别合并以保持极化散射特征的纯度。

(4)将初始的类别合并到最终分类所需的类别个数 。

(5)计算各个聚类的期望相干矩阵作为聚类中心，所有像元只能分配给具有相同散射类别的聚类。迭代地应用Wishart分类器2到4次，即可终止聚类过程。

4 实验及结果分析

在本节中我们以美国旧金山地区 L波段AIRSAR全极化数据进行实验，图1(a)为该景数据的 Google Earth截图显示，图1(b)为 Pauli 分解效果显示。图2 为占优散射类型归类的比较效果图。图2(a)显示的为Freeman分解结果，图2(b)显示的为本文提出的极化相似性标记结果。

我们划分实验区域内4个典型区域进行两种占优散射归类的比较，在图2(a)中以A,B,C,D进行标示，其中A为海洋，D为山地，B为城镇街区，下方为金门公园，区域C也是整齐分布的城镇街区，与B所示街区区别在于两处街区建筑物的分布方向不同。B,C街区建筑物分布方向不同，使得路面与建筑之间二次散射的定向角不同，这正是 Lee等发现的由于Freeman分解方法不满足旋转不变性，目标定向角的变化而引起误分类的区域，建筑物朝向与雷达视线方向不对齐，在分类结果中被归类为体散射，而不是二次散射。相比于图2(a)，图2(b)中没有出现类似的问题，区域C仍以，二次散射为主，这是因为本文所介绍的极化相似性满足旋转不变性，从而避免了误分类的发生。

表1显示的为4个典型地物区域两种方法占优散射归类比较结果。对于A所示海洋区域，表面散射占优的像元从 88.11%增加到 99.72%，相应的体散射占优像元由11.77%减少为0.12%。平静的海面以bragg散射为主，在Freeman 3种散射机制中，表现为表面散射，而当风浪较大时，海面的粗糙度变大，使得部分散射产生较强的交叉极化响应，在应用Freeman分解时，就表现为体散射占优。本文应用的自适应体散射模型，可以根据海面的粗糙度自适应的进行体散射模型的建立，使得海面像元与体散射的相似性小于与表面散射的相似性，从而实现海面准确的占优散射归类。

对于D所示山地区域，从Google Earth上可以清晰的看出，该区域并不是连续分布的森林，还分布有大面积的草地以及裸露的山地，对于L波段成像特点，草地及裸地均应以表面散射为主，然而图3(a)中显示，Freeman分解的占优散射归类显然不够准确。与Freeman分解相比，本文方法对区域D散射类型的描述更加准确，表面散射占优像元从32.95%增加到 71.13%，而体散射占优像元则从64.72%减少为23.88%。

对于B,C所示城镇区域，Google Earth显示，具有植被冠层体散射的树木在城区所占比例较小，仅仅零星分布于街道两侧，而以表面散射为主的街道和以二次散射为主的建筑则占据了大部分区域。本文方法除消除了街区朝向不同所引起的误分类，对城镇实际散射类型的描述也更准确，两个区域表面散射与二次散射占优像元均有增加，而体散射占优像元减少。

图3为Wishart分类比较效果，图3(a)是以图2(a)为初始归类进行迭代的分类结果，图 3(b)以图2(b)为初始聚类。各类别颜色的分配依据图右侧的标签，每种颜色的深浅根据所在散射类型中类别的平均能量按亮度递增的方式分配。比较两幅图，相比于基于Freeman分解的结果，本文方法除了在散射机理描述上更加准确外，在分类的视觉效果上也更加具有层次感。

图1 实验区域显示

图2 占优散射归类

图3 分类结果

表1 典型区域占优散射归类比较(%)

5 结论

本文在充分分析Freeman分解模型的基础上，提出了一种基于极化相似性的极化 SAR地物分类方法，将极化相似性与Freeman分解模型相结合，通过比较各分解模型与目标相干矩阵的相似性确定占优散射类型以实现目标的初始归类，最后应用Wishart分类器对初始类别进行迭代以得到最终的分类结果。理论及实验均表明，本文方法解决了Freeman分解所存在的不足，而且在地物极化散射特征的描述上更加准确。

[1] 王超, 张红, 陈曦, 等. 全极化合成孔径雷达图像处理[M]. 北京: 科学出版社, 2008: 113-114.

[2] Cloude S R and Pottier E. A review of target decomposition theorems in radar polarimetry[J].IEEE Transactions on Geoscience and Remote Sensing, 1996, 34(2): 498-518.

[3] Touzi R, Boerner W M, and Lee J S. A review of polarimetry in the context of synthetic aperture radar: concepts and information extraction[J].Canadian Journal of Remote Sensing, 2004, 30(3): 380-407.

[4] Freeman A and Durden S L. A three component scattering model for polarimetric SAR data[J].IEEE Transactions on Geoscience and Remote Sensing, 1998, 36(3): 963-973.

[5] Lee J S, Grunes M R, and Pottier E. Unsupervised terrain classification preserving scattering characteristics[J].IEEE Transactions on Geoscience and Remote Sensing, 2004, 42(4):722-731.

[6] Yang J, Peng Y N, and Lin S M. Similarity between two scattering matrices[J].Electronics Letters, 2001, 37(3):193-194.

[7] 陈强, 蒋咏梅, 匡纲要. 一种度量目标散射相似性的新参数[J].信号处理, 2010, 26(3): 332-336.Chen Qiang, Jiang Yong-mei, and Kuang Gang-yao. A new parameter to measure the scattering similarity between distributed targets and canonical targets[J].Signal Processing,2010, 26(3): 332-336.

[8] Chen Q, Jiang Y M, Zhao L J,et al.. A scattering similarity based classification scheme for land applications of polarimetric SAR image[C]. Proceedings of 2010 IEEE 17th International Conference on Image Processing, Hong Kong,2010: 1361-1364.

[9] Lee J S, Schuler D L, and Ainsworth T L. On the estimation of radar polarization orientation shifts induced by terrain slopes[J].IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(1): 30-41.

[10] An W T, Cui Y, and Yang J. Three-component model-based decomposition for polarimetric SAR data[J].IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(6):2732-2739.

[11] Yamaguchi Y, Sato A, Boerner W M,et al..Four-component scattering power decomposition with rotation of coherency matrix[J].IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(6): 2251-2258.

[12] Lee J S and Ainsworth T L. The effect of orientation angle compensation on coherency matrix and polarimetric target decompositions[J].IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(1): 53-64.

[13] Freeman A. Fitting a two component scattering model to polarimetric SAR data from forests[J].IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(8): 2583-2592.

[14] An W T, Cui Y, and Yang J. Three-component decomposition for polarimetric SAR[C]. IEEE International Geoscience and Remote Sensing Symposium, Cape Town,2009: III 713-III 716.

[15] Lee J S, Hoppel K W, and Mango S A. Intensity and phase statistics of multi-look polarimetric and interferometric SAR imagery[J].IEEE Transactions on Geoscience and Remote Sensing, 1994, 32(5): 1017-1028.