尾流中双气泡声学特性的有限元分析

张 群, 王英民



尾流中双气泡声学特性的有限元分析

张 群, 王英民

(西北工业大学 航海学院, 陕西 西安, 710072)

舰船尾流的声学特性是尾流的主要特性之一, 而气泡是形成尾流声学特性的主要原因。通过对尾流单个气泡的主动声学特性分析, 建立了气泡的弹性球壳主动声反射/散射特性模型。结合对不同半径气泡声学特性及气泡在尾流中分布的分析, 建立了双气泡的结构模型。通过有限元分析模型在周期载荷作用下位移随频率的变化, 得到气泡的谐振频率, 计算双气泡在主动入射声源作用下的场点分布, 得到双气泡的主动声反射/散射特性。

舰船尾流; 双气泡; 声学特性; 有限元分析

0 引言

舰船在航行过程中会在其尾部留下一部分有特殊性质的海水, 即为舰船的尾流[1]。舰船尾流与周围海水相比具有很多独特的物理特性, 根据尾流所具有的不同的物理特性可以对尾流进行分类。声波相较于电磁波、光波等在水下具有传播速度快、传播距离远和衰减小的特点, 使得声波在水声工程领域得到了广泛的应用。舰船尾流与周围的水域相比具有独特的声学特性, 通过相关声学设备探测和检测尾流, 可以得到目标舰船的相关特性。分布在尾流中的气泡半径的大小、气泡间距等对尾流的声学特性起决定性作用。当入射声波的频率等于气泡的谐振频率时, 气泡对声波的衰减最大, 此时气泡的目标特性最强[2]。

通过分析气泡在主动入射声波作用下的反射/散射特性, 可以建立尾流中单个气泡的薄球壳结构模型[3], 根据气泡的谐振频率与气泡半径的大小、气泡所处水下的深度有关, 可以得到气泡的相关材料属性。有限元分析气泡结构模型, 可以得到单个气泡声场的计算结果, 为双气泡的有限元模型奠定了基础。

1 尾流中单气泡模型

尾流中的气泡对于入射的声波在水与空气的分界面会产生反射和散射作用, 且主要与气泡的谐振频率有关。通过对气泡的研究发现, 气泡的谐振频率主要由气泡的半径和所处水中的深度决定的。小气泡与谐振腔类似, 可以把它看作一个弹性元件, 根据其振动原理的类比电路, 可以求出在受迫振动下小气泡的谐振频率

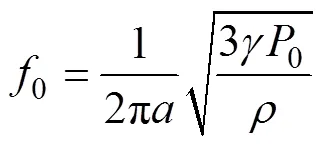
式中:为气泡半径, 单位为cm;为周围介质的密度, 尾流中的气泡处于水中, 此时周围介质的密度取=1 g/cm3;0是作用于气泡的压力, 若气泡处于水面附近, 则0=1.0´105Pa;是气体等压比热和等容比热的比值, 对于标准状态下的空气, 取空气的=1.41, 此时所得气泡谐振频率的单位为kHz。将0与气泡所处的海水深度联系起来, 则深度处的气泡的谐振频率为

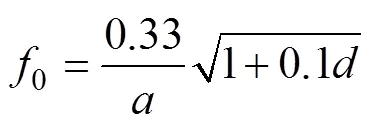
当入射声波的频率等于气泡的谐振频率时, 通过界面声波反射/散射定理, 声波可以穿透气泡壁, 并在气泡内形成多阶谐振[4], 此时气泡壁的位移最大。

以此建立尾流中单个气泡的有限元结构模型, 经过有限元计算, 得不同半径气泡的相关材料参数, 如表1 所示。

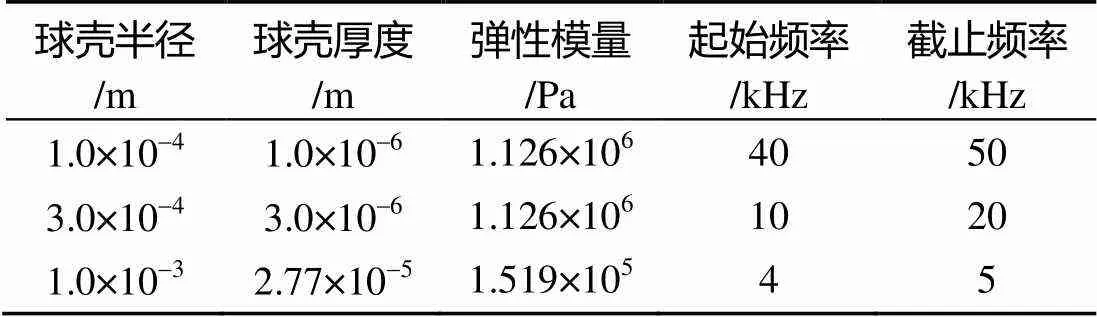
表1 有限元计算气泡相关材料参数

2 双气泡模型

尾流中气泡大小的分布与海洋背景相似[5], 气泡数密度比海洋背景中高, 且气泡之间的平均距离远大于气泡的半径。用声纳测量以15 kn航速航行的驱逐舰产生尾流气泡的分布规律, 发现尾流中直径为0.08~0.17 mm的气泡数密度达5.98×10-6kg/m3, 比周围海水的气泡数密度高1~2个数量级。利用激光全息技术研究表明, 半径在10~15μm之间, 每1μm半径宽度对应气泡数密度可达106个 /m3。

通过以上分析, 假设所取尾流模型体积为1 m3,且为正方体形状, 按气泡数密度大约为106个/m3, 将模型等分为106个小正方体, 而球壳气泡位于小正方体的中心, 则可得2个气泡中心之间的距离为2×10-2m。由此可以建立尾流中2个气泡的结构模型, 如图1所示。

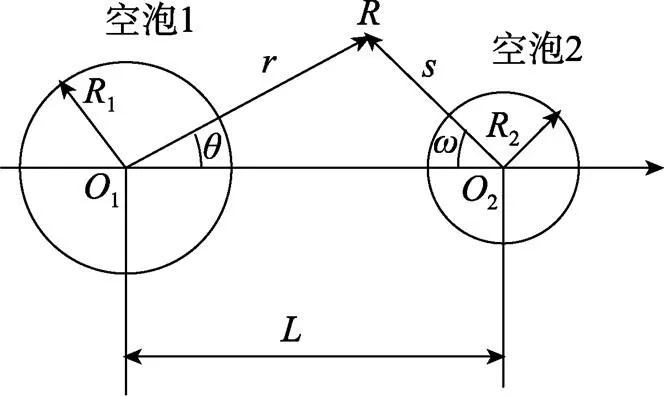
图1 双空泡球坐标

3 双气泡的有限元模型

现在利用有限元的方法来分析双气泡模型。利用ANSYS 建立双空泡的结构模型[6]。由分析可知, 两气泡之间的平均距离为2×10-2m, 可以在点1(-0.01, 0, 0)处设置局部坐标系, 建立单个尾流中气泡的薄球壳模型, 设2个气泡的半径相等, 为=1.0×10-4m, 将整个模型关于轴映射, 得到2个气泡的结构模型。为方便表示, 将2个气泡之间的距离缩短, 如图2所示。

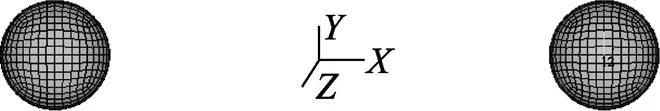
图2 双气泡结构模型

4 模型声学特性的有限元分析

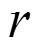
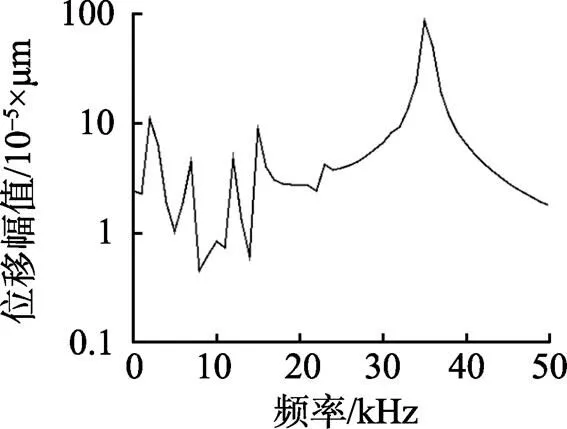
图3 r =1.0×10-4m双气泡的点在载荷下的位移变化

由图3可得点的位移最大的频率载荷, 即为该模型的谐振频率。分析结果与单个气泡的分析结果相近, 在谐振频率处, 即在=40 kHz处, 结构上点的振动位移最大。

利用间接边界元的方法, 分析2个气泡的结构模型, 在2个气泡周围建立球形场点模型, 计算频率从0~80 kHz, 间隔为1 kHz, 计算场点结构。在场点外加一离散的球形声源, 声源幅度取1, 距离场点声中心的距离为=2×10-2m, 计算场点结构, 结果如下图4所示。

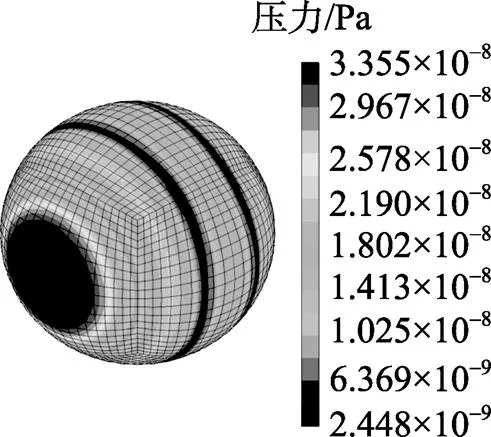
图4 40 kHz时场点计算结果

由图4示可知, 散射强度随入射频率的变化而变化, 当入射频率等于或接近气泡模型的谐振频率时, 散射最强,且按球面向外发散; 因加入了主动声源, 所以得到的声强是主动散射和主动声反射的叠加;由于主动声源的入射, 散射存在一定的方向性。与单个气泡模型的场点计算结果相比较可得: 2个气泡模型在主动入射声源的作用下, 其场点处的声强是2个气泡主动声散射和反射声强的矢量叠加, 与入射声源的位置、强度及声源与模型之间的距离有关。

若将气泡的半径取为=1.0×10-3m, 利用同样的方法分析其相关特性, 得结构模型的模态, 在模型上加入随时间变化的载荷, 结构上相应点的位移随频率的变化情况如下图5所示。

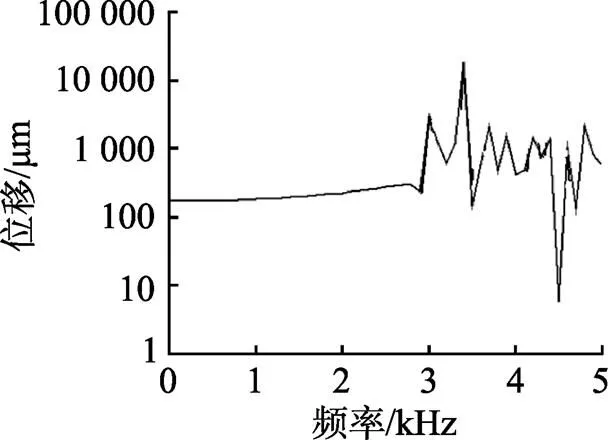
图5 r=1.0×10-3m双气泡上点在载荷下的位移变化

分析该半径的双气泡模型所得响应的位移与频率之间的曲线不是特别平滑, 但仍然可以从图中得到使模型表面位移最大的频率, 主要与结果的表示方法有关，如图6。

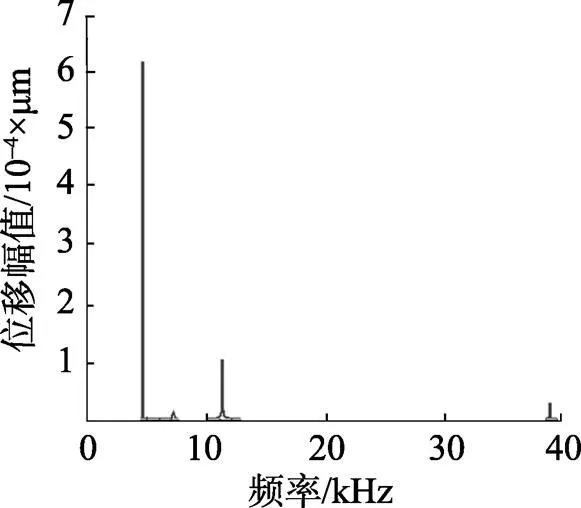
图6 r=1.0×10-3m双气泡上点在载荷下的幅度位移变化

从图6可知, 该模型对周围的一些频率点也有相应, 即相对于谐振频率为高频的模型, 该模型的谐振频率处于低频, 对附近的频率点也都很敏感。用单纯的幅度表示可以明显的得到振动位移最大处对应的谐振频率。若采用对数法表示振动位移, 并考虑对数表示中图形的连续性, 则会出现很多毛刺, 但振动位移最大处的频率不变。

比较图4和图7的场点计算结果可得: 在相同入射声强声源的作用下, 在离双气泡声中心相同位移处半径越小, 散射强度越大, 半径为1= 1.0×10-3m双气泡模型场点的散射强度为1.250 2 Pa, 而半径为2=1.0×10-4m双气泡模型场点的散射强度为3.3552Pa, 且随着半径的减小散射方向越集中, 场点强度与气泡的分布和入射声源的方向有关。若改变2个气泡之间的距离, 通过对计算结果分析可知: 随着2个气泡间距离的减小, 气泡的辐射声压增大, 分析其原因, 应为气泡之间存在相互作用, 可使气泡辐射的声强增强。

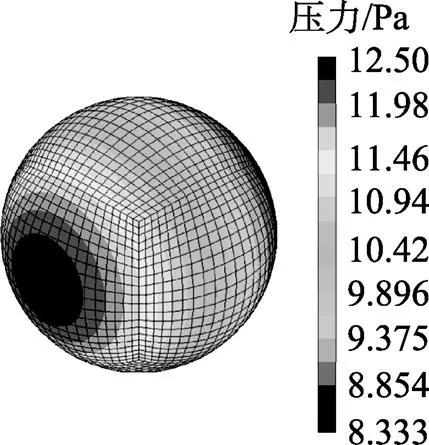
图7 4 kHz时场点计算结果

如果2个气泡的半径不同, 一个为1=1.0×10-3m, 另一个为2=1.0×10-4m, 2个气泡之间的距离仍然为=2×10-2m, 可建立2个不同半径气泡的结构模型, 将其导入SYSNOISE, 定义不同半径气泡的相关材料属性, 选择模型上特定点定义位移属性, 计算其模态, 得到模态信息。外加载荷, 计算频率范围为0~80 kHz, 间隔为1 kHz。计算结束后, 保存气泡模型上的点的位移信息, 通过函数响应,画出节点在周期载荷下的位移变化情况, 如图8所示。

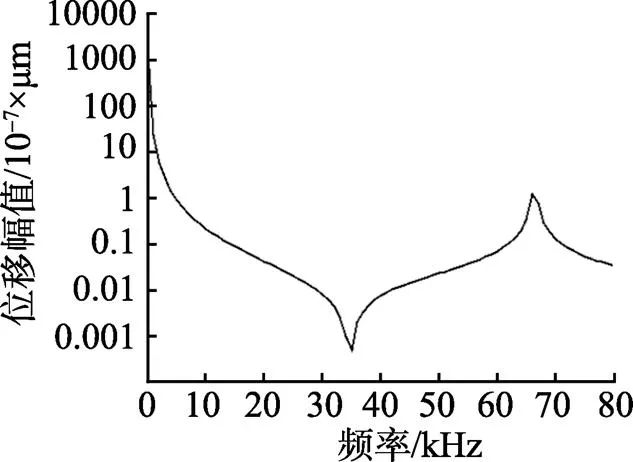
图8 不同半径气泡模型的有限元分析结果

由图示分析可知, 该模型上的点在2个频率点处都有较大的位移变化, 该模型对2个频率敏感, 即模型的谐振频率发生了变化。

建立与之对应的场点模型, 外加一个离散的单位声源并进行计算, 可得其场点的散射声强分布。若已知尾流中气泡各密度数、气泡的半径及气泡之间的距离, 根据以上结果, 结合矢量叠加及不同半径气泡之间的相互作用等方法, 可以得到尾流中气泡在主动声源入射下的主动声反射/散射强度。由于篇幅有限, 尾流中多气泡的主动声散射/反射强度及与主动声源入射强度及方位之间的关系, 后续的论文会再作研究。

5 结束语

在分析尾流中单个气泡声学特性的基础上建立了尾流中单个气泡弹性薄膜球壳的主动声学特性模型, 通过有限元计算, 得到不同半径气泡的相关材料属性。根据尾流中气泡声学特性和不同半径气泡在尾流中的分布情况, 建立双气泡的有限元结构模型, 通过对模型的有限元分析, 可以更直观的得到模型的声场分布和在外加单位离散声源作用下的场点计算结果。分析结果可得尾流中双气泡的声辐射与气泡模型的半径，气泡间的距离及主动入射声源强度和方位之间的关系。

[1] 高江, 张静远, 杨力. 舰船气泡尾流特性研究现状[J]. 舰船科学技术, 2008, 30(4): 27-32. Gao Jiang, Zhang Jing-yuan, Yang Li. The Present Situation of Research on Ship Wake Characteristic[J]. Ship Science and Technology, 2008, 30(4): 27-32.

[2] 刘伯胜, 雷家煜. 水声学原理[M]. 哈尔滨: 哈尔滨工程大学出版社, 2002: 196-199.

[3] 张群, 王英民. 舰船尾流中气泡的主动声反射/散射模型[J]电声技术, 2011, 35(8): 48-50. Zhang Qun, Wang Ying-min. Active Acoustic Reflection/ Scattering Model of the Bubble in the Ship Wake[J]. Audio Engineering, 2011, 35(8): 48-50.

[4] 李福新, 孙进才, 黄景泉. 声波激励下水中孤立气的多阶谐振[J]. 声学学报, 1996, 21(4): 475-482. LI Fu-xin, Sun Jin-cai, Huang Jing-quan. Multipole Reso- nances of an Isolated Gas Bubble in Water Excited by Sound Waves[J]. Acta Acoustic, 1996, 21(4): 475-482.

[5] 蒲中奇, 张伟, 施克仁, 等. 双空泡溃灭及空化噪声建模[J]. 清华大学学报(自然科学版), 2005, 45(11): 1450-1452. Pu Zhong-qi, Zhang Wei, Shi Ke-ren, et al. Noise Generation During the Simultaneous Collapse of Two Bubbles[J]. Tsing- hua University (Science&Technolgy), 2005, 45(11): 1450- 1452.

[6] 张朝晖. ANSYS结构分析工程应用实例与解析[M]. 3版.北京: 机械工业出版社, 2010.

[7] 李增刚. SYSNOISE Rev5.6详解[M]. 北京: 国防工业出版社, 2005.

Finite Element Analysis on Acoustic Characteristic of Double Bubble in Ship Wake

ZHANG Qun, WANG Ying-min

(College of Marine Engineering, Northwestern Polytechnical University, Xi′an 710072, China)

Acoustic characteristic, which mainly depends on bubble, is one of the most important characteristics of ship wake. In this paper, the active acoustic characteristic of single bubble in ship wake is analyzed, and an elastic sphere shell′s active acoustic reflection / scattering characteristic model of single bubble is established. A finite element model of double bubble is also set up combining the acoustic characteristic of bubble in different radius and the distribution analysis of bubbles in ship wake. Finite element analysis method is used to analyze the displacement varying with frequency under cyclic loading condition, thus the bubbles′ resonant frequencies are obtained. The distribution of double bubble field under incident active sound source is computed to obtain the active acoustic reflection / scattering characteristic of double bubble.

ship wake; double bubble; acoustic characteristic; finite element analysis

TJ630.34; O427.4; TJ631.5

A

1673-1948(2012)02-0157-04

2011-10-23;

2011-12-28.

张 群(1981-), 男, 在读博士, 研究方向为舰船尾流的主动声特性.

(责任编辑: 许 妍)