Stability Properties and Existence of Asymptotically Almost Periodic Solutions of Volterra Difference Equations*

WU Zhong-hua

(Basic Course Department，Guangzhou Nanyang College，Guangzhou 510925，China)

1 Introduction

Recently，the existence of almost periodic solutions of difference systems with delay has been treated in several works［1-7］.Y.Song and H.Tian［8］have studied the existence of periodic and almost periodic solutions for nonlinear Volterra difference equations by means of certain stability of a bounded solution.Hamaya［9］has investigated the existence of almost periodic solutions of functional difference equations with infinite delay by using stability properties of bounded solutions.Y.Xia and S.Cheng［10］have studied the existence of almost periodic solutions of ordinary difference equation by using globally quasi-uniformly asymptotically stable.In［11］，Hamaya discussed the relationships between the stability properties of solutions of the nonlinear integrodifferential equation and those in their limiting equations.In［12］，Hamaya discussed the existence of a periodic solution of an integrodifferential equation by using stability properties of a bounded solution.In this paper，we shall concern with nonlinear Volterra difference equations with unbounded delay and discuss the existence of totally stable and asymptotically almost periodic solution by using certain total stability properties of a bounded solution.

LetRmdenote Euclideanm-space，Zis the set of integers，Z+is the set of nonnegative integers andwill denote the Euclidean norm inRm，for any intervalI⊂Z:=(-∞，+∞)，we denote byBS(I)the set of all bounded functions mappingIintoRm，and

Now，for any functionx:(-∞，a)→Rmandn＜a，define a functionxn:Z-=(-∞，0］→Rmbyxn(s)=x(n+s)fors∈Z-.LetBSbe a real linear space of functions mappingZ-intoRmwith sup-norm:

We introduce an almost periodic functionf(n，x):Z×D→Rm，whereDis an open set inRm.

Definition1f(n，x)is said to be almost periodic innuniformly forx∈D，if for any ε ＞0 and any compact setKinD，there exists a positive integerL*(ε，k)such that any interval of lengthL*(ε，k)contains an integer τ

for which

for alln∈Zand allx∈K，such a number τ in above inequality is called an ε-translation number off(n，x).

In order to formulate a property of almost periodic functions，which is equivalent to the above definition，we discuss the concept of the normality of almost periodic functions.Namely，Letf(n，x)be almost periodic innuniformly forx∈D，then，for any sequence{h'k}⊂Z，there exists a subsequence{hk}of{h'k}and functiong(n，x)such that

uniformly onZ×KasK→∞，whereKis a compact set inD.There are many properties of the discrete almost periodic functions［10，13］，which are corresponding properties of the continuous almost periodic functionsf(n，x)∈C(R×D，Rm).We shall denote byT(f)the function space consisting of all translates off，that is，fτ∈T(f)，where

LetH(f)denote the uniform closure ofT(f)in the sense of(2)，H(f)is called the hull off.In particular，we denote by Ω(f)the set of all limit functionsg∈H(f)such that for some sequence{nk}，nk→∞ asK→∞ andf(n+nk，x)→g(n，x)uniformly onZ×Sfor any compact subsetSinRm.By(1)，iff:Z×D→Rmis almost periodic innuniformly forx∈D，so is a function in Ω(f).The following concept of asymptotic almost periodicity was introduced by Frechet in the case of continuous function.

Definition2u(n)is said to be asymptotically almost periodic if it is a sum of a almost periodic functionp(n)and a functionq(n)defined onI*= ［0，∞)which tends to zero asn→∞，that is，

u(n)is asymptotically almost periodic if and only if for any sequence{nk}such thatnk→∞ ask→∞ ，there exists a subsequence{nk}for whichu(n+nk)converges uniformly on 0≤n＜∞.

2 Preliminaries

We consider a system of Volterra difference equation

wheref:Z×Rm→Rmis continuous at second variablex∈RmandF(n，s，x，y)is defined forn∈Z，s∈(-∞，0］，x∈Rmandy∈Rm，and continuous forx∈Rmandy∈Rm.

We impose the following assumptions on Eq.(3):

(H1)f(n，x)is an almost periodic innuniformly forx∈Rm，andF(n，s，x，y)is almost periodic innuniformly for(s，x，y)∈k*，that is for any ε ＞0 and any compact setk*，there exists an integerL*=L*(c，k)＞0 such that any interval of lengthL*contains a τ for which

for alln∈Zand all(s，x，y)∈k*.

(H2)For any ε ＞0 and anyr＞0，there exists anS=S(ε，r)＞0 such that

for alln∈Z，whenever≤rfor all δ≤n.

(H3)Eq.(3)has a bounded solutionu(n)defined on［0，∞)which passes through(0，u0)，that is supn≥0＜∞ andu0∈BS.

LetKbe the compact set inRmsuch thatu(n)∈kfor alln∈Z，whereu(n)=φ0(n)forn≤0.

Definition3 A bounded solutionu(n)of Eq.(3)is said to be

(i)(k0，ρ)-stable(in short，(k0，ρ)-S)if for any ε ＞ 0 there exists a δ(n0，ε)＞ 0 such that ifn0≥0，ρ)＜ δ(n0，ε)，then ρ(xn，un)＜ ε for alln≥n0，wherex(n)is a solution of(3)through(n0，φ)such thatxn0(s)=φ(s)∈kfor alls≤0.

(ii)(k0，ρ)-uniformly stable(in short，(k0，ρ)-US)if for any ε ＞ 0 there exists a δ(ε)＞ 0 such that ifn0≥0，ρ()＜ δ(ε)，then ρ(xn，un)＜ ε for alln≥n0，wherex(n)is a solution of(3)through(n0，φ)such thatxn0(s)=φ(s)∈kfor alls≤0.

(iii)(k0，ρ)-equi asymptotically stable(in short，(k0，ρ)-EAS)if it is(k0，ρ)-S and for any ε ＞0，there exists a δ0(n0)＞0 and aT(n0，ε)＞0 such that ifn0≥0，ρ)＜ δ0(n0)，then ρ(xn，un)＜ ε for alln≥n0+T(ε)，wherex(n)is a solution of(3)through(n0，φ)such that(s)=φ(s)∈kfor alls≤0.

(iv)(k0，ρ)-uniformly asymptotically stable(in short，(k0，ρ)-UAS)if it is(k0，ρ)-US and is(k0，ρ)-quasi uniformly asymptotically stable，that is，if the δ0and theTin above(iii)are independent ofn0(for any ε ＞ 0 there exists a δ0＞0 and aT(ε)＞0 such that ifn0≥0，ρ()＜ δ0，then ρ(un，un)＜ ε for alln≥n0+T(ε)，wherex(n)is a solution of(3)through(n0，φ)such that(s)=φ(s)∈kfor alls≤0.).

(v)(k0，ρ)-eventually totally stable(in short，(k0，ρ)-ETS)，if for any ε ＞0，there exists a δ(ε)＞0 and α(ε)such that ifn0≥α(ε)，ρ)＜ δ(ε)andh∈BS(［n0，∞))which satisfies＜ δ(ε)，then ρ()＜ δ(ε)for alln≥n0，wherex(n)is a solution of through(n0，φ)such that(s)= φ(s)∈kfor alls≤0.If we can choose α(ε)≡0，thenu(n)is said to be(k0，ρ)-totally stable(in short，(k0，ρ)-TS).In the case whereh(n)≡0，this gives the definition of the(k0，ρ)-US ofu(n).

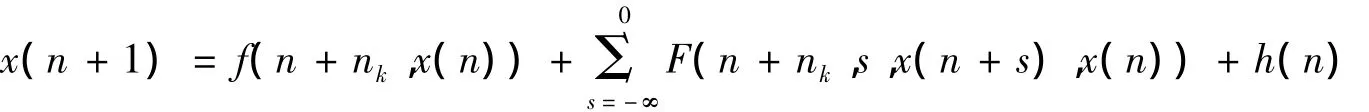
When we restrict solutionsxto those which remain ink0，that is，x(n)∈k0for alln≥n0，we say thatu(n)is relatively eventually totally(k0，ρ)-stable(in short，(k0，ρ)-RETS)and so on.

3 Main Results

Theorem1 Under the assumptions(A)through(D)，if the bounded solution u(n)of(3)is(k0，ρ)-RETS，then u(n)is asymptotically almost periodic.

ProofLet{nk}be a sequence such that nk→∞ as k→∞.If we set uk(n)=u(n+nk)，k=1，2，…，uk(n)is a solution of

and uk(n)remains in k0.Since u(n)is relatively eventually totally(k0，ρ)-stable，uk(n)is also relatively eventually totally(k0，ρ)-stable with the same(δ(·)，α(·))as for u(n).

For given ε ＞0，there exists a positive integer k1(ε)such that nk≥α(ε)if k≥k1(ε).Taking a subsequence if necessary，we can assume that uk(n)converges uniformly on any compact set in(- ∞ ，0］as k→∞ .Therefore there exists a positive integer k2(ε)such that if k，m≥k2(ε)，ρ()＜δ(ε).Clearly um(n)=u(n+nm)is a solution of

and um(n)∈k0for all n∈Z，where

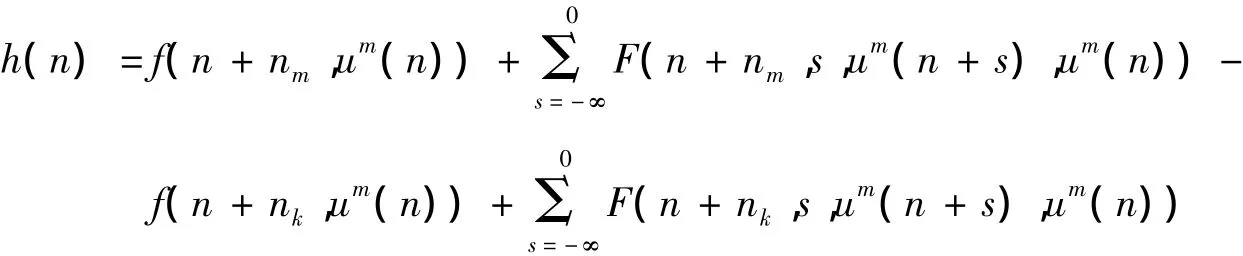
We shall show that there exists a positive integer k0(ε)such that if k，m≥k0(ε)，＜δ(ε)for n≥0，there exists a c ＞0 such that≤c for all x∈k0.It is clear that uk(n)≤c and um(n)≤c for all n∈Z.By assumption(H2)，there exists an S=S(c，ε)＞0 such that

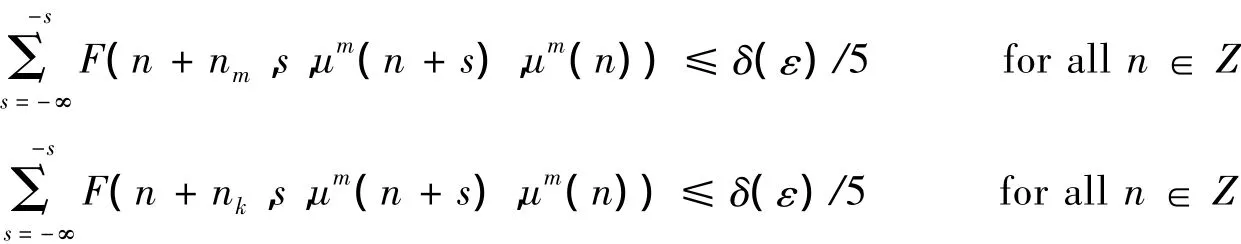
Since f(n，x)and F(n，s，x，y)are almost periodic in t for this S，there exists a positive integer k0(ε)≥max(k1(ε)，k2(ε))such that if k，m≥k0(ε).

Since we have

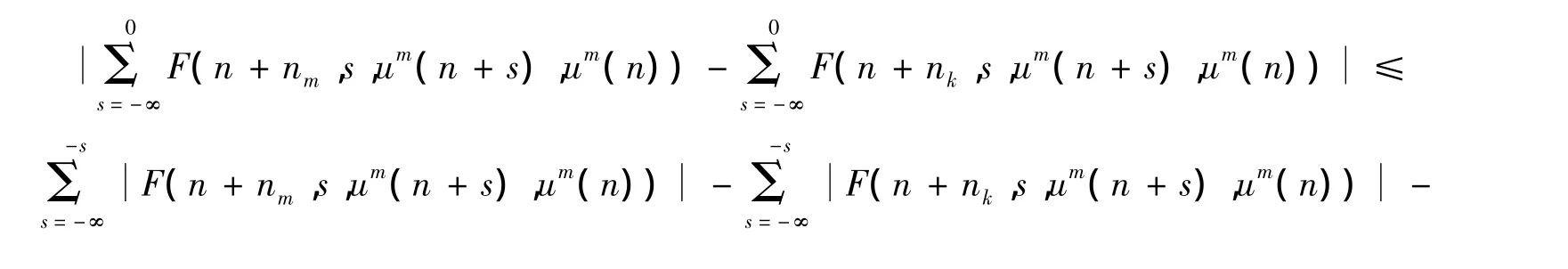
for all ε≤1/4 and all n≥0.Thus we see that for any sequence{nk}such that nk→∞ as k→∞ ，there exists a subsequence{}of{nk}for which u(n+)converges uniformly on［0，∞)as j→∞ .This shows that u(n)is asymptotically almost periodic in n.

We donte by Ω(f，F)the set of all limit functions(g(n，x)，G(n，s，x，y))such that for some sequence{nk}，nk→∞ as k→∞ ，f(n+nk，x)converges to g(n，x)uniformly on Z × S for any compact subset S in Rnand F(n+nk，s，x，y)converges to G(n，s，x，y)uniformly on Z × S*for any compact subset S*in Z*.Moreover，we denote by(v，g，G)∈Ω(u，f，F)when for the same sequence{nk}，u(n+nk)→v(n)uniformly on any compact subset in Z as k→∞.Then a system

is called a limiting equation of(3)when(g，G)∈Ω(f，F)and v(n)is a solution of(5)when(v，g，G)∈Ω(u，f，F).

In the followings，we let K be the compact set such that k=for some ε0＞ 0，wheredenotes the closure of the ε0-neighborhood N(ε0，k0)of k0.

Theorem2 Under the assumptions(A)through(D)，assume that system(3)admits a limiting equation(5)whose solution v(n)such that(v，g，G)∈Ω(u，f，F)is(k0，ρ)-TS，then u(n)is(k0，ρ)-ETS.

ProofSince(v，g，G)∈Ω(u，f，F)，there exists a sequence{nk}，nk→∞ as k→∞，such that f(n+nk，x)→g(n，s)uniformly on Z × K，F(n+nk，s，x，y)→G(n，s，x，y)uniformly on Z × S*× K × K for any compact set S*in(-∞，0］and u(n+nk)→v(n)uniformly on any compact set in Z as k→∞ .If we set uk(n)=u(n+nk)，k=1，2，…，uk(n)is a solution of

where δ(·)is the number for the total(k0，ρ)-stability of v(n).Since F(n+nk，s，x，y)→G(n，s，x，y)，we have

for the same S.Thus，by the same argument in the proof of Theorem 1，there exists a positive integer K0(ε)such that if K≥K0(ε)，

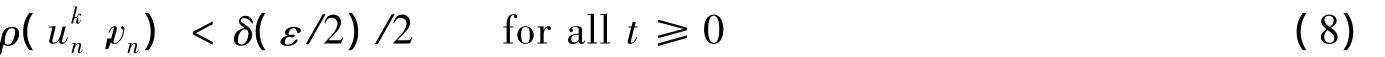
We let m=K0(ε)and α(ε)=nm.We shall show that if n0≥α(ε)，ρ()＜ δ(ε/2)/2 and＜δ(ε/2)/2 for n≥n0，where y(n)is a solution of

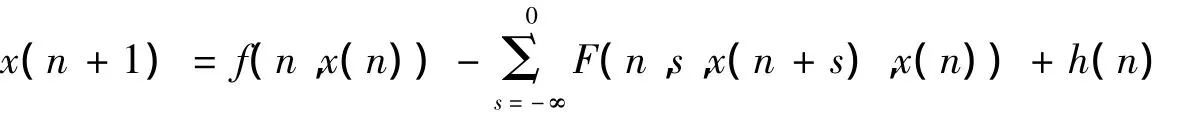
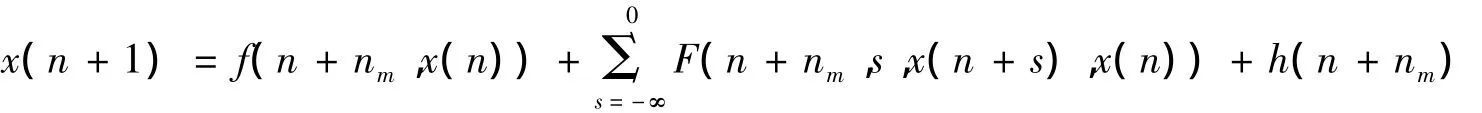
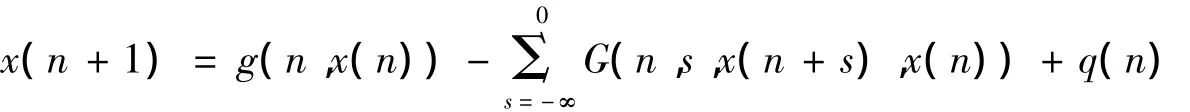
Thus the total stability of v(n)implies that ρ()＜ ε/2.

On the other hand，Eq.(8)implies that ρ(un，)＜ δ(ε/2)/2 for n≥n0.

Therefore，if n0≥α(ε)，ρ()＜ δ(ε/2)/2 and＜ δ(ε/2)/2 for n≥n0，then we have ρ(uδ，yδ)≤ρ()+ ρ()＜ ε.This contradicts ρ(uδ，yδ)= ε.Thus ρ(un，yn)＜ ε for all n≥n0，if n0≥α(ε)，ρ()＜ δ*(ε)and＜ δ*(ε)for all n≥n0，where δ*(ε)= δ(ε/2)/2.This shows that u(n)is eventually totally(k0，ρ)-stable.

［1］IGNATYEV A O，IGNATYEV O A.On the stability in periodic and almost periodic difference systems［J］.Journal of Mathematical Analysis and Applications，2006，313(2):678-688

［2］ZHANG S，LIU P，GOPALSAMY K.Almost periodic solutions of nonautonomous linear difference equations［J］.Applicable Analysis，2002，81(2):281-301

［3］AGARWAL R P，REGAN D O，WONG P J Y.On constant-sign periodic and almost periodic solutions of a system of difference equations［J］.Comput Math Appl，2005(50):1725-1754

［4］HAMAYA Y.On the existence of almost periodic solutions of a nonlinear Volterra difference equation［J］.International Journal of Difference Equations(IJDE)，2007，2(2):187-196

［5］CHOI S K，KOO N.Almost periodic solutions of nonlinear discrete Volterra equations with unbounded delay［J］.Advances in Difference Equations，2008:13-15

［6］SONG Y.Almost periodic solutions of discrete Volterra equations［J］.J Math Anal Appl，2006(314):174-194

［7］SONG Y.Periodic and almost periodic solutions of functional difference equations with finite delay［J］.Adv Differ Equ，2007:15-17

［8］SONG Y，TIAN H.Periodic and almost periodic solutions of nonlinear Volterra difference equations with unbounded delay［J］.Journal of Computational and Applied Mathematics，2007(205):859-870

［9］HAMAYA Y.Existence of an almost periodic solution in a difference equation with infinite delay［J］.J Differ Equ Appl，2003(9):227-237

［10］XIA Y，CHENG S S.Quasi-uniformly asymptotic stability and existence of almost periodic solutions of difference equations with applications in population dynamic systems［J］.Journal of Difference Equations and Applications，2008(14):59-81

［11］HAMAYA Y.Total stability property in limiting equations of integrodifferential equations［J］.Funkcial Ekvac，1990，33(2):345-362

［12］HAMAYA Y.Periodic solutions of nonlinear integrodifferential equations［J］.Tohoku Math J，1989(41):105-116

［13］CORDUNEANU C.Corduneanu.Almost periodic discrete processes［J］.Litertas Math，1982(2):159-169