小尺寸金属纳米粒子光学性质的理论研究
2012-05-25王宝娟
王宝娟
(温州大学物理与电子信息工程学院,浙江温州 325035)
小尺寸金属纳米粒子光学性质的理论研究
王宝娟
(温州大学物理与电子信息工程学院,浙江温州 325035)
半经典理论不能解析求解传导电子平均场近似势的Schrödinger方程,为了克服这种不足,用一种多台阶势近似的方法处理Woods-Saxon型势,准确地得到了能级和分段解析波函数,从而将半经典量子理论模型推广为完全的量子理论模型,并用这个模型计算了小尺寸金属纳米粒子(钠原子)表面等离子体的共振频率,结果与采用局域密度近似(LDA)方法计算的一致.
金属纳米粒子;表面等离子体;共振频率
早在罗马时代,罗马人将金属纳米颗粒掺于玻璃中,制备出名为莱克格斯(Lycurgus)杯的艺术品.该杯至今仍在大英博物馆中,当光从外面照射时,它呈现绿色,从里面照射时,却呈现红色[1].19世纪中期,Faraday[2]认为玻璃的特殊颜色可能是由掺于其中的金属纳米粒子的特殊的光学性质引起的,此后,金属纳米粒子的制备和光学性质就成了研究热点.金属纳米粒子具有异常的光学性质,在生物检测、太阳能电池、激光、纳米技术等方面具有广阔的应用前景[3-5].大量的实验研究表明,金属纳米粒子的光学性质与粒子的组成、形状、尺寸及周围的介电常数有关.本文用全量子理论的方法精确求解出传导电子平均场势的Schrödinger方程,在此基础上研究了小尺寸金属纳米粒子的光学性质.
1 金属纳米粒子光学性质的介绍
纳米粒子是粒子尺寸在1 – 100 nm之间的超细粒子.金属纳米粒子是由相对较小数量的原子组成的聚集体.从几个原子组成的团簇到超过105个原子组成的纳米粒子,一个最显著的特点是受到外场作用后,会产生一个集体的电子激发,即表面等离子体[6].图1[7]简要地表示了这一集体效应.当外加电场(其波长比纳米粒子的尺寸大得多)作用在一个金属纳米球上时,离子的质量比其中一个电子的高3个数量级,当电子离开平衡位置时,离子仍保持不动,所以金属纳米粒子表面会产生图1所示的未被抵消的电荷,由于回复力的作用,电子云在其平衡位置振荡.表面等离子体振荡就源于这个事实.虽然所有的电子围绕着正离子振荡,但产生回复力的主要影响是表面的极化.集体振荡的频率是由以下4个因素[8]决定的:电子密度、有效电子质量、电荷分布的形状和尺寸.电子的集体振荡称为粒子的偶极等离子体共振(有时称为“偶极粒子等离子体共振”,以区分出现在块状金属或金属表面的等离子体激发).

图1 金属纳米球等离子体的振荡简图
金属纳米粒子的光学性质由传导电子的集体振荡,也就是表面等离子体的元激发决定.与块体材料的等离子体集体振荡行为不同,金属纳米粒子表面等离子体的元激发可以被外部光照激发,具有异常的光学性质.在经典理论中,对光吸收光谱的理解应归功于Mie理论[9-10].该理论将体系中的粒子简化成尺寸均匀的球状粒子,且粒子与粒子相距足够远以保证粒子的散射不会相互影响.对于微小的金属粒子,电荷处于粒子的表面且无面电流分布,这要求分界面两侧的电场和磁场强度的切向分量连续而电位移矢量的垂直分量不连续.Mie理论自创立以来一直受到人们的极大重视,直到今天这个理论仍然是研究金属纳米粒子光学性质最基本的工具之一[11-12].
利用Mie的结果对绝缘介质上的一组纳米粒子进行研究,由于这种介质能很好地将聚合体分离,因此可忽略粒子间电磁场的相互作用和多重散射.球的半径远小于外加电场的波长,Mie理论给出的光吸收截面为[7]:
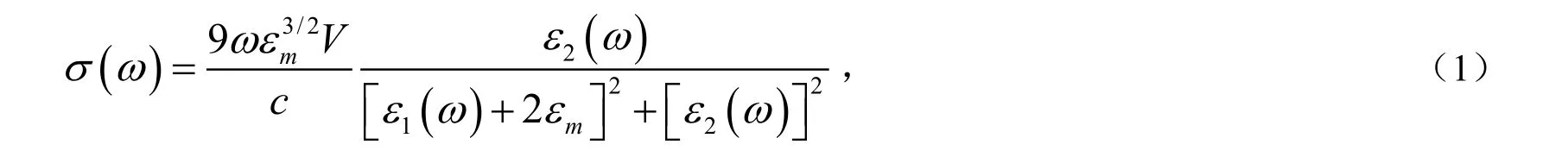
mε是插入介质的介电函①本文都采用的都是c.g.s制单位.,数(假定在光学范围内与频率是金属的复介电函数.最终得到的Mie频率
Mω为:

2 模 型
目前,国际上通常采用半经典的量子理论模型来研究球形金属纳米粒子的光学性质.“半经典”是指计算中使用了无限深势阱的半经典态密度,电子相对运动的哈密顿量只能使用平均场近似处理.对于有限大小的费米子体系,平均场近似势都是Woods-Saxon型势(如图2[13]),只能数值求解,不能解析求解传导电子平均场近似势的Schrödinger方程.本文用一种多台阶势(如图3)近似的方法处理Woods-Saxon型势,能够准确地得到能级和分段解析波函数,从而把金属纳米粒子的半经典量子理论模型推广为完全的量子理论模型.
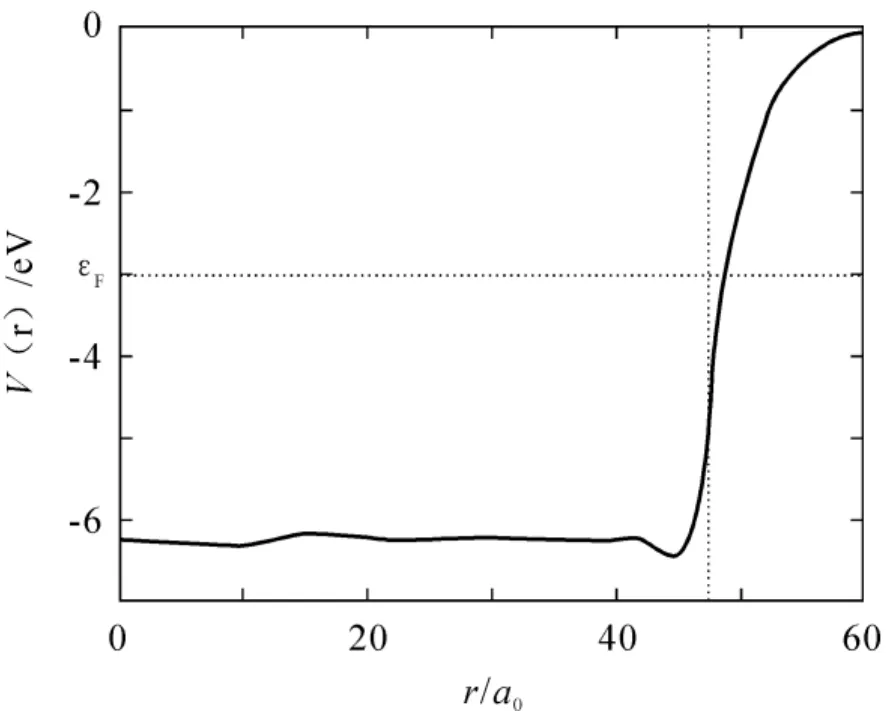
图2 钠纳米粒子的LDA自洽平均场势
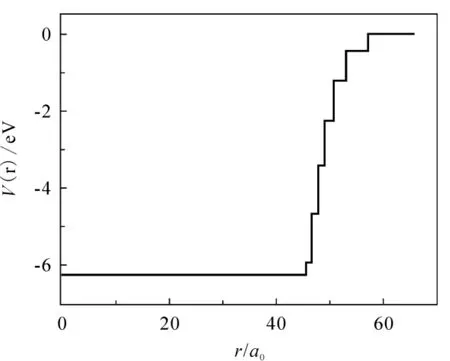
图3 多台阶势
以jellium模型为基础,电子在带正电荷、均匀分布的凝胶介质中运动,保持体系电中性.由于电子之间有长程的库仑相互作用,所以电子气在库仑力驱动下会形成某种彼此相关的集体运动.在该模型中,传导电子的哈密顿量由电子的动能、电子之间的库仑能以及正电荷背景的束缚能构成[7],即
2.1 集体坐标和相对坐标的分离
传导电子体系的哈密顿量有3个部分[14],分别描述质心运动(电子围绕离子背景振荡的体系是质心体系)、电子的相对运动能(这里是电子环境—电子与电子的相互作用或“热浴”)及它们之间的耦合作用.电子质心坐标

图4 单粒子势U与横坐标r/ a之间的关系
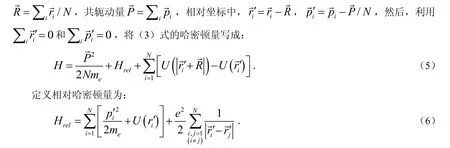
传导电子的相对运动哈密顿量构成了表面等离子体元激发的环境.传导电子的质心只能在平衡位置做微小振动,将正电荷背景对传导电子的束缚势能对其质心坐标作泰勒展开,只保留质心坐标的一次项,则传导电子的哈密顿量为:

如果传导电子的质心运动和相对运动之间没有耦合,根据Kohn定理,表面等离子体元激发与电子的相对运动及电子的数目无关,表面等离子体元激发一旦被激发出来,在无外界干扰的情况下将永远不会消失.这两部分相互耦合作用的存在导致了表面等离子体激发的耗散和退相干,使金属纳米粒子具有异常的光学性质,比如共振线宽与金属纳米粒子的大小成反比、共振峰相对于经典Mie频发生变化、金属纳米粒子附近的光场显著增强等.
2.2 平均场近似
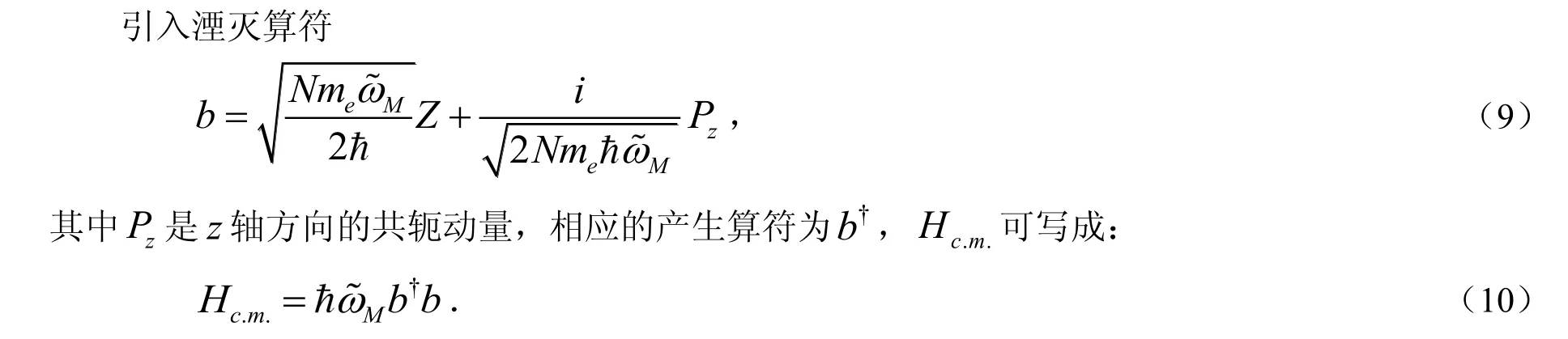
由于(9)式的哈密顿量体现了电子与电子的相互作用,用平均场近似法描绘Hrel是很有用的,可以写成:

3 溢出效应引起的频移
表面等离子体频率相对于经典的Mie值ωM出现了红移.在这一部分将计算溢出效应(影响共振频率的一个因素).用多台阶势近似的方法处理Woods-Saxon型势,在计算过程中,分别将Woods-Saxon型势(图2)依照图3的形式划分成六段和七段,但主要以七段的能级为主,我们已经准确地得到能级和分段解析波函数(通过mathematica程序来完成),从图2中可以看出,费米能级εF大约为-3.03 eV.在计算过程中,所选取的能级一部分是大于费米能级的,因此,溢出的电子数为:


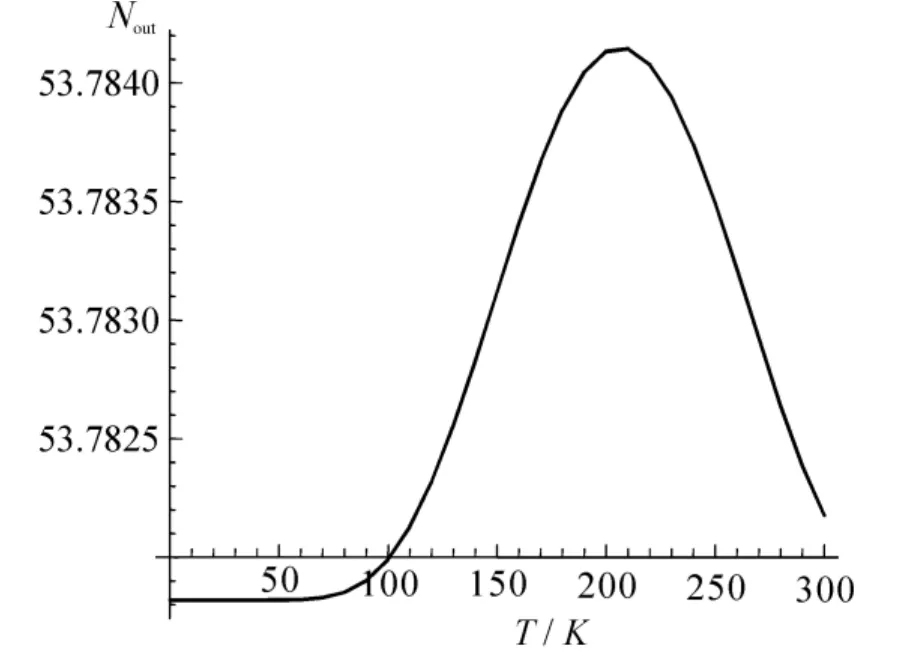
图5 溢出电子数N随温度outT变化的关系
4 环境诱发的频移
溢出效应并不能完全解释表面等离子体的红移现象,电子环境的耦合是频移的另一个来源,设环境诱发频移为δ.
1)质心从第一激发态跳到基态,产生一对电子空穴对;
2)质心从第一激发态跳到第二个激发态,一对电子空穴对湮灭;
3)质心从第一激发态跳到第二激发态,同时产生一对电子空穴对;
4)质心从第一激发态跳到基态,同时湮灭一对电子空穴对.
等离子体激发能:

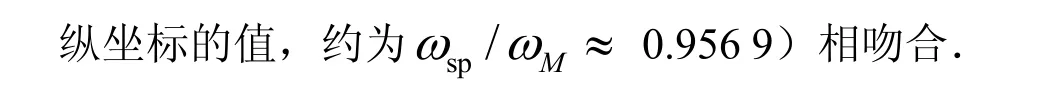
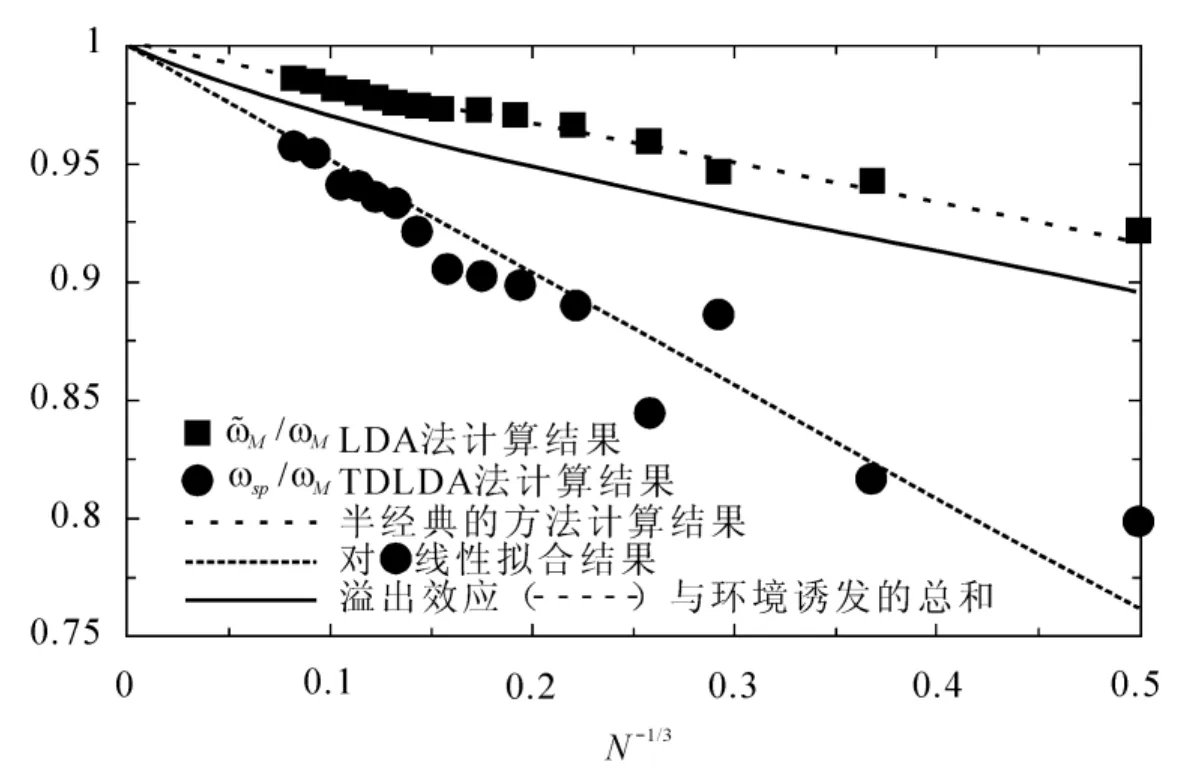
图6 表面等离子体频率与纳米粒子价电子数N的关系(N: 8 – 1 760)
5 结 论
本文提出一种多台阶势近似的方法,将半经典量子理论模型推广为完全的量子理论模型,从而精确求解了传导电子平均场近似势的Schrödinger方程.分析了金属纳米粒子中电子环境对表面等离子体共振频率的影响,通过分离相对坐标和集体坐标,说明了是粒子-空穴耦合导致了集体表面等离子体的激发频移.对于溢出效应,本文的计算结果与LDA数值计算结果一致,同时证明了电子质心坐标与相对坐标的耦合是影响表面等离子体频率红移的另一重要因素,并将其与TDLDA的数值计算结果进行比较,结果也比较吻合.
金属纳米粒子的一个重要的光学特性是具有很强的局域电磁场增强效应.纳米粒子和入射光发生表面等离子体共振时,粒子的特定部位会发生强烈的电荷集聚和振荡效应,从而在粒子的近场区域产生强烈的电磁场,称该部位为“热点”.这种电磁场增强效应能够有效地提高分子的荧光产生信号、原子的高次谐波产生效率以及分子的拉曼散射信号等,已引起各国相关研究人员的普遍关注.
[1] 周全法, 刘维桥, 尚通明. 贵金属纳米材料[M]. 北京: 化学工业出版社, 2008: 50-100.
[2] Faraday M. Experimental Relations of Gold (and Other Metals) to Light [M]. London: Philos Trans Royal Soc, 1857: 145-181.
[3] Anker J N, Hall W P, Lyandres O, et al. Biosensing with Plasmonic Nanosensors [J]. Nature Materials, 2008, 7: 442-453.
[4] Atwater H A. The Promise of Plasmonics [J]. Scientific American, 2007, 296: 56-63.
[5] Yeh D M, Huang C F, Chen C Y, et al. Surface Plasmon Coupling Effect in an InGaN/GaN Single Quantunr Well Light-emitting Diode [J]. Appl Phys Lett, 2007, DOI: 10.1063/1.2802067.
[6] Heer W A D. The physics of simple metal clusters: experimental aspects and simple models [J]. Rev Mod Phys, 1993, 65: 611-676.
[7] Kelly K L, Coronado E, Zhao L L, et al. The Optical Properties of Metal Nanoparticles: The Influence of Size, Shape, and Dielectric Environment [J]. J Phys Chem B, 2003, 107: 668-677.
[8] Jackson J B, Westcott S L, Hirsch L R, et a1. Controlling the surface enhanced Raman effect via the nanoshell geometry [J]. Appl Phys Lett, 2003, 82: 257-259.
[9] 杨志林. 金属纳米粒子的光学性质及过渡金属表面增强拉曼散射的电磁场机理研究[D]. 厦门: 厦门大学物理系, 2006: 8-150.
[10] Radloff C, Halas N J. Plasmonic Properties of Concentric Nanoshells [J]. Nano lett, 2004, 4: 1323-1327.
[11] Oubre C, Nordlander P. Finite-difference Time-domain Studies of the Optical Properties of Nanoshell Dimers [J]. J Phys Chem B, 2005, 109(20): 10042-10051.
[12] Weick G.. Quantum dissipation and decoherence of collective excitations in metallic nanoparticles [EB/OL]. [2011-06-08]. http://scd-theses.u-strasbg.fr/1153.
[13] Weick G, Ingold G L, Jalabert R A, et al. Surface plasmon in metallic nanoparticles: Renormalization effects due to electron-hole excitations [J]. Phys Rev B, 2006, DOI: 10.1103/PhysRevB.74.165421.
[14] Gerchikov L G, Guet C, Ipatov A N. Multiple plasmons and anharmonic effects in small metallic clusters [J]. Phys Rev A, 2002, DOI: 10.1103/PhysRevA.66.053202.
[15] Yannouleas C, Broglia R A. Landau damping and wall dissipation in large metal clusters [J]. Ann Phys, 1992, 217: 105-141.
Theoretical Research of Optical Property of Small Sizes Metallic Nanoparticles
WANG Baojuan
(College of Physics and Electronic Information Engineering, Wenzhou University, Wenzhou, China 325035)
Semiclassical theory couldn’t be used to analyze and solve the Schrödinger equation of conduction electron’s average field approximate potential. In order to overcome the insufficiency, an approach of a multi-step potential approximation was adopted to deal with the Woods-Saxon potential. And its accurate energy and subsection analytical wave function were then obtained. Thus, the model of semiclassical theory could be extended to a complete quantum theory model. The surface plasmon’s resonance frequency of small sizes metallic nanoparticles (sodium atom) was calculated by using this model. The result is in quantitative agreement with that achieved by local density approximation (LDA).
Metallic Nanoparticle; Surface Plasmon; Resonance Frequency
O469
A
1674-3563(2012)05-0039-08
10.3875/j.issn.1674-3563.2012.05.007 本文的PDF文件可以从xuebao.wzu.edu.cn获得
(编辑:王一芳)
2011-09-23
国家自然科学基金(KZ0911003)
王宝娟(1985- ),女,山西新绛人,硕士研究生,研究方向:金属纳米粒子的光学性质
