样本量估计及其在nQuery和SAS软件上的实现*——率的比较(一)

唐欣然 张惠风 揭著业 陈平雁

2 率的比较

2.1 单样本率的比较

2.1.1 差异性检验

2.1.1.1 单样本χ2检验

方法:Dixon ＆ Massey(1983)〔1〕根据正态近似法得到的样本量估计公式如下:

式中，α为检验水准;s取1代表单侧检验，取2代表双侧检验;1-β为检验效能;π0为已知总体率;π1为试验组预期总体率。值得注意的是，当数据来自人数有限的总体时，需对样本量的估计值进行调整，即n’=nN/(n+N)，其中n’为调整后的样本量估计值，n为通过式(1)求得的样本量估计值，N为有限总体的容量。当N与n相差较大，尤其当N值接近无限总体时，n’≈n。检验效能可由式(1)反推求得。

【例2－1】某临床试验欲验证一款彩色多普勒超声系统的临床有效性，采用标准对照设计，用图像优良率为主要评价指标，临床有效的标准为图像优良率不低于85%。预期试验机器的图像优良率为95%，以0.05为检验水准，采用双侧检验，设定检验效能为80%，试估计样本量。

nQuery Advisor 7.0实现:设定检验水准α=0.05;双侧检验，即s=2;检验效能取1-β=80% 。

在nQuery Advisor 7.0主菜单选择:

Goal:Make Conclusion Using:⊙Proportions

Number of Groups:⊙One

Analysis Method:⊙Test

方法框中选择:⊕Single proportion，One sample Chi-square。

在弹出的样本量计算窗口将各参数值键入，如图2-1所示，结果为n=79。

图2－1 nQuery Advisor 7.0关于例2-1样本量估计的参数设置与计算结果

SAS运行结果:

图2－2 SAS9.2关于例2-1样本量估计的参数设置与计算结果

2.1.1.2 单样本率确切概率检验

方法:Dixon ＆ Massey(1983)〔1〕和 Chernick ＆Liu(2002)〔2〕提出方法的基本思路为:基于累积二项分布计算检验效能，由检验效能推算样本量。首先根据检验水准α和二项分布B(n，π0)得到拒绝域，再根据拒绝域和二项分布B(n，πA)求得检验效能。其中π0为已知总体率;πA为试验组预期的总体率。

对于检验水准为α的单侧检验，H0:πA=π0，H1:πA＜π0，其拒绝域为(－∞，k)，其中k为r的最大值，k与r均为非负整数，r满足下式:

相应的检验效能计算公式如下:

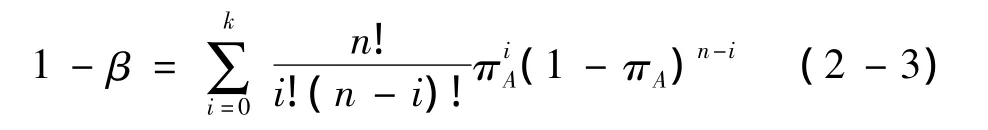
对于检验水准为α的单侧检验，H0:πA=π0，H1:πA＞π0，其拒绝域为(k，+∞)，其中k为r的最小值，k与r均为非负整数，r满足下式，

相应的检验效能计算公式如下:

对于检验水准为α的双侧检验，H0:πA=π0，H1:πA≠π0，其拒绝域为(－∞，k1)∪(k2，+∞);其中，当r满足(2－6)式时，k1为r的最大值

当r满足(2－7)式时，k2为r的最小值，

相应的检验效能计算公式如下:

【例2－2】为验证某一治疗肝癌的组合治疗方案是否有效，拟进行临床试验设计。根据以往研究数据获知，肝癌的5年生存率为50%，研究者预期新的组合治疗方案能使肝癌的5年生存率提高至60%，试按照检验效能为80%、检验水准为0.05的双侧检验估计本试验所需样本量。

nQuery Advisor 7.0实现:设定检验水准 α=0.05;双侧检验，即s=2;检验效能取1-β=80% 。在nQuery Advisor 7.0主菜单选择:

Goal:Make Conclusion Using:⊙Proportions

Number of Groups:⊙One

Analysis Method:⊙Test

方法框中选择:⊕ Single proportion，Exact test for single proportion。

在弹出的样本量估计窗口将各参数值键入，如图2－3所示，在样本量n一行反复尝试填入不同数据，直至获得检验效能达到或超过80%即为所求样本量，本例为208例。

图2－3 nQuery Advisor 7.0关于例2-2样本量估计的参数设置与计算结果

SAS9.2软件实现

图2－4 SAS9.2关于例2-2样本量估计的参数设置与计算结果

2.1.1.3 McNemar χ2检验

方法:Miettinen(1986)〔3〕针对配对设计的试验数据，给出样本量估计公式如下:

式中，η为结果不一致的对子数占总对子数的比例(不一致率)，δ为两组阳性率之差的绝对值，两个参数的具体含义见例2-3。相应的检验效能由式(2－9)反推求得。

【例2-3】为了研究服用某药是否会增加行瓣膜手术的风险，研究者设计了回顾性病例对照研究。病例组为近两年内进行过瓣膜手术的病人，按年龄、性别和体重指数将病例组与对照组配对。通过病例组和对照组填写的调查问卷来判断病人是否已服用过该药。预期对照组已服用过该药的比例为5%，病例组服用过该药的比例为10%，两组均服用过该药的比例为3%。若设定检验效能为80%，试估计该调查所需的样本量。

nQuery Advisor 7.0实现:设定检验水准 α=0.05;双侧检验，即s=2;检验效能取1-β=80% 。在nQuery Advisor 7.0主菜单选择:

Goal:Make Conclusion Using:⊙Proportions

Number of Groups:⊙One

Analysis Method:⊙Test

方法框中选择:⊕ Paired responses，paired responses:McNemar's Chi-square test。

注意，这里首先应根据各组用药比例对率差δ和不一致率η进行估计，在菜单栏中选择:

Assistants:⊙Compute Effect Size

弹出辅助计算窗口。依据上述基础数据，病例组用药比例为5%，对照组用药比例为10%，两组均服用过该药的对子数比例为3%，在弹出的计算窗口将各参数值键入，如图2-5所示，结果为δ=0.05，η=0.09。

点击Transfer后，将所计算参数传输至样本量估计窗口，如图2-6所示，结果为n=262。

图2－5 nQuery Advisor 7.0关于例2-3样本量估计中效应量的计算结果

图2－6 nQuery Advisor 7.0关于例2-3样本量估计的参数设置与计算结果

图2－7 SAS9.2关于例2-3样本量估计的参数设置与计算结果

2.1.1.4 配对设计的确切概率检验

方法:Dixon ＆ Massey(1983)〔1〕和 Chernick ＆Liu(2002)〔2〕提出方法的基本思路为:基于累积二项分布计算检验效能，由检验效能推算样本量。首先定义样本量为n，结果不一致的对子数为m，由2.1.1.3的参数η和δ的解释可知m～B(n，η)，故可根据二项分布概率密度公式求得每个m值对应的概率p(m)。然后，可参考2.1.1.2的方法算出每个m值对应的检验效能power(m):由检验水准α和二项分布B(m，0.5)得到拒绝域，再根据拒绝域和二项分布B(m，(1/2)(1+δ/η))求得每个m值对应的检验效能。最后，以p(m)做权重，对每个m值的检验效能求和，即得到最终所求检验效能(对于检验效能小于10－7的m值忽略不计)，计算公式如下:

式中m0、m1满足 p(m ＜ m0)≤10－7，p(m ＞ m1)≥10－7。

【例2-4】以例2-3为例，已知服药不一致的对子数比例为9%(见图2-5中“Proportion discordant，η”一栏)，病例组与对照组的服药率差值为5%，对该研究做配对设计的确切概率检验，试估计检验效能为80%时的样本量。

nQuery Advisor 7.0实现:设定检验水准 α=0.05;双侧检验，即 s=2;δ=0.05，η =0.09。

在nQuery Advisor 7.0主菜单选择:

方法框中选择:⊕ Paired responses，paired responses:exact sign test。

在弹出的样本量估计窗口将各参数值键入，如图2-8所示，在样本量n一行反复尝试填入不同数据，直至获得检验效能达到80%即为所求样本量，本例为每组303例。

图2－8 nQuery Advisor 7.0关于例2-4样本量估计的参数设置与计算结果

图2－9 SAS9.2关于例2-4样本量估计的参数设置与计算结果