单基地一阶海杂波的仿真研究
2012-05-18渤海船舶职业学院电气工程系
渤海船舶职业学院电气工程系 常 亮
1.引言
高频地波超视距雷达在探测海面过程中产生的海杂波的特性分析对雷达的整体性能起到了非常重要的作用,从1955年,Crombie开始提出一阶海杂波谐振散射的本质[1],从此对于海杂波的研究就被作为重要课题不断的被探索深入,在单基地高频地波超视距雷达中,由于Bragg谐振散射原理(当海浪波的波长等于雷达波长的一半时会发生Bragg谐振散射),在多普勒频域上可以看出两个幅度明显占优的峰线,也就是我们俗称的Bragg峰。方向为朝向雷达和远离雷达,是由一片海域内流动的海浪造成的,而在理想状态下,Bragg峰的多普勒频率值和雷达的波长即雷达的工作频率有关,所以在知道雷达频率的情况下我们可以精确的计算出Bragg峰的理论值。但是在实际情况中,海面会有洋流、风向的影响,而由海浪产生的一阶海杂波的Bragg峰也会偏离理想状态下的值。但是通过研究可以证实,这种多普勒频率上的偏移,不管是在朝向雷达方向还是在远离雷达方向上始终是保持一致的,经过多次测量发现其偏移量也大致相等,并且有一定的预知性。所以可以认为Bragg峰形态上的特征知识对目标检测与洋流测量也带来了极大的便利,为单基地海杂波检测提供了可靠的理论依据。本文简要叙述了单基地一阶海杂波的产生机理,并通过仿真进一步了解为后文的检测奠定了基础。
2.单基地高频雷达一阶海杂波理论
整体上来看,海面可以作为一个随机运动的散射体。但是实验证明,在理想条件下(不考虑洋流,风向,水深的影响),当高频雷达发射的电磁波波长的一半和海浪波波长相等时,会发生Bragg谐振散射原理,并且此时海浪波的方向为朝向雷达或者远离雷达。假设海浪波波长为sλ,雷达波长为λ,如果:

则发生Bragg谐振散射。如图1所示。
在无洋流的深水中,理论位置的一阶位置可以通过下式计算:

式中,λ为雷达的发射波的波长,fc为雷达的发射频率,g为重力加速度,c为光速。
海浪波的频率等同于谐振的多普勒频率,所以在回波功率谱上,在这两个频率点形成对称的尖锐谱峰,即我们所说的Bragg谐振散射原理,该点的多普勒频率就是一阶Bragg谐振频率。我们要研究的单基地一阶海杂波就是一阶Bragg谐振频率。
3.理想条件下的单基地一阶海杂波仿真
利用边界微扰法Barrick导出了在没有洋流、窄波束的情况下一阶海面散射系数表达式为:

公式中的参数,k为雷达的波矢,ωB=2πfB为Bragg角频率,φ为电磁波的方位角,ω为多普勒角频率,m=±1表示多普勒频移符号,S(·)为海浪的有向波高谱。
仿真结果如图2所示:理想状态下的一阶Bragg峰为两条对称的谱线,对数据按照Bragg频率归一化处理,可以发现一阶海杂波的Bragg峰发生在Bragg谐振散射位置。
现在根据仿真数据对单基地一阶海杂波的影响因素进行讨论:
3.1 雷达频率对单基地一阶海杂波的影响
结论:对比图3,随着雷达频率的升高,雷达的波长变短,对应产生谐振的海浪波长也相应的减小,所以对应的一阶海杂波散射系数增大。
3.2 海面风速对一阶海杂波的影响
结论:从图4我们可以明显的看出,随着海面风速的增加,海浪有向波高谱变大,对应的一阶海杂波的一阶散射系数变大。
3.3 风向的角度对一阶海杂波的影响
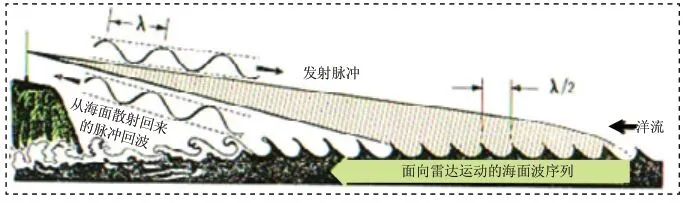
图1 高频地波超视距雷达一阶海杂波原理图

图2 理想状态下的一阶海杂波仿真

图3 不同雷达发射频率下的一阶海杂波仿真
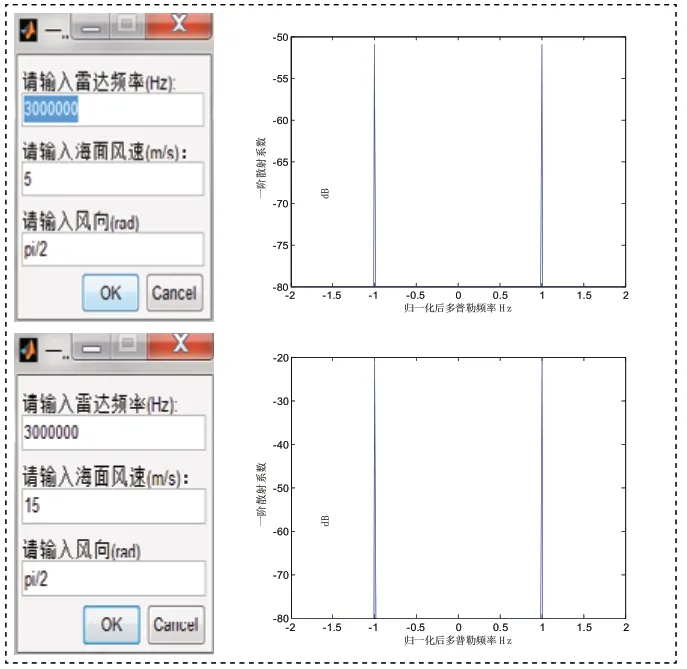
图4 海面风速不同的一阶海杂波仿真

图5 风向角度变化时的一阶海杂波仿真

结论:通过图5我们可以看出随着风向的改变对海杂波的正负bragg峰的影响也发生了改变,参考下图6单基地一阶海杂波实测数据,可以更清楚的观察到风向对一阶bragg峰的影响。
4.总结
在上文的仿真中我们可以看出,理想状态下Bragg峰表现为主瓣非常窄,幅值与雷达的发射频率和海面的风速密切相关。但是对实测数据进行分析可以发现主瓣周围常常会发现边带结构,尤其是当雷达的发射频率位于高频段靠近较高频区域,对其分析发现是由于电磁波和海浪波发生了二阶Bragg谐振散射造成的,从而形成了我们常说的二阶海杂波,经过大量的实际测量与观察二阶海杂波一般出现在一阶海杂波谱线之间和谱线两侧,并且可以证实二阶海杂波的峰值也是可以预测计算的,它们一般出现在以及2 fB处。通过上文的讲述,使得我们对一阶海杂波分析更加明确,通过仿真实验可以了解到,雷达频率,风向,风速等外在因素对一阶海杂波产生的影响,为第三章的实测数据处理奠定了基础。
[1]D.D.Crombie.Doppler Spectrum of Sea Echo at 13.67MHz.Nature.1955,175:681-682.
