浅水湖泊平面二维水质模型研究

朱文谨，周 凯

（淮海工学院土木工程学院，连云港 222006）

浅水湖泊平面二维水质模型研究

朱文谨，周 凯

（淮海工学院土木工程学院，连云港 222006）

磷氮元素在水体中迁移对湖泊富营养化研究具有重要性。采用有限元伽辽金加权余量法建立了简单的二维水质模型，并计算了在风场作用下的苏州市澄湖丰水期和枯水期的氮磷的分布以及输移。计算中引入了可由实测资料率定的可为正负的综合衰减参数，综合考虑了氮磷元素的沉降速率和释放速率，这样减少了水质多参数难确定的困难。计算的结果表明，流态与实际情况吻合较好，氮磷元素的浓度计算值与实测值相差不大。

磷氮元素；水质模型；综合衰减系数；澄湖

Biography：ZHU Wen-jin（1981-），male，doctor.

近年来，随着城市经济的发展，城市湖泊水体富营养化不断加剧，严重破坏了湖泊的生态环境。为了保护水库湖泊的水质，科学地利用水资源、必须对水库湖泊的富营养化状况进行有效的监测和预测。磷氮元素在水体中迁移规律对湖泊富营养化研究具有重要意义。现拟建一简单二维水质模型并计算澄湖（苏州市）中氮磷元素在水体中的迁移规律，通过对于模型的验证，证实建立模式的准确性，以期今后的研究中为浅水湖泊的富营养化预测和防治提供一定的参考［1-3］。

1 平面二维水流、水质模型

考虑到湖泊一般水深较浅，垂向流速变化较小，平面二维浅水湖泊水动力控制方程为［4-7］

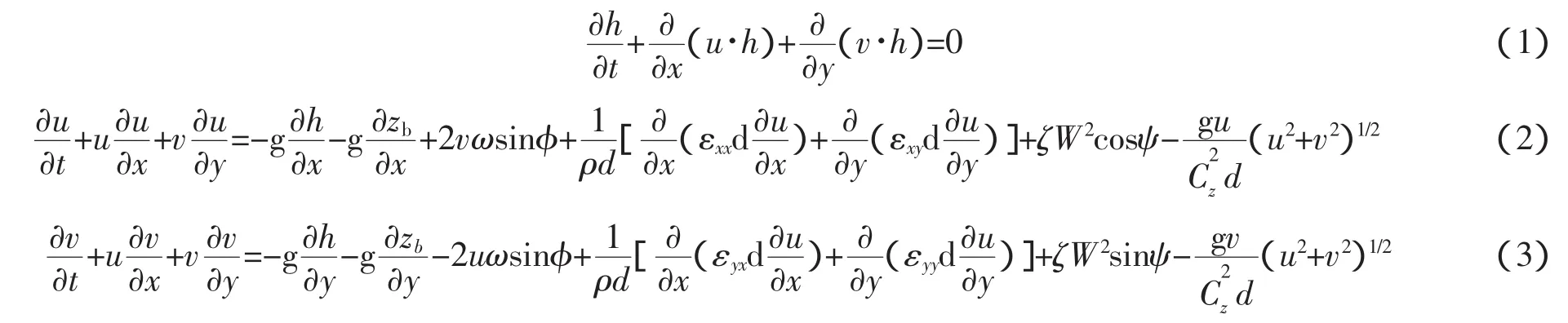
式中：u，v分别为x和y方向上的速度；h为水深；g为重力加速度；zb为河床高程；ρ为水密度；ζ为风应力的经验系数；W为风速；ψ为x正方向与风向之间的夹角；εij为涡粘性系数；C为谢才系数；ω为地球自转角速度；φ为当地纬度。

平面二维水质基本方程为

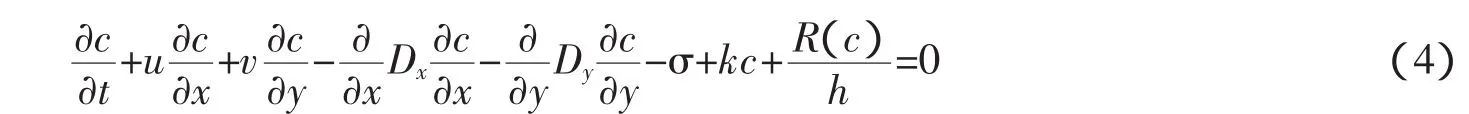
根据伽辽金（Galerkin）有限元法则描述控制方程（1）～（3）可写为

利用面积坐标的等参单元函数进行坐标变换，单元矩阵微分形式可表示为下面的形式（以水质方程为例）

式中：［k］为单元系数矩阵；［t］为时间矩阵；｛c｝为未知结点浓度向量；｛f｝为单元源、汇矢量。整体矩阵微分方程

采用Crank-Nicholson差分格式对该方程进行时间离散

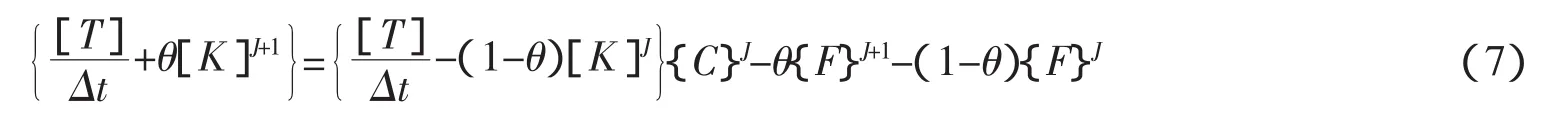
式中：θ为隐式差分系数；Δt为时间步长；J，J+1分别表示时刻。

2 模型的应用

澄湖地处苏州市东郊，西临太湖，北穿吴淞江与阳澄湖息息相通。位于东经120°41′，北纬31°22′，沿湖周长20 km，跨吴中区、昆山、吴江三地，全湖呈三角形，东西长度为9 km，南北长度为10.4 km，全湖面积56.06 km2，约5万亩，平均水深1.83 m，容积为0.73×108m3。澄湖河道大多数由西和西北方向注入湖泊，经东和东南方向排出泄入淀山湖辗转入黄浦江。湖泊水位主要受本地的降雨和吴淞江水位的双重影响。澄湖水位缓涨缓落，年内变幅较小，年中10月至次年2月为枯水期，水深1.70 m左右，3～5月先后入梅，水位上涨，水深1.80 m左右，6～9月为汛期，水位陡涨，水深2.50 m左右。

2.1 澄湖氮磷浓度的测定

以2005年12月下旬（枯水期）和2006年6月上旬（丰水期）所测的澄湖氮磷浓度为计算初始值，计算了枯季5个月，洪季4个月的氮磷浓度分布情况。在湖中心处布置一个采样点，河流入湖口周边布置了25个测点，每天采样2次的浓度平均后作为当天的浓度。同时测定相应水体的水温、pH值、溶解氧、总磷、总氮、亚硝酸氮、硝酸氮、氨氮、总有机碳、CODMn、叶绿素。

2.2 参数的选取及初边值条件

根据以往的研究成果、2次监测资料选取参数如下［8-9］：

（1）水动力力参数：曼宁糙率n值为0.015～0.019，涡粘性系数E取10～15 m2/s，纬度31.3°。

（2）水质参数：纵、横向扩散系数为1.0 m2/s，氮磷综合衰减系数（可为正负，综合考虑沉降速率释放速率。悬沙浓度为0.055 g/m3，中值粒径0.006 3 mm）采用实测资料估算和率定为：磷丰水期取8×10-4d-1，枯水期4×10-4d-1；氮丰水期取 4.7×10-3d-1，枯水期 3.6×10-3d-1。

计算中的初边值条件设定如下：

（1）初始条件：假定初始湖水是静止的，湖面是水平的，即：u（x，y）=v（x，y）=0。

（3）考虑了风对湖流的影响。根据实测资料，12月份为5～7级的北风，6月份为2～3级东南风。

2.3 数值计算及模型验证

进出澄湖的河道较多，而有些河道的流量很小甚至是没有流量，模型考虑主要几个影响较大的进出口。本文采用的有限元方法结合三角形网格，可以较好地贴合自然边界，提高了计算精度和计算效率。模型的网格在进出口处和部分较窄地方加密；由于湖中心附近水域的水深变化不大，流速较小，因此湖中心附近的网格较大，面积变化范围为32.53～40 529.84 m2。模型共布置三角形网格单元6 964个，结点数14 465个，网格划分如图1所示，计算区域见图2。

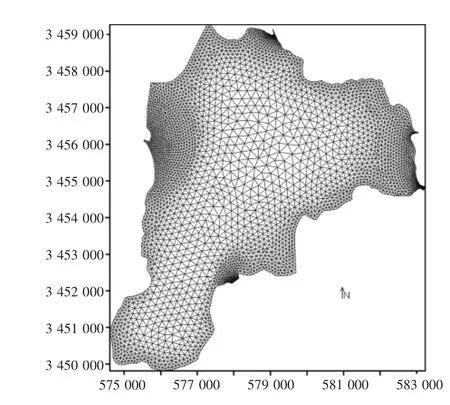
图1 计算水域网格图Fig.1 Mesh of computational domain

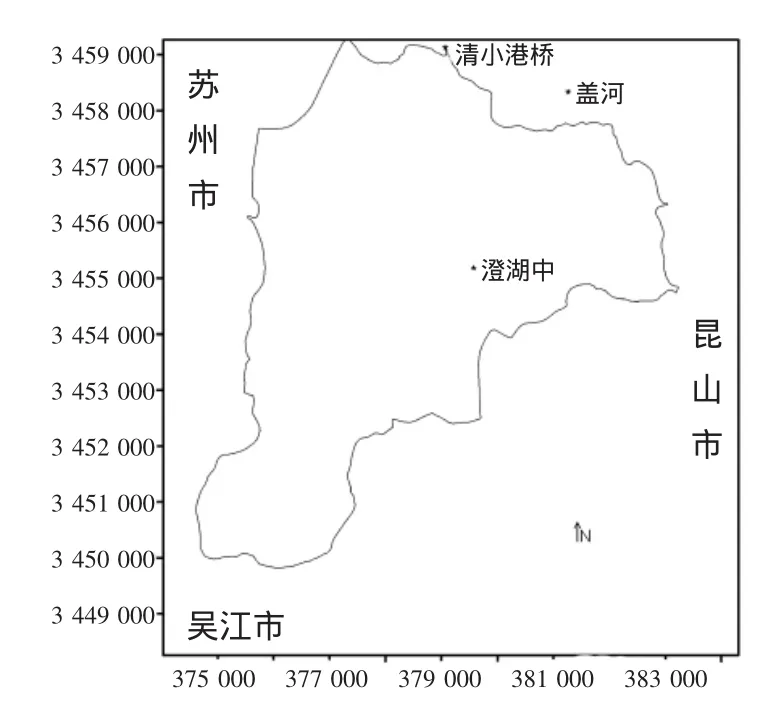
图2 计算区域示意图Fig.2 Sketch of Chenghu Lake

图3 澄湖12月份流场图Fig.3 Flow field of Chenghu Lake in dry season

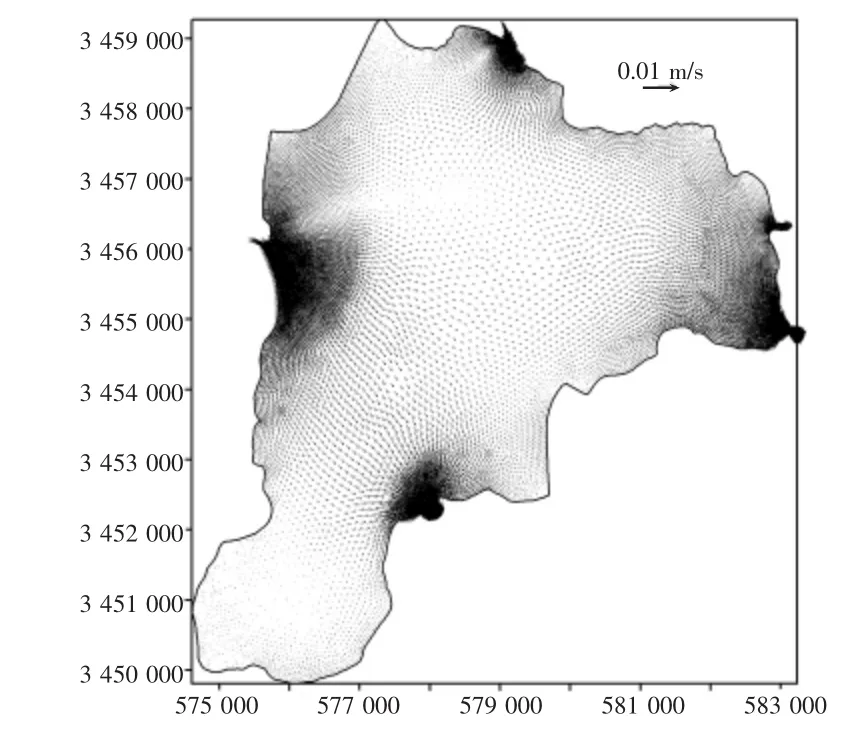
图4 澄湖6月份流场图Fig.4 Flow field of Chenghu Lake in flood season

为了能够清楚的显示出湖流，流场中大于0.01 m/s的速度均调整为0.01 m/s。由图3、图4可以看出，洪、枯季澄湖河道大多数由西和西北方向注入湖泊，经东和东南方向排出，各个进出口区域流场表现为吞吐流流态，而其余广大湖区流场表现为风生流，基本反映了澄湖的水动力特性。入湖流量小，湖中心位置的由于冬季的风速较夏季的大，湖中心的流速也较大一些。枯水期，总磷平均浓度0.533 mg/L、总氮平均浓度7.7 mg/L；丰水期，总磷平均浓度0.265 mg/L、总氮平均浓度6.26 mg/L（图5～图8）。

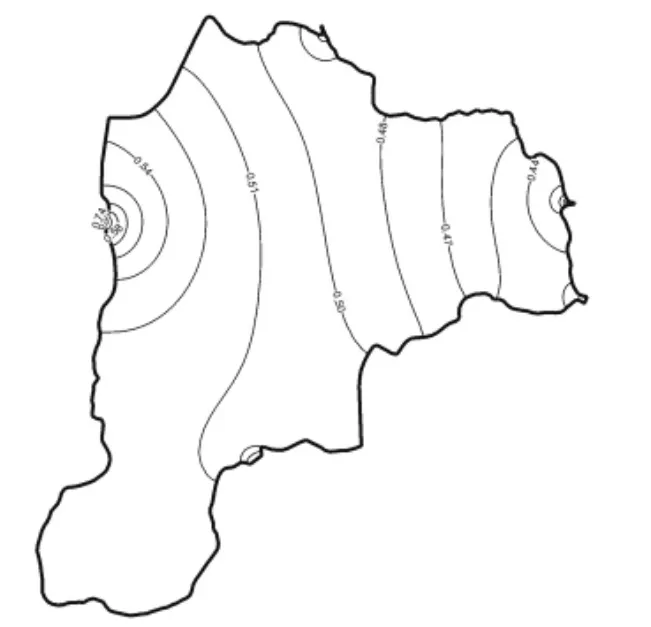
图5 澄湖丰水期总磷（TP）分布图Fig.5 Concentration distribution of TP in flood season

图6 澄湖枯水期总磷（TP）分布图Fig.6 Concentration distribution of TP in dry season

图7 澄湖丰水期总氮（TN）分布图Fig.7 Concentration distribution of TN in flood season

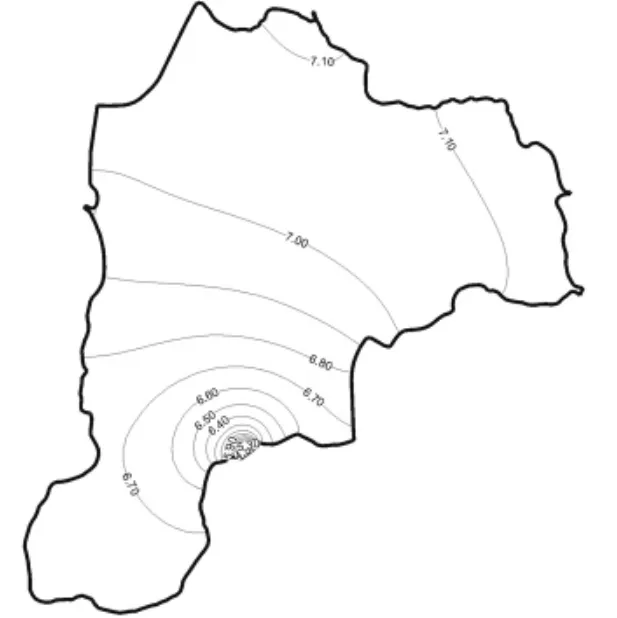
图8 澄湖枯水期总氮（TN）分布图Fig.8 Concentration distribution of TN in dry season

从模型计算的结果与实测值对比（表1～表3）可知，水动力模式计算的湖泊流速在清水港与大姚桥附近的精度较高，湖泊中心处水流流速的精度相对较低，这可能与湖泊中心处流速较小有关。水质模式计算的澄湖总磷和总氮的浓度值与实测值相差较小，基本能够反映洪枯季澄湖水质的总体情况。枯季澄湖地区的风速较大，从而湖泊中心的流速和风浪也较大，这可能造成湖泊底泥污染物的再悬浮和释放。而本文的水质模型采用单一综合衰减系数虽然可以考虑众多因素，但仍然不能够充分反映底泥释放的影响，所以造成了枯季湖泊中心处总磷浓度的计算值误差稍微偏大，达到18.181%（表3）。

表1 模型计算结果与实测结果验证流速表Tab.1 Verification of computation value and observation data for velocity m/s

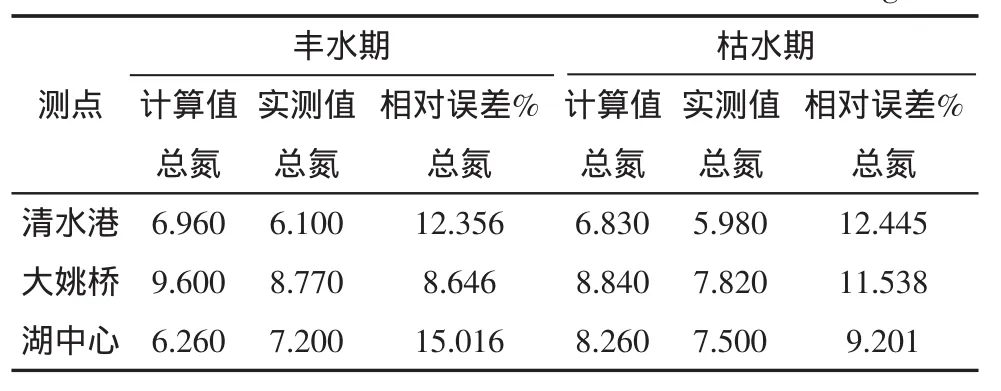
表2 模型计算结果与实测结果验证总氮表Tab.2 Verification of computation value and observation data for TN concentrationmg/L

表3 模型计算结果与实测结果验证总磷表Tab.3 Verification of computation value and observation data for TP concentration mg/L

3 结论

本文采用有限元伽辽金加权余量法对二维水流水质控制方程进行求解。模型对风场作用下的苏州市澄湖丰水期和枯水期的氮磷的分布以及输移进行了计算模拟。计算中引入了可由实测资料率定的一个综合衰减参数（可为正负），它综合考虑了氮磷元素的沉降速率和释放速率，这样减少了水质多参数难确定的困难。结果表明，数值计算值与实测值吻合较好，从而为澄湖的富营养化研究提供了实际可行的计算模型。但泥沙对污染物的吸附与释放是个动态过程，而模式中的综合衰减参数如何反应这一动态过程，尚需作更多的研究和实际验证。

［1］梅新敏，阮晓红，张兰芳，等.调引太湖水改善苏州市水动力条件研究［J］.环境科学与管理，2006，36（1）：60-62.

MEI X M，RUAN X H，ZHANG L F，et al.Research of Water Diversion From Taihu Lake to Improve the Water Environmental in Suzhou［J］.Environmental Science and Management，2006，36（1）：60-62.

［2］赵艳艳.金山湖二维水流水质数学模型研究［D］.南京：河海大学，2005：23-28.

［3］张锡辉.水环境修复工程学原理与应用［M］.北京：化学工业出版社，2002：13-15.

［4］李瑞杰，严以新，宋志尧.太平水道悬移质输运数学模型［J］.泥沙研究，2003（4）：5-7.

LI R J，YAN Y X，SONG Z Y．Calculation of Suspended Sediment Transport in Taiping Waterway［J］．Journal of Sediment Research，2003（4）：5-7．

［5］汪德爟.计算水力学理论与应用［M］.南京：河海大学出版社，1989：11-20.

［6］方子云.水资源保护工作手册［M］.南京：河海大学出版社，1988：43-57.

［7］櫆文信.河流海岸环境学［M］.武汉：武汉大学出版社，2004：78-92.

［8］高永霞，蔡琳琳，赵林林，等.丰水期环太湖河流与湖区水质比较研究［J］.环境科学，2011，32（10）：2 840-2 848.

GAO Y X，CAI L L，ZHAO L L，et al．Water Quality Comparison Between Lake Taihu and Contribute River During High Waterlevel Period［J］.Environmental Science，2011，32（10）：2 840-2 848．

［9］李晓静，娄安刚，王璟，等.青岛碱厂温排水对娄山河口附近水环境的影响预测［J］.水道港口，2011，32（2）：128-134.

LI X J，LOU A G，WANG J，et al．Prediction of environment effect near Loushan Estuary of thermal discharge by Qingdao Alkali Corporation［J］.Journal of Waterway and Harbor，2011，32（2）：128-134.

Two-dimensional model of water quality and its application in shallow lake

ZHU Wen-jin，ZHOU Kai
（School of Civil Engineering，Huaihai Institute of Technology，Lianyungang222006，China）

In order to predict the lake eutrophication，it is necessary to study the nutrients distribution such as phosphorus and nitrogen pollution.In this paper,the weighted residual method of finite element was used to establish the two dimensional depth-averaged water quality model.Then，the hydrodynamical movement and transport of nutrient material in Chenghu Lake were simulated with important functions.A comprehensive decay parameter of pollutant confirmed by field data was introduced in the calculation，which synthetically considered the settlement velocity and release speed of nitrogen and phosphorus at the same time.The results are in fair agreement with numerical data and observed data.

phosphorus and nitrogen；water quality model；comprehensive decay parameter；Chenghu Lake

X 824；O 242.1

A

1005-8443（2012）04-0353-05

2011-11-28；

2011-12-22

朱文谨（1981-），男，江苏省江都市人，博士，主要从事港口航道专业。