海底子母管线在规则波作用下的数值研究

成小飞，王永学，王国玉，任 冰

（大连理工大学海岸和近海工程国家重点实验室，大连 116024）

海底子母管线在规则波作用下的数值研究

成小飞，王永学，王国玉，任 冰

（大连理工大学海岸和近海工程国家重点实验室，大连 116024）

采用三步有限元法离散N-S方程，建立了数值波浪水槽模型。数值研究了规则波作用下海底子母管结构的水动力特性。对海底子母管线所受波浪力的数值结果与物模实验结果进行比较。基于该数值模型，还考察了不同的子母管间相对缝隙G/D（0.1，0.25，0.5，0.75）对海底子母管线水动力特性的影响。分析得到了不同G/D下海底子母管线的涡脱落特性以及管线水动力系数随G/D的变化规律。结果表明，数值结果和实验结果吻合较好，该数值波浪水槽模型可用来计算波浪作用在海底子母管线上的水动力。关于不同G/D，得到了2种不同的涡脱落模式，在G/D较小（0.1，0.25）时，为“反相同步脱落”模式，在G/D较大（0.5，0.75）时，为“同相同步脱落”模式。

海底子母管线；规则波；三步有限元；CLEAR-VOF；涡脱落

Biography：CHENG Xiao-fei（1985-），male，doctor student.

在实际工程中，不等直径的海洋输油气管线有时因为技术和经济的原因，经常以一定间隙捆在一起形成管束，置于海底。管束一般由一根母（大）管和几根子（小）管组成。一种比较流行的管束形式是海底子母管结构［1］，它由一根母管和一根子管组成，子管以一定间隙置于母管正上方。海底子母管结构与单管相比，其周围的流场形态及水动力特征更加复杂，所以关注这种海底子母管结构的水动力特性至关重要。

关于海底子母管线这种特殊结构，国内外很多学者已做了一些研究，主要集中在稳定流中，比如Kalghatgi等［2］采用拖车实验的方法研究得到了稳定流情况下，管线与海床的相对间隙、Re（Reynolds）数的变化对海底子母管线水动力系数的影响；Kamarudin等［3］、Zhao等［4］数值研究了稳定流情况下海底子母管线水动力问题，研究得到了不同Re数下子母管周围的压力分布，水动力系数以及涡脱落形式。

目前关于海底子母管线在波浪作用下的研究成果主要来自物模实验，比如马良等［5］和李玉成等［6］在波流水槽内研究了波流共同作用下KC（Keulegan-Carpenter）数对海底子母管线水动力系数的影响；Brankovic等［7］通过拖车造波的方式研究了波流共存下海底子母管线的水动力；Cheng等［8］在波浪水槽内着重研究了规则波和不规则波作用下海床对子母管线水动力的近壁影响。而目前仍缺乏关于海底子母管线在波浪作用下的数值研究。

本文采用三步有限元方法来离散二维粘性不可压流体的雷诺平均N-S方程和连续性方程，用k-ω模型来模拟流体的湍流运动，采用CLEAR-VOF方法来追踪运动水体的自由表面，构建了二维数值波浪水槽模型［9-10］。用该数值波浪水槽进行了海底子母管线在规则波浪场中受力的数值实验，并同物模试验结果进行比较验证，着重考察了子、母管间相对缝隙G/D（0.1，0.25，0.5，0.75）对海底子母管线水动力特性的影响。

1 基本控制方程

基本控制方程是二维粘性不可压雷诺平均N-S方程和连续性方程。在笛卡尔坐标系中无量纲化后的基本方程如下

式中：xi（i=1，2）为水平或垂直方向坐标；ui为i方向的速度分量；p为压力；k为湍动能；Re（=U0D/ν）为雷诺数，由母管中心位置处水质点的最大水平向速度U0、母管直径D和流体运动粘性系数v计算得到；t为无量纲化时间；νt为涡粘性；Sij为平均流动变形率张量，其方程如下

k-ω湍流模型［11-12］用来计算湍动能k和涡粘性νt，其方程如下

式中：ω=ε/（β*k）为湍动能比耗散率，ε为湍动能耗散率；pk=2νtSij∂ui/∂xj为湍动能生成项；涡粘性νt由下式计算得到

式（4）～式（6）中各模型参数定义如下

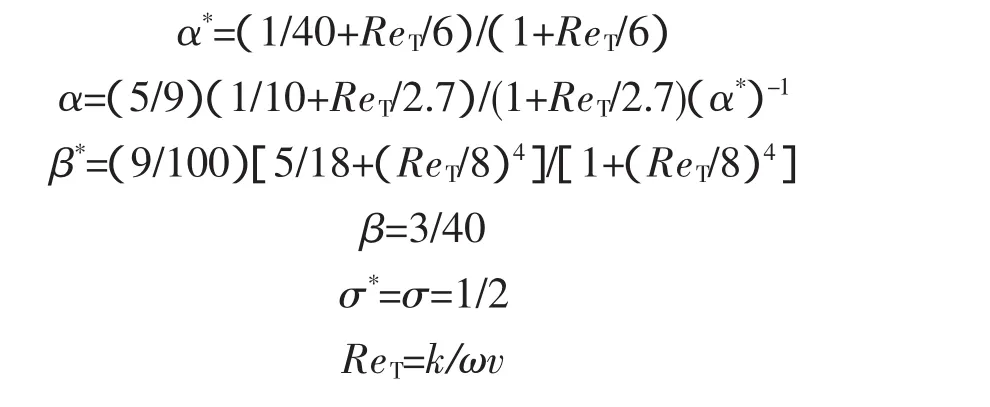
2 数值计算方法

本文对基本控制方程的求解采用三步有限元法［13］，即将时间导数按泰勒级数展开，一个时间步内分3次进行迭代，以获得稳定的数值解。与SUPG等传统迎风有限元方法相比，三步有限元法数值解精度高（三阶），数值实现过程简单，并具有更高的计算效率。N-S方程（1）应用三步有限元法，可得到如下时间离散形式

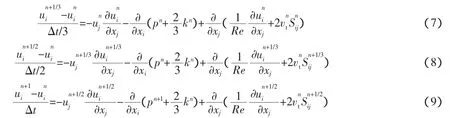
式中：上标 n，n+1/3，n+1/2 和 n+1 分别表示 n，n+Δt/3，n+Δt/2 和 n+Δt时刻的量值。式（7）～式（9）可用标准的Galerkin加权余量有限元法进行空间导数离散。

针对本文的湍流动问题，式（7）～式（9）中k和vt不是常数，需要进行线性化处理，即利用上一时刻的流场计算结果，根据k-ω湍流模型式（4）～式（6）求得k和vt，并在当前时间步内将之视为常数添加到式（7）～式（9）中。其中对于k-ω湍流模型，其控制方程也是对流扩散方程类型，形态上同于N-S方程，因此对式（4）～式（6）的离散和求解也可参照N-S方程的处理方法。

本文建立数值波浪水槽，可反映出计算域中自由表面的实时变化特征。在任意时间步内，通过三步有限元法数值求解N-S方程，得到该时间步对应的速度场和压力场后，对计算域内的自由表面进行重构。关于自由表面的重构本文采用的是Ashgriz等［14］提出的CLEAR-VOF（Computational Lagrangian-Eulerian Advection Remap Volume of Fluid）方法。它是以有限元为基础的一种高效的自由表面重构技术。CLEAR-VOF方法是在欧拉网格基础上采用了拉格朗日思想追踪单元内水团在新时刻的位置以求解每个单元内VOF函数。那么在经历一个时间步Δt后，水团顶点的位移和新位置可表示为

水团几何顶点新位置确定后，水团位置也由此得到。这种方法的主要优点包括无需求解关于流体体积函数的微分方程，而是在拉格朗日意义下实现流体的对流输运；界面重构对具体的网格划分方式无特殊要求，不但适用于规则网格，同时也可用于非规则网格。

3 数值波浪水槽

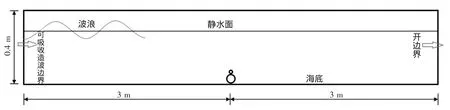
图1 数值波浪水槽计算域Fig.1 Computational domain of numerical wave flume

数值波浪水槽计算域如图1所示，水槽长6 m，高0.4 m，水深0.3 m。海底子母管结构如图2所示，位于水槽中央，母管直径D为0.02 m，子管直径d为0.008 m，母管与海底之间的间隙比e/D=0.25，子母管之间的相对缝隙G/D=0.25，海底及管线表面均光滑，不考虑粗糙率的影响。

对计算域采用四边形线性等参元进行网格划分。图3给出了子母管结构周围的网格划分详细图。整个计算域网格共有61 530个节点，60 784个单元，网格的最小尺寸约为0.000 5 m，最大尺寸约为0.03 m，时间步长为0.001 s。

计算域左边界和右边界分别设为可吸收式无反射造波边界与开边界［15］，海底和管线表面为无滑移边界条件，水平和垂向速度均为零，计算域顶表面为滑移边界条件，垂向速度为零。初始时刻，流体是静止的，整个计算域的速度和压力都设为零。

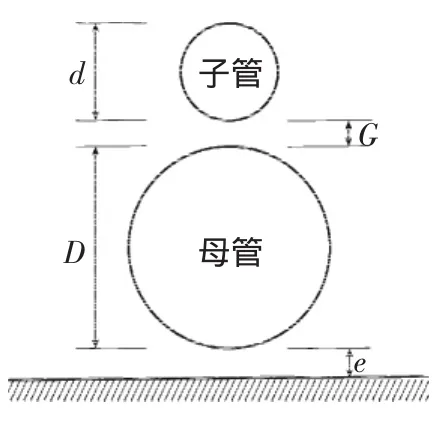
图2 海底子母管结构Fig.2 Submarine piggyback pipeline configuration

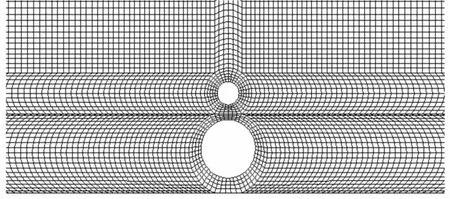
图3 子母管周围的网格（e/D=G/D=0.25）Fig.3 Meshes near the piggyback pipeline（e/D=G/D=0.25）

4 数值计算结果和实验结果的比较

为了验证数值波浪水槽模型的可靠性，本文将数值计算的结果和物模实验结果进行比较。物模实验在大连理工大学海岸与近海工程国家重点实验室海洋环境水槽中进行，通过水下双向测力传感器同步测得了海底子母管系统在规则波作用下总的水平力和升力（垂向力）。关于物模实验的细节另文给出。为了便于比较，物模实验工况和数值计算的工况选为一致。

图 4给出了波高 H=0.1 m，周期 T=1.7 s，水深 h=0.3 m，e/D=G/D=0.25条件下（KC=25.14，Re=5 880），由数值波浪水槽计算得到的波面历时过程线（波面过程线的采样点在管线中心位置正上方）、子母管系统所受总的水平力和升力历时过程线与实测结果的比较。由图4可知，数值计算得到的波面过程线、水平力过程线与实测数据结果吻合较好，两者在幅值上基本相同，相位也基本吻合。两者升力过程线在幅值和相位上也大体一致，但是在一个波周期内，实测升力过程线比数值计算升力过程线多一个或几个小的峰（谷）值，这是由于实验条件下升力的随机性很大，波浪场中微小的扰动即可造成升力的变化。从整段升力过程线来看，数值计算与实测结果基本吻合。综上分析，本文采用的数值计算方法是可靠的，建立的数值波浪水槽模型可以用来计算波浪作用下海底子母管线的受力。

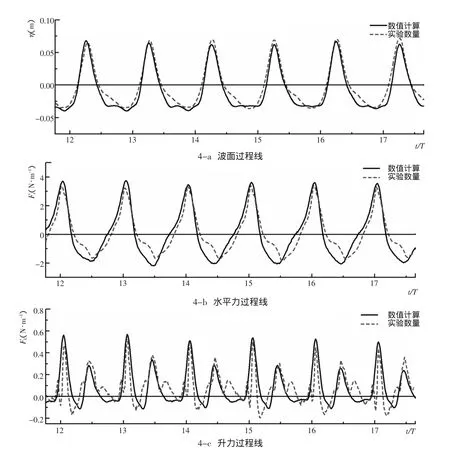
图4 数值计算结果与物模实验结果的比较（KC=25.14，e/D=G/D=0.25）Fig.4 Comparison of numerical and experimental results（KC=25.14，e/D=G/D=0.25）

5 G/D对海底子母管线水动力特性的影响

基于本文建立的数值波浪水槽模型，考察了子母管间的相对缝隙G/D（0.1，0.25，0.5，0.75）对海底子母管线水动力特性的影响，分析得到了在不同G/D下海底子母管线的涡脱落特性以及管线水动力系数随G/D的变化规律。在数值计算中，取子管与母管管径之比d/D为0.4，母管与海床间隙比e/D为0.25，波浪为规则波（波高 H=0.1 m，周期 T=1.7 s），相应 KC=25.14。

5.1 涡脱落特性

图5分别给出了不同G/D（0.1，0.25，0.5，0.75）下，海底子母管线（子管、母管、子母管系统）在一个波浪振荡周期内（t/T=7.4～8.4）所受水平力Fx和升力FL的历时过程线。从图5可以看出，子管、母管和子母管系统所受水平力Fx在4种G/D下均同步振荡，与波浪振荡频率相同，但是所受升力FL比较复杂，其振荡频率是两倍甚至三倍的波浪振荡频率。在G/D较小时（G/D=0.1），子管和母管所受升力相互排斥，反相振荡，这是因为G/D较小时子、母管之间的相互干扰较明显。随着G/D的增大，子、母管间的相互干扰逐渐减弱，子管和母管升力的振荡趋于同步。子母管系统所受波浪力的历时过程线与母管的非常接近，这主要跟母管管径相对较大，在子母管系统中占主导地位有关。

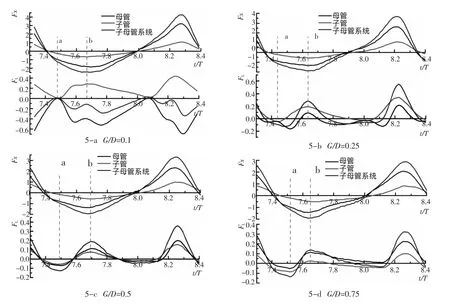
图5 不同G/D下海底子母管线水平力和升力的历时过程线Fig.5 Time histories of in-line and lift forces on submarine piggyback pipeline for different G/D

在图5中不同G/D（0.1，0.25，0.5，0.75）对应的波浪力历时曲线，取其前半周期升力曲线出现的2个极值时刻 a、b，考察其管线周围涡量的分布特性。图 6 分别给出了不同 G/D（0.1，0.25，0.5，0.75）下，在瞬时 a、b（对应于图 5 中的瞬时 a、b）海底子母管线周围涡量的分布图。涡量 wz由公式 wz=0.5×（∂u2/∂x1-∂u1/∂x2）计算得到，图6中的虚线表示涡量值为负（负涡），实线表示涡量值为正（正涡）。由图6-a、6-b的涡量分布图可见，子母管间缝隙较小，子管与母管缝隙间的涡因受到抑制较小，而子管顶部和母管底部的涡不断增大，在时刻a，子管顶部的负涡和母管底部的正涡同时在管线右侧脱落，引起子、母管升力达到极值，而且两者受力是反相的（如图5-a、图5-b），称为“反相同步脱落”模式。随着波浪水质点速度的转向，母管右侧的正涡先转向反作用在母管上，引起母管升力达到极值。随后在时刻b，子管右侧脱落的负涡也发生转向，同时作用在子管和母管上，引起子、母管所受水平力和升力均达到极值。

图6 不同G/D下海底子母管线周围涡量的分布图Fig.6 Vorticity contours around submarine piggyback pipeline for different G/D

由图6-c、图6-d的涡量分布图可见，在G/D较大时（0.5，0.75），子管与母管缝隙间的涡所受抑制逐渐减弱，子母管间缝隙处的涡逐渐增大。在时刻a，子管顶部的负涡和母管顶部的负涡均在管线右侧同步脱落，引起子、母管所受升力达到极值，并且由图5-c、图5-d可以看出，子、母管所受升力同相，称为“同相同步脱落”模式。随后在时刻b，由于波浪水质点速度的转向，子管右侧脱落的负涡和母管右侧脱落的负涡均发生转向，分别反作用在各自的管线上，引起各自管线所受升力达到极值。

由以上分析，可以得到波浪作用下，管线周围涡的脱落或者脱落涡的反作用都会引起管线所受水平力或者升力达到极值。在G/D=0.1，0.25时，子管对母管的影响较大，母管不仅受到母管自身脱落涡的反作用产生升力极值，同时还受到子管脱落涡的反作用产生极值。而随着G/D的增大，子管对母管的影响逐渐减小，在G/D=0.5，0.75时，母管仅受到自身脱落涡的反作用。因此从涡的脱落特性，可以说明图5中在G/D=0.1，0.25时，母管所受升力的峰（谷）值个数要多于G/D=0.5，0.75时的情形。

图 7 分别显示了不同 G/D（0.1，0.25，0.5，0.75）对应的子管、母管和子母管系统的无量纲Strouhal数。St=f0D0/U0，其中f0为管线升力的振荡频率；D0为管线直径，子、母管和子母系统分别取d，D和等效直径DE（DE=D+d+G）；U0为来流速度，本文取母管中心位置处波浪的水质点水平速度。从图7可以看出，在G/D=0.1，0.25时，子管仅存在单一St数，而母管和子母管系统存在2个St数，这是因为在G/D较小时，子管对母管的影响较大，子管脱落的涡对母管也有额外的反作用。随着G/D的增大，子管脱落的涡对母管的反作用减弱，在G/D=0.5，0.75时，子管、母管和子母管系统均只存在单一St数。另外，由图7中各管线St数的比值关系还可以发现，子、母管和子母管系统升力振荡的主频率是相同的，均是波浪振荡频率的2倍，而在G/D较小时还存在3倍于波浪振荡频率的次频。

图7 不同G/D下海底子母管线的St数Fig.7 Stnumbers of submarine piggyback pipeline for different G/D

5.2 水动力系数

在波浪作用下，管线所受水平力和升力可按Morison方程计算得到

式中：Fx（t）为管线所受的水平波浪力；FLmax为管线所受的最大升力；ρ为流体密度；l为管线的长度；u（t）、a（t）分别为流场未受扰动时母管中心位置处波浪的水质点水平速度和加速度；umax为流场未受扰动时母管中心位置处波浪的最大水质点水平速度；D0为管线直径，子、母管和子母系统分别取d，D和等效直径D（EDE=D+d+G）；CD、CM和CL分别为管线的拖曳力系数、惯性力系数和升力系数。

CD和CM可由最小二乘法计算得到，而升力系数C（L，升力方向背离海床；，升力方向指向海床）由极值法计算得到。关于水动力系数的详细分析方法可参考李玉成等［16］。图8分别给出了在规则波作用下（KC=25.14）海底子母管结构中子管、母管和子母管系统的水动力系数CD，CM，CL随间隙比G/D的变化规律。

从图8可以看出，子管、母管和子母管系统的CD，CM关于G/D的变化规律大体一致，均随G/D的增大而减小，并且母管和子母管系统的CD，CM值比较接近，这跟母管在子母管系统中占主导地位有关。子管的CD，CM值要小于母管和子母管系统的CD，CM值，是后者的65%～90%。子管和母管的升力系数CL关于G/D的变化规律是相反的，子管的随G/D的增大而减小，的绝对值随G/D的增大而增大，这是因为在G/D较小时，母管的存在抑制了子管底部涡的发展，导致子管很小较大，随着G/D的增大，母管的影响逐渐减弱绝对值不断增大，不断减小。相反，母管的随G/D的增大而增大的绝对值随G/D的增大而减小。另外，子母管系统的升力系数随G/D的变化趋势同母管大体一致，量值上也比较接近。

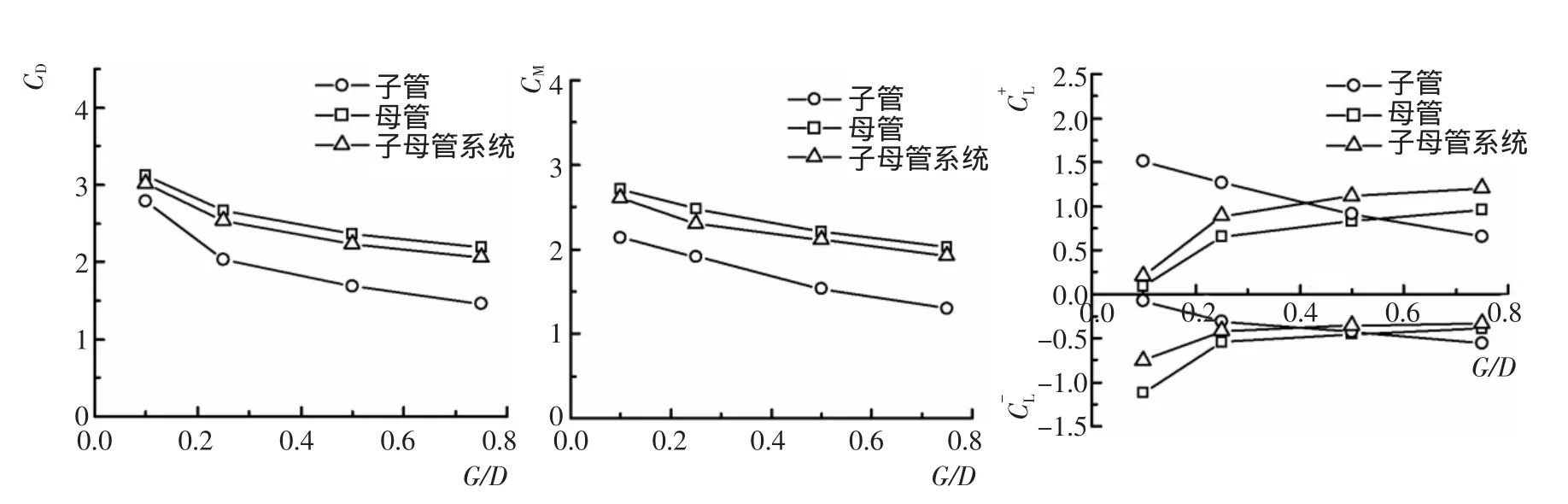
图8 海底子母管线水动力系数随G/D的变化规律Fig.8 Variation of hydrodynamic coefficients on submarine piggyback pipeline with G/D

6 结论

本文采用三步有限元法来离散N-S方程，k-ω模型来模拟流体的湍流运动，CLEAR-VOF方法来追踪运动水体的自由表面，建立了规则波作用在海底子母管线上的数值波浪水槽模型，将数值计算结果同物模实验结果进行了比较验证。并考察了在KC=25.14条件下，子母管间的相对缝隙G/D（0.1，0.25，0.5，0.75）对海底子母管线水动力特性的影响。其主要结论如下：

（1）经比较验证，本文所建立的数值波浪水槽模型可以用来计算海底子母管线在规则波作用下的水动力。

（2）关于不同G/D，本文得到了海底子母管线在规则波作用下2种不同的涡脱落模式。在G/D=0.1，0.25时，存在一种涡脱落模式称为“反相同步脱落”模式；在G/D=0.5，0.75时，存在另一种涡脱落模式称为“同相同步脱落”模式。

（3）子管、母管和子母管系统的C，C关于G/D的变化趋势大体一致，均随G/D的增大而减小。子管的DM随G/D的增大而减小，的绝对值随G/D的增大而增大，母管的升力系数随G/D的变化趋势与子母管系统相一致，但与子管的变化趋势相反。

［1］杨琥，倪浩，朱晓环.一种新型的置换海底子母管道技术［J］.中国造船，2007（48）：563-570.

YANG H，NI H，ZHU X H.An applicable replacement bundled pipeline structure for offshore marginal oilfield development［J］.Shipbuilding of China，2007（48）：563-570.

［2］Kalghatgi S G，Sayer P G.Hydrodynamic forces on piggyback pipeline configurations［J］.Journal of Waterway，Port，Coastal，and Ocean Engineering，1997，123（1）：16-22.

［3］Kamarudin M H，Thiagarajan K P，Czajko A.Analysis of current-induced forces on offshore pipeline bundles［C］//Witt P J.Proceeding of 5th International Conference on CFD in the Process Industries.Melbourne：CSRIO Australia，2006.

［4］ZHAO M，CHENG L，TENG B.Numerical modeling of flow and hydrodynamic forces around a piggyback pipeline near the seabed［J］.Journal of Waterway，Port，Coastal，and Ocean Engineering，2007，133（4）：286-295.

［5］马良，王金英，孙绍述，等.海底（子-母）管道在波浪作用下水动力载荷的实验研究［J］.大连大学学报，1993，3（4）：54-63.

MA L，WANG J Y，SUN S S，et al.Experimental study of hydrodynamic force loading under the action of wave current on submarine composite pipelines［J］.Journal of Dalian University，1993，3（4）：54-63.

［6］李玉成，张宁川，孙姎.波流共同作用下近底子母管线的水动力特征［J］.水动力学研究与进展，1994，9（1）：51-59.

LI Y C，ZHANG N C，SUN Y.The hydrodynamic characteristic of submarine composite pipeline in wave-current coexisting field［J］.Journal of Hydrodynamics，1994，9（1）：51-59.

［8］CHENG X F，WANG Y X，WANG G Y.The effect of the seabed proximity on the hydrodynamic forces of the piggyback pipeline under wave action［C］//Chung J S.Proceeding of 30th International Conference on Ocean，Offshore and Arctic Engineering.New York：ASME，2011.

［9］LU L，LI Y C，TENG B，et al.Numerical simulation of turbulent free surface flow over obstruction［J］.Journal of Hydrodynamics，2008，20（4）：414-423.

［10］孙英伟，陈兵，康海贵.远破波作用数值模拟的 CLEAR-VOF 模型［J］.水科学进展，2010，21（6）：795-800.

SUN Y W，CHEN B，KANG H G.Numerical simulation of broken wave with the CLEAR-VOF-FEM model［J］.Advances in Water Science，2010，21（6）：795-800.

［11］Wilcox D C.Reassessment of the scale-determining equation for advanced turbulence models［J］.AIAA Journal，1988，26（11）：

1 299-1 310.

［12］Wilcox D C.Simulation of transition with a two-equation turbulence model［J］.AIAA Journal，1994，32（2）：247-255.

［13］JIANG C B，Kawahara M.The analysis of unsteady incompressible flows by a three-step finite element method［J］.International Journal of Numerical Methods in Fluids，1993，6：793-811.

［14］Ashgriz N，Barbat T，WANG G.A computational Lagrangian-Eulerian advection remap for free surface flows［J］.International Journal of Numerical Methods in Fluids，2004，44：1-32.

［15］王永学.无反射造波数值波浪水槽［J］.水动力学研究与进展，1994，9（2）：205-213.

WANG Y X.Numerical wave channel with absorbing wave-maker［J］.Journal of Hydrodynamics，1994，9（2）：205-213.

［16］李玉成，陈兵，王革.波浪对海底管线作用的物理模型实验及数值模拟研究［J］.海洋通报，1996，15（4）：58-65.

LI Y C，CHEN B，WANG G.Physical model test and numerical simulation of pipeline under wave action［J］.Marine Science Bulletin，1996，15（4）：58-65.

Numerical study of submarine piggyback pipeline under regular wave action

CHENG Xiao-fei，WANG Yong-xue，WANG Guo-yu，REN Bing
（State Key Laboratory of Coastal and Offshore Engineering，Dalian University of Technology，Dalian116024，China）

A numerical wave flume model was established，in which the Navier-Stokes equation was dispersed using the three-step finite element method.Then the hydrodynamic characteristics of the submarine piggyback configuration under regular wave action were numerically studied.The numerical results for wave forces on submarine piggyback pipeline were compared with the experimental results.Based on this numerical model，the effect of the spacing ratios between the small and the large pipelineG/D（0.1，0.25，0.5，0.75）on the hydrodynamic characteristics of the submarine piggyback pipeline was also investigated.The vortex shedding characteristics of the piggyback pipeline about differentG/Dand the variation of hydrodynamic coefficients of the pipeline withG/Dwere presented in this paper.The results show that both numerical and experimental results are in good agreement,and the numerical wave flume model can be applied to predict the hydrodynamic forces on the submarine piggyback pipeline under wave action.Two different vortex shedding patterns are found about differentG/D.One is the“anti-phase-synchronized”pattern forG/D=0.1，0.25，the other is the“in-phase-synchronized”pattern forG/D=0.5,0.75.

submarine piggyback pipeline；regular wave；three-step finite element;CLEAR-VOF；vortex shedding

TV 139.2；O 242.1

A

1005-8443（2012）03-0185-09

2012-01-05；

2012-03-23

国家自然科学创新研究群体基金（50921001）；国家重点基础研究发展计划（973计划）（2011CB013702）

成小飞（1985-），男，江苏省南通人，博士研究生，主要从事波浪与海洋结构物的作用研究。