含有极大值的二阶差分方程的有界振动性和非振动性

刘雪飞， 钟晓珠， 许红叶， 王寅琮， 赵 芬

(燕山大学 理学院 河北 秦皇岛 066004)

0 引言

由于差分方程的广泛应用，对它的研究也随之越来越多，特别是对差分方程解的振动性的充要条件的研究有了较多的研究成果[1-3].文献[4-6]对含有极大值的一阶差分方程进行了研究，但是对含有极大值的二阶差分方程的研究却很少.作者研究了含有极大值的二阶差分方程

(1)

其中，[n-l,n]={n-l,n-l+1,…,n}，l,k为正整数，{qn},{rn}为非负实数列，{pn}为实数列.

方程(1)的解{xn}如果既不最终为正，也不最终为负，就称为振动的，否则，就称为非振动的.如果方程(1)的所有解都是振动的，方程(1)就称为振动的.

定义

zn=xn-pnxn-k，

(2)

则由(1)可得

(3)

1 引理

引理1(Ⅰ) 若pn≤-1且{xn}为(1)的正有界解，则{zn}非减且zn>0；

(Ⅱ) 若pn≤-1且{xn}为(1)的负有界解，则{zn}非增且zn<0.

证明(Ⅰ)因为{xn}为(1)的正有界解，由(3)可得

(4)

所以{Δzn}为非增的.

因为zn=xn-pnxn-k，且{xn}为(1)的正有界解，pn≤-1，所以zn>0且{zn}有界.下面证明当n≥n0时，Δzn≤0.

否则∃n1，使得n1≥n0，当n≥n1时有Δzn>0，由(4)可知Δzn≤Δzn1.从n1加到n-1，得zn-zn1≤(n-n1)Δzn1，当n→时，则zn→+与{zn}有界矛盾，所以Δzn≤0，则{Δzn}为非增的，(Ⅰ)得证.

(Ⅱ)因为(2)成立，且{xn}为(1)的负有界解，pn≤-1 ，所以zn<0且{zn}有界.下面证明Δzn≥0.

当n≥n0时，证明方法同(Ⅰ)，当n→时，则zn→-与{zn}有界矛盾，所以 Δzn≥0，则{Δzn}为非减的，(Ⅱ)得证.

引理2若

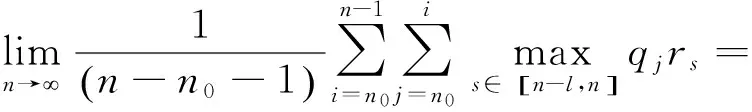
(H1)

成立，当0≤pn≤1，{xn}为(1)的正解时，则{zn}单增且zn>0.

根据(4)可知

(5)

将(5)式从n0加到i,得

(6)

将(6)式从n0加到n-2,得

由(H1)可知，当n→时，zn→-与{zn}有界矛盾，则zn>0.下面证{zn}单增.

当n≥n4时，Δzn>0.否则∃n5，使得n5≥n4，当n≥n5时，Δzn≤0，由(4)知，当n≥n5时,

Δzn≤Δzn5

，

(7)

将(7)式从n5加到n-1,得

zn-zn5≤(n-n5)Δzn5,

当n→时，有zn→-，与zn为正矛盾，则Δzn>0，{zn}单增得证.

2 定理

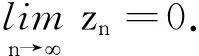
因为{xn}为(1)的正解, 且pn≤-1，则zn=xn-pnxn-k>0.由引理1知{zn}非增且zn>0.∃T=

例如：教师在给学生讲解地理相关的地形地貌的时候，可以为学生搜集相关的图像，让学生能够对我们国家复杂的地貌有一个具体的了解，这样学生就会在接下来的学习过程中更加的积极主动，能够把自己的注意力集中到学生地理知识上来，提高教师课堂的教学效果。

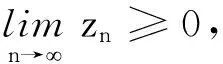
(8)

将(8)式从n0加到i，得

(9)

将(9)式从n0加到n-2，得

由(H1)可知，当n→时，zn→-与zn=xn-pnxn-k>0产生矛盾，得证.

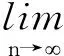
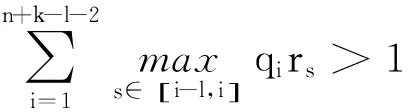
证明假设{xn}为方程(1)的最终正解，根据已知条件和引理2知，Δzn>0且zn>0.

由(2)知xn≥zn，同理可得出xs≥zs，则根据(3)得

(10)

将(10)式从n加到n+k-l-2，且zn>0，有

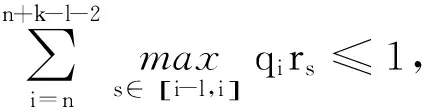
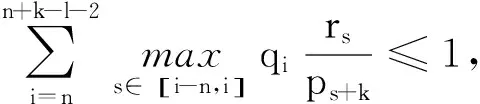
证明(ⅰ)首先证明zn<0.

假设zn≥0，设xn为方程(1)的一个最终正解，根据(2)且pn≥1，则xn≥pnxn-k≥xn-k，所以{xn}有下界，∃M>0,当n≥n0时，xn≥M.

由(3)知

(11)

将(11)式从n0加到i-1,得

(12)

将(12)式从n0加到n-1，得

因为(H1)成立，当n→时，有zn→-,与假设中zn≥0矛盾，则zn<0得证.

(ⅱ) 再证Δzn<0.

假设Δzn≥0，由(3)可知，Δzn是非增的，当n≥n1时，则Δzn1≥Δzn.从n1加到n得zn-zn1≤(n-n0+1)Δzn1，当n→时，则zn→+与(ⅰ)矛盾，(ⅱ)得证.

(ⅲ)由zn=xn-pnxn-k<0知,xn=zn+pnxn-k>0，则有zn>-pnxn-k.

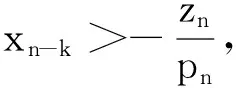
由(ⅱ)和(3)得

(13)

将(13)式从n加到n+k-l-2，得

由Δzn<0知

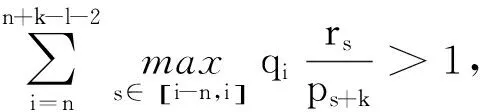
同理，当xn为方程(1)的一个最终负解时，可得出矛盾，所以方程(1)的所有解振动.

参考文献：

[1] 李玉梅，王幼斌，范叶华．一阶中立型差分方程的振动性[J].数学的实践与认识，2007，36(21):188-191.

[2] 韩振来，孙书荣，时宝.具有连续变量的多时滞二阶非线性中立差分方程的振动性[J]．生物数学学报，2007，22(2):293-297.

[3] 唐清干，曾玲．高阶中立型差分方程的振动性及其非振动解的渐近性态[J].数学杂志，2000，20(2)：207-210.

[4] 罗交晚，刘正荣，俞元洪.带有极大值项的中立型差分方程的振动性和非振动性[J].应用数学学报，2002，25(3)：385-391.

[5] 武冬.带有极大值项的一阶中立型差分方程解的振动性和非振动性[J].青岛海洋大学学报：自然科学版，2003，33(6)：975-982.

[6] 范彩霞，赵爱民，邓嵩.带有极大值项的中立型差分方程的振动性[J].山西大学学报：自然科学版，2005，28(1)：5-7.