中国股指收益率的非对称拉普拉斯分布实证检验

曾五一，刘 飞

（厦门大学 经济学院，福建 厦门 361005）

中国股指收益率的非对称拉普拉斯分布实证检验

曾五一，刘 飞

（厦门大学 经济学院，福建 厦门 361005）

应用非对称拉普拉斯分布拟合沪深两市股指日、周收益率数据。研究结果表明：非对称拉普拉斯分布能够比正态分布更好地反映两市股指的日、周收益率数据的尖峰、厚尾、偏态特征。由于非对称拉普拉斯分布有显性的表达式，便于开展参数估计和数字特征的计算，因此对于股指期货投资者而言，在计算股指收益率的VaR、CVaR进行风险测量时，采用非对称拉普拉斯分布将是较好的选择。

非对称拉普拉斯分布；股指收益率；尖峰；厚尾

一、研究背景

股指收益率的分布一直是金融研究中的一个重要问题。中国已从2010年4月16日起正式推出交易股指期货。研究中国股指收益率的分布，不仅有助于认识股票市场的内在运行规律，而且还可以帮助股指期货投资者正确进行风险度量，以便进行资产定价与资产组合选择。

20世纪50年代，Kendall和Osborne通过对英美股市收益率的数据分析，得出了股票资产的收益率近似服从正态分布的结论［1－2］。在过去几十年里，基于金融资产收益率正态分布假定发展起来的经典理论，如Black－Scholes Option Pricing Model（BSM）和 Value at Risk（VaR）等在学界和业界得到了广泛的应用。但是，近年来许多学者研究发现，现实中金融资产收益率分布常常明显偏离正态分布的假定，呈现尖峰、厚尾、偏态的特征，因此如何修正正态分布的假设，提出能够更好地拟合金融资产收益率的分布，成为金融研究的一项新的课题。

为此，许多学者进行了大量的研究。比如，Mandelbrot等提出了用稳定帕雷托分布（Stable Paretian）来拟合股市收益率分布尖峰、厚尾、偏态的特征［3－4］；徐龙炳等应用稳定分布对中国股票收益率进行分布拟合，研究结果显示中国股指收益率具有尖峰、厚尾、偏态的分布特征［5－6］。尽管学者们通过用稳定分布来拟合金融资产收益率的分布，取得了一定进展，但是由于稳定分布是用特征函数来表示的，概率密度函数没有显性的解析表达式，且含有4个参数，又缺乏合理的经济解释，这就给进一步研究带来了困难。而且，根据稳定分布，当a∈［1，2］时，方差变成无定义或无极限，在这种情况下，样本方差作为风险度量指标就会失去意义。

针对上述问题，Kozubowski T．等提出用由指数分布和正态分布构成的非对称拉普拉斯分布刻画股票收益率，运用该分布不仅能够拟合收益率数据的尖峰、厚尾特征，还能捕捉到一定的偏态性［7］。更为重要的是，非对称拉普拉斯分布只有两个参数，具有有限的各阶中心矩，有明确的经济意义，计算也比较方便。此外，非对称拉普拉斯分布还具有几何稳定性，即如果日收益率服从非对称拉普拉斯分布，那么周、月收益率也服从非对称拉普拉斯分布，这一点是稳定分布所不具备的。在中国，王建华等运用正态分布、稳定分布、非对称拉普拉斯分布拟合中国股票收益率，得出正态分布不能很好地拟合股票收益率的尖峰、厚尾特征，而稳定分布和非对称拉普拉斯分布都能较好地拟合股票收益率的分布特征［8］。钟法林等运用非对称拉普拉斯分布对三种汇率收益率进行拟合，发现它比正态分布能够更好地描述汇率收益率的尖峰、厚尾、偏态的特征［9］。

目前，国内基于非对称拉普拉斯分布来研究中国股指收益率分布的成果还比较少，在已有的一些文献中，样本区间的选取太窄，使得样本容量较小，研究结论缺乏可信度。为了弥补以往研究的不足，本文选取自开始实施涨跌停板制度以来的1997年5月30日至2012年3月30日沪深两市日、周收盘指数数据，运用非对称拉普拉斯分布进行实证检验。

二、非对称拉普拉斯分布理论

拉普拉斯分布最早是由数学家Laplace提出的，与正态分布相比拥有显著的厚尾特征，在工程科学、质量控制、环境科学、期权定价领域得到了广泛应用。但是，拉普拉斯分布是单参数对称分布，能刻画数据尖峰、厚尾特征，但不能描述数据偏态特征，因此Kozubowski T．等把拉普拉斯分布推广到非对称情形，提出了非对称拉普拉斯分布形式［10］。为了便于开展实证分析，这里先根据有关文献简要介绍非对称拉普拉斯分布和它的基本性质［10－11］。

（一）非对称拉普拉斯分布的定义

（二）非对称拉普拉斯分布的混合表示

设N和Z是独立随机变量，且分别服从标准正态分布和指数分布，则表达式为：

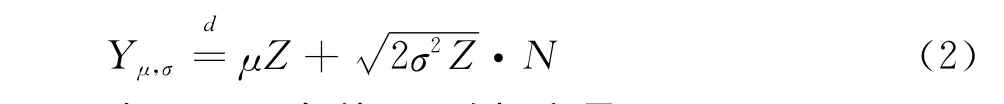
在Z＝z条件下，随机变量Yμ，σ～ AL（μ，σ，κ）服从非对称拉普拉斯分布，其均值和方差分别为μz、2σ2z。

（三）非对称拉普拉斯分布的密度函数和分布函数

表达式（2）在研究非对称拉普拉斯分布中非常重要，由该式可以推导出服从AL（μ，σ，κ）分布的随机变量Yμ，σ与两个服从指数分布的随机变量之差有相同的分布，进而可以通过指数分布密度函数和分布函数很容易得到服从非对称拉普拉斯分布的随机变量Yμ，σ密度函数和分布函数。

若用pμ，σ（x）和Fμ，σ（x）分别表示随机变量Yμ，σ的概率密度函数（pdf）和累计分布函数（cdf），即：

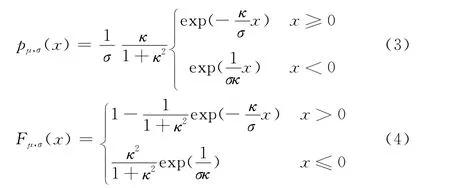
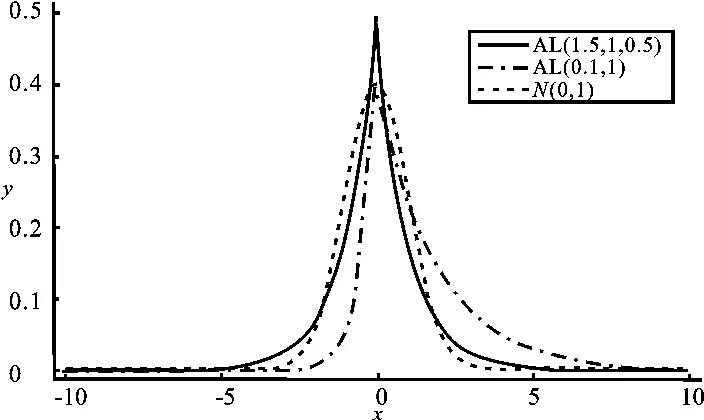
图1 非对称拉普拉斯分布的密度函数图

当μ，σ参数取以下三种情形时，概率密度函数可以简化为以下特殊情形：

（四）非对称拉普拉斯分布的数字特征

由于服从非对称拉普拉斯分布的随机变量Yμ，σ可以由两个相互独立地服从指数分布的随机变量之差来表示，所以它的相关的各阶矩也可以很容易通过相应的指数分布推导出来，结果列于表1。

表1 Y ～ AL（μ，κ，σ）分布的矩

（五）非对称拉普拉斯分布参数的极大似然估计

若Y1，Y2，…，Yn是独立同分布服从AL（μ，σ，κ）分布的简单随机样本，则非对称拉普拉斯分布的似然函数为：

三、中国股指收益率的分布实证检验

（一）数据来源

本文利用沪深两市股指日、周收益率数据，对非对称拉普拉斯分布进行实证检验。上证指数选取日、周收盘综合指数，深证指数选取日、周收盘成分指数。考虑到中国股票市场自1996年底开始实施的涨跌停板制度对股指收益率以及波动性的深刻影响，为了使数据具有可比性，样本区间统一选取为1997年5月30日至2012年3月30日的日、周收盘指数。日收盘指数共计3 593个样本，周收盘指数共计744个样本。数据来源于万德（wind）数据库。记｛Pt，t＝1，2，3，…｝为股指日、周收盘指数序列，其股指收益率序列采用具有良好统计特征自然对数形式表示：

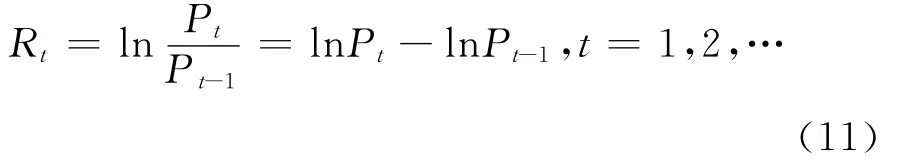
其中｛Rt，t＝1，2，…｝表示日、周股票指数收益率序列。

（二）样本数据的描述统计量

利用已观测到的数据作为样本，计算出沪深两市股指日、周收益率的描述统计量结果列于表2。

表2 沪深两市股指日、周收益率的描述统计量和参数估计值表

从表2可以看出，在偏度方面，无论是上证指数，还是深证指数；无论是日收益率，还是周收益率，均表现右偏。在峰度方面，无论日收益率，还是周收益率，都大于正态分布的峰度3，表现尖峰特征，同时，可以看出日收益率峰度要大于周收益率峰度。

（三）样本数据的正态性检验

从以上描述统计量大致可以看出，沪深两市股指日、周收益率不服从正态分布，为了进一步检验本文的判断，对样本数据进行正态性偏度 — 峰度检验，检验结果列于表3。

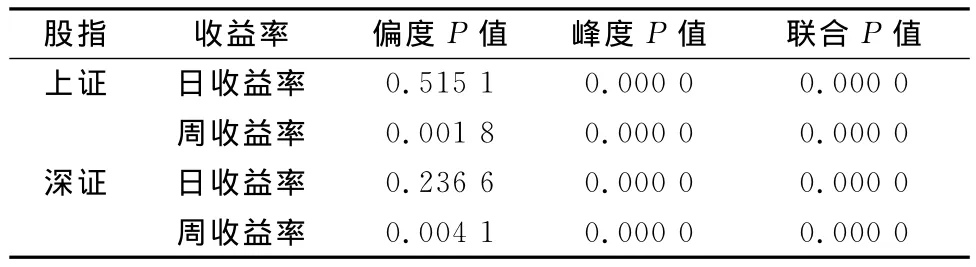
表3 沪深两市股指日、周收益率的正态性偏度与峰度检验表

从检验的结果可知，在1%的显著性水平下，沪深两市股指周收益率无论从偏度还是从峰度考察，抑或是把两者结合在一起考察都表现显著的非正态性。尽管在1%的显著性水平下，沪深两市股指日收益率的偏度（上证P ＝0．515 1，深证P ＝0．236 6）与正态分布的差距不显著，但峰度（P＝0．0000）则是非常显著的，当把两者结合在一起考虑时，同样表现出显著的非正态（P＝0．0000）。因此，可以得出沪深两市股指日、周收益率均不服从正态分布的结论。此外，本文还对此样本进行了Kolmogorov－Smirnov正态检验，结果也和正态性的偏度—峰度检验一致。限于篇幅，检验结果在此省略。

（四）基于非对称拉普拉斯分布估计参数的理论值和经验值

根据拉普拉斯分布参数的极大似然估计量公式（9），分别计算沪深两市股指日、周收益率的分布参数和，列于表2。进一步，将它们代入表1中非对称拉普拉斯分布总体矩的理论值公式，即可得到沪深两市非对称拉普拉斯分布数字特征的理论值。再运用样本矩的公式，可以得到其数字特征的经验值。计算结果列于表4。

表4 基于非对称拉普拉斯分布拟合模型的收益率分布特征理论值和经验值表

从表4可以看出，沪深两市指数日、周收益率偏度、峰度的理论值与经验值都比较接近，这说明应用非对称拉普拉斯分布去拟合沪深两市指数的日、周收益率的分布是合适的。另外，日收益率理论值比周收益率理论值更为接近经验值，说明日收益率的拟合效果要比周收益率的拟合效果好。

（五）非对称拉普拉斯分布的拟合图

为了更直观地呈现股指收益率序列的分布形态及其拟合效果，使用Stata12．0软件绘制沪深两市股指收益率的直方图，并根据相应的估计参数，分别绘制非对称拉普拉斯分布和正态分布的密度函数图，并把它们叠加在一起，形成如下拟合图2～5。

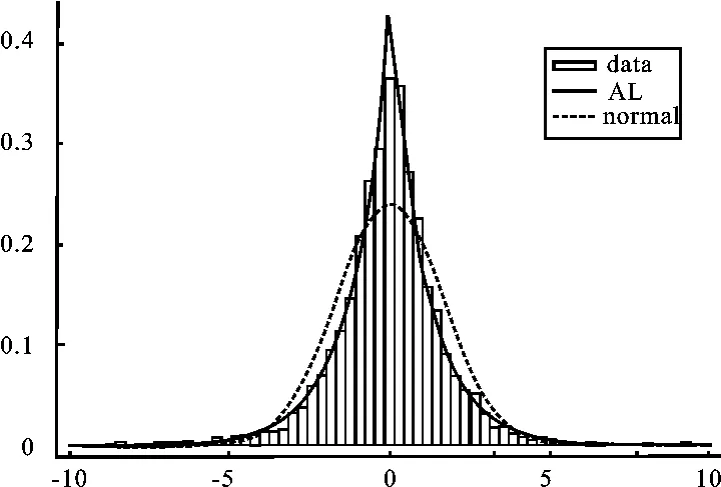
图2 上证股指日收益率的分布拟合图

从拟合图2～5也可以看出，非对称拉普拉斯分布能较好地拟合沪深两市股指日、周收益率分布，比正态分布的拟合效果好，且图形也直观显示出沪深两市日收益率分布拟合效果优于周收益率。

（六）非对称拉普拉斯分布拟合优度检验

为了进一步证实上述结论，运用Kolmogorov－Smirnov拟合优度检验。D为分布函数和样本累积分布函数之间的K－S最大距离，用来检验样本数据是否服从非对称拉普拉斯分布。检验结果见表5。

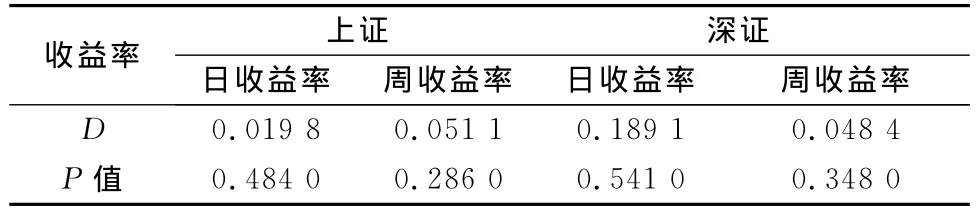
表5 非对称拉普拉斯分布K－S拟合检验

从表5可以看出，基于非对称拉普拉斯分布的沪深两市股指收益率拟合检验P值均远大于5%，不能拒绝原假设，即可以认为沪深两市日、周收益率序列服从非对称拉普拉斯分布。

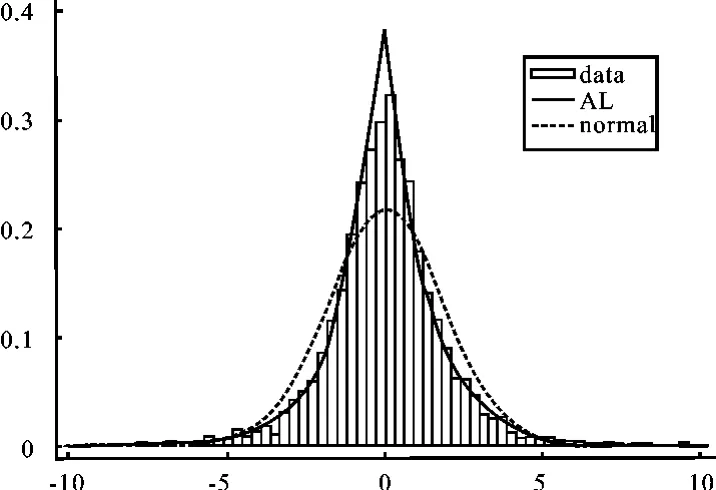
图3 深证股指日收益率的分布拟合图

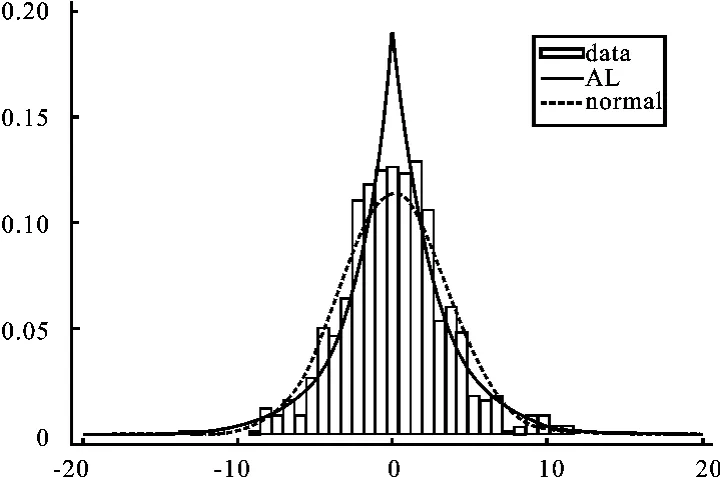
图4 上证股指周收益率的分布拟合图

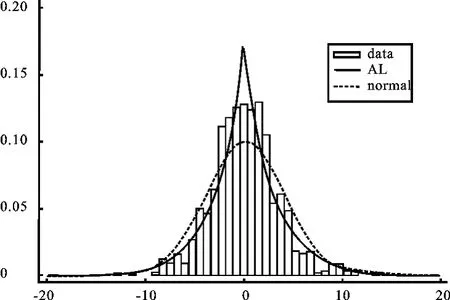
图5 深证股指周收益率的分布拟合图

四、结 论

综上所述，研究结果表明：非对称拉普拉斯分布能够比正态分布更好地反映两市股指日、周收益率数据的尖峰、厚尾、偏态特征，且日收益率分布的拟合效果要优于周收益率的拟合效果。由于非对称拉普拉斯分布有显性的表达式，具有有限的各阶中心矩，比较便于开展参数估计和数字特征的计算。在实践中，可以基于拟合的非对称拉普拉斯分布来计算股指收益率的VaR、CVaR，因此对于股指期货投资者而言，在进行尾部风险测量时，非对称拉普拉斯分布将是较好的选择。

［1］ Kendall M．The Analysis of Economic Time Series［J］．Journal of the Royal Statistical Society，1953，96（1）．

［2］ Osborne．Brownian Motion in the Stock Market［J］．Operations Research，1959，10（2）．

［3］ Mandelbrot B．The Variation of Certain Speculative［J］．Journal of Business，1963，36（1）．

［4］ Fama E F．Mandelbrot and the Stable Paretian Hypothesis［J］．Journal of Business，1963，36（4）．

［5］ 徐龙炳．中国股票市场收益稳态特征［J］．金融研究，2001（6）．

［6］ 王建华，王玉玲，柯开明．中国股票收益率的稳定分布拟合与检验［J］．武汉理工大学学报，2003（10）．

［7］ Kozubowski T，Podgorski K．Asymmetric Laplace Laws and Modeling Financial Data［J］．Mathematical and Computer Modeling，2001，34（2）．

［8］ 王建华，柯开明，王玉玲．非对称拉普拉斯分布在股票收益率中的应用［J］．武汉理工大学学报，2004（3）．

［9］ 钟法林，陈荣达．非对称Laplace分布下外汇收益率的实证分析［J］．吉林工商学院学报，2011（7）．

［10］Kozubowski T，Podgorski K．Asymmetric Laplace Distribution［J］．Mathematical Scientist，2000，25（1）

［11］Kotz S，Kozubowski T，Podgorski K．The Laplace Distribution and Generalizations［C］．Boston Birkhauser：A Revisit with Applications to Communications，Economics，Engineering，and Finance，2001．

An Empirical Study on Asymmetric Laplace Distribution of Stock Index Returns in China

ZENG Wu-yi，LIU Fei
（School of Economics，Xiamen University，Xiamen 361005，China）

The paper fits daily and weekly stock index return data in Shanghai Composite Index and Shenzhen Component Index using asymmetric Laplace distribution．It concludes that asymmetric Laplace distribution is better fitted than normal distribution about the characteristics of leptokurtic，heavy tail，skewness．And the daily return is better fitted than weekly return．When we choose the distribution for calculating VaR and CVaR on stock index return，asymmetric Laplace distribution will be a better choice for stock index risk manager．

asymmetric Laplace distribution；stock index returns；leptokurtic；heavy tail

F810

A

1007－3116（2012）12－0027－05

2012－08－29；修复日期：2012－09－19

曾五一，男，福建泉州人，教授，博士生导师，研究方向：国民经济统计，统计理论与方法；

刘 飞，男，安徽阜阳人，博士生，研究方向：金融时间序列，风险管理。

（责任编辑：崔国平）