类铍离子磁偶、磁四和磁八光谱跃迁的理论研究

易有根, 何 花, 江少恩, 郑志坚, 唐永建



类铍离子磁偶、磁四和磁八光谱跃迁的理论研究

易有根1, 何 花1, 江少恩2, 郑志坚2, 唐永建2

(1. 中南大学 物理与电子学院, 湖南 长沙, 410083; 2. 中国工程物理研究院 高温高密度等离子体物理国家重点实验室, 四川 绵阳, 621900)

采用全相对论量子力学GRASP2程序和平均能级AL模型, 在核的有限体积效应、Breit和QED效应的高阶扰动基础上, 系统地计算了类铍离子组态磁偶极1、磁四极2和磁八极3光谱跃迁波长, 跃迁几率和振子强度, 所得结果和最近的实验数据及理论计算值进行了比较, 结果表明: 高原子序数的高荷电离子的磁多级矩的跃迁几率和中性原子的电偶极矩相当, 在ICF和MCF高温激光等离子体中, 磁多级矩的跃迁几率过程不能被忽视.

高剥离态; 类铍离子; 能级间隔; 跃迁几率; 振子强度

由于磁多极矩光谱跃迁[1-3]在天体物理、X-ray射线激光以及受控惯性约束热核聚变等领域的重要应用, 其越来越受到科技工作者的高度重视, 虽然这些跃迁过程相对电偶极矩跃迁E1而言是禁戒的, 但由于受控惯性约束热核聚变粒子能量极高, 离子处于各种各样的电离态, 故在天体物理、X-ray射线激光以及受控惯性约束热核聚变等领域, 高元素高剥离态的磁多极矩禁戒跃迁一直被用于原子的束薄光谱学和太阳日冕X-ray分析, 物理学家对这些磁偶1、磁四2和磁八3极矩跃迁一直表示出相当浓厚的研究兴趣[4-5]. 在激光高温等离子体的诊断过程中, 这些磁偶极1、磁四极2和磁八3极矩光谱跃迁可为激光惯性约束受控热核聚变在托克马克装置中研究高温高密度等离子体物理现象的过程提供一种有效的诊断工具.

类铍离子磁偶极1 1s22s2p3P1-1s22s2p3P2和1s22s2p3P0-1s22s2p3P1光谱跃迁已有一些报道, Lawson等[6]测量了磁偶极1高剥离类铍钛离子1s22s2p3P1-1s22s2p3P2光谱跃迁线波长; Hinnov等[7]观察到了磁偶极1类铍铁离子和类铍铜离子1s22s2p3P1-1s22s2p3P2光谱跃迁线波长; Perger 等[8]采用多组态Dirac-Fock方法和Edlen等采用半经验方法对高剥离类铍离子磁偶极11s22s2p3P1-1s22s2p3P2光谱(= 4—32)的能级结构间隔进行过理论上的计算. 对类铍离子磁四极2 1s22s21S0-1s22s2p3P2光谱跃迁, 却鲜有报道, 仅在理论上采用相对论多组态Hartree-Fock方法或相对论多体微扰RMBPT方法, 而对类铍离子磁八极矩33s3p3P2-3s3p1P1几乎没有任何报道. 总之, 对离化程度比较高的中等和高元素的类铍离子磁偶极1、磁四极2和磁八极3矩跃迁光谱极少见有关文献作出相应的报道.

铁是等离子体过程中产生的杂质之一, 但铁元素的光谱特征却频繁用于等离子诊断. 因此, 为了跟踪完成等离子诊断过程, 对所涉及的这些特定杂质元素的光谱知识详细了解就显得尤为重要. 对中等值和高离化值荷电离子, 其电子关联效应占有十分重要的地位. 相对论效应对离化值高荷电离子也不可以忽略, 采用全相对论量子力学处理则变得更为贴切[9-10]. 本文根据相对论多组态理论的程序GRASP2, 系统计算了高离化类铍离子磁偶1、磁四2和磁八3极矩跃迁, 计算结果表明: 在原子序数低值时磁偶1、磁四2和磁八3光谱跃迁能级间隔就会在可见和红外光谱区域, 相对来讲, 它们之间则具有较低的跃迁几率, 反之, 在较高的原子序数值时其光谱跃迁能级间隔就会转移到紫外光谱区域, 相对而言, 它们之间则具有较高的跃迁几率. 这些谱线常常用于激光等离子温度和密度的诊断.

1 基本理论与方法

在相对论多组态Dirac-Fock理论中[11-16],电子原子或离子体系的Hamiltonian量为:

第个电子的Dirac-Coulomb Hamiltonian量, 它由式(2)给出:

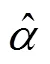
考虑到能量函数和径向波函数有关, 得到了相对论自洽场方程如下:

径向波函数nk() 和nk() 可以用自洽场迭带方法通过求解径向Dirac方程得到, 以Breit修正和量子电动力学效应修正(包含自能和真空极化能)作为微扰, 可得到能量和波函数的高阶近似. 对具体的平均能级AL方法, 优化加权对角哈密顿矩阵元得到能量函数:

根据含时微扰理论, 单位时间内(0= h3/(e4))从上能态|′′′ >到所有低能态|>的爱因斯坦自发辐射的跃迁几率为:

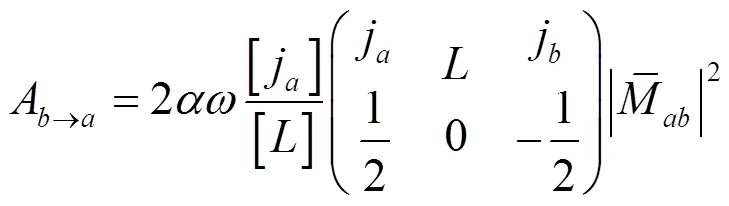
单位时间内从原子态Г到Г原子态的光谱线跃迁的振子强度为:

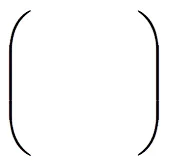
2 计算结果与讨论

计算中采用平均能级模型(AL), 并选取2参数费米(Fermi)和有限核电荷分布, 考虑了Breit 修正, QED 修正和核的体积效应, 自洽场迭代精度一般优于10-8, 选取3个电子组态1s22s2p, 1s22s2和1s22p2. 这3个电子组态可以耦合出10个组态状态波函数CSF, 用这10个组态状态波函数来构造原子的状态函数ASF. 表1-表3中分别列出了采用的3组态对类铍离子组态磁偶极1 1s22s2p3P0-1s22s2p3P1, 1s22s2p3P1-1s22s2p3P2, 1s22p23P0-1s22p23P1, 1s22p23P1-1s22p23P2, 磁四极2 1s22p23P1-1s22p23P2, 1s22s2p3P0-1s22p23P2, 1s22s2p3P0- 1s22p21D2, 1s22s2p3P1-1s22p23P1, 1s22s2p3P2-1s22p23P0,1s22s2p3P2-1s22p23P2, 1s22s2p3P2-1s22p21D2, 1s22s2p3P2-1s22p21S0, 磁八极3 1s22s2p3P2-1s22s2p1P1光谱跃迁波长的计算结果, 与实验值以及两者的差别, 跃迁几率和振子强度, 理论计算结果表明: 在计算磁多极矩精细结构能级间隔时, 沿整个等电子序列Breit修正和QED量子电动力学关联效应修正均随着核电荷数的增加而增加. Breit修正和QED量子电动力学关联效应均不能被忽略. Breit修正一般比QED修正大1至2个数量级, 譬如, 对于关于类铍离子磁偶极矩光谱跃迁1 1s22s2p3P1-1s22s2p3P2, 这个Breit修正和QED量子电动力学关联效应修正可以从表4看得出来. 量子电动力学(QED)修正, 一般而言, 都会随着原子核电荷数的增加而增加, 量子电动力学效应在高剥离态高原子就变得比较重要, 尤其是对高元素的高剥离态重离子. 另外, 当原子的核电荷数沿整个等电子序列增加(= 13-92)时, 类铍离子磁偶极1、磁四极2和磁八极3光谱跃迁的精细结构光谱项在原子序数= 32号元素开始从LS耦合过渡到J-J耦合.

表1 类铍离子磁偶极矩M1光谱跃迁波长, 跃迁几率和振子强度 (Z = 13-92)

续表

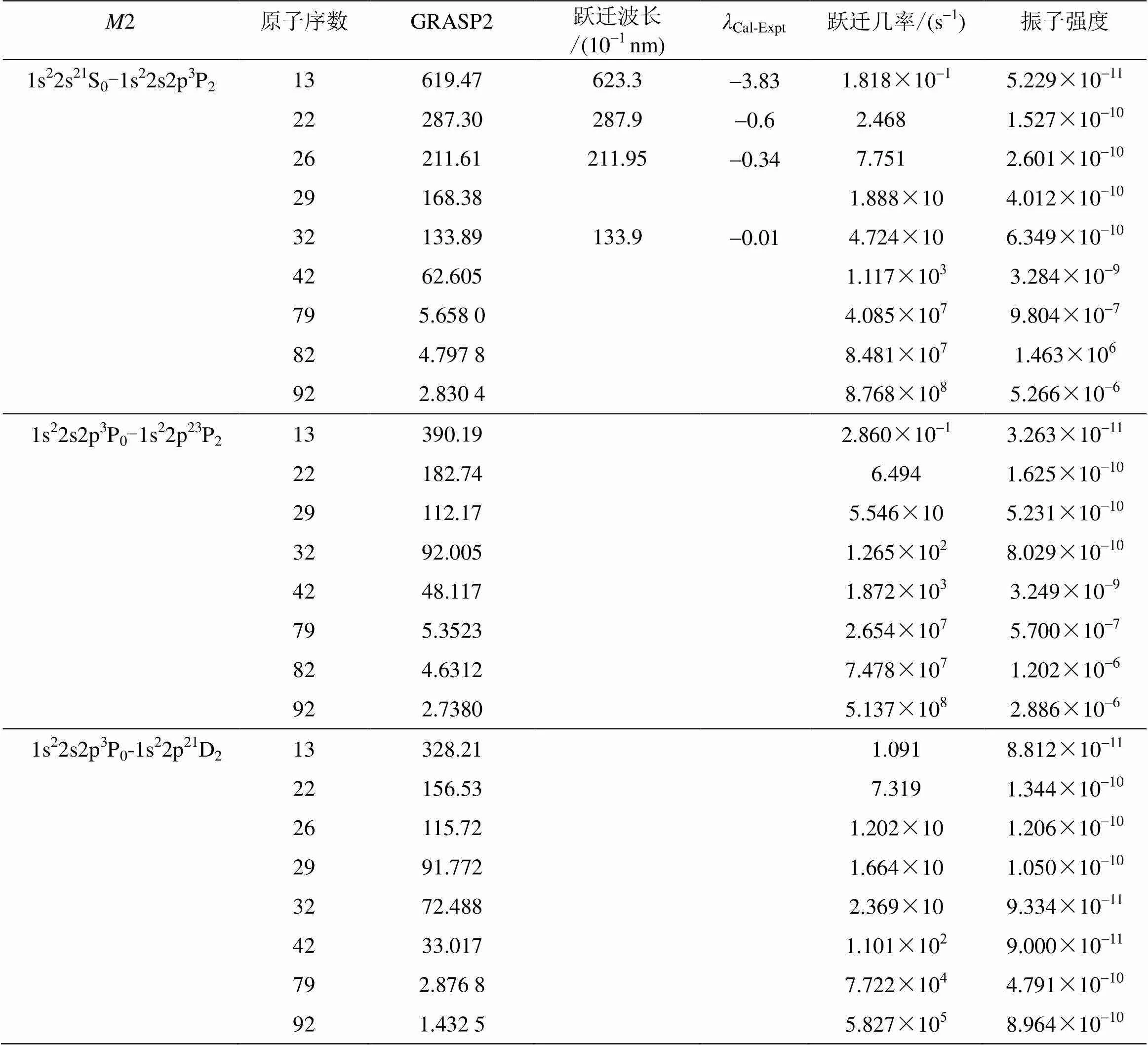
表2 类铍离子磁四极矩M2光谱跃迁波长, 跃迁几率和振子强度(Z = 13-92)

续表

表3 类铍离子磁八极矩3光谱跃迁波长, 跃迁几率和振子强度(= 13-92)

为了直接验证计算数据的可靠程度, 需要考察一下类铍离子磁偶极11s22s2p3P1-1s22s2p3P2光谱跃迁能级结构间隔. 表4给出了类铍离子磁偶极1 1s22s2p3P1-1s22s2p3P2光谱跃迁的Zero-order 相互作用能, Breit修正和量子电动力学QED效应对能级结构间隔的影响. 对高剥离类铍钼、类铍金和类铍铀, 其Zero-order 相互作用能分别为887 518.52 cm-1、16 018 464.15 cm-1和33 311 397.64 cm-1, Breit修正分别为-21 289.14 cm-1、-220 160.10 cm-1和-416 080.50 cm-1, 以及量子电动力学QED效应分别为1 795.70 cm-1、16 735.0 cm-1和18 289.0 cm-1. 其中Breit修正分别占总能量的-2.39%、-1.37%和–1.24%, QED量子电动力学关联效应分别占总能量的0.20%、0.10% 和 0.05%. 虽然沿整个等电子序列谱线Breit修正和QED修正所占的百分比在减少, 但Breit修正和QED修正能的绝对值却在增大. 另外, 从增加的电子组态角度来考察, 增加的电子组态对能级间隔的影响并不十分明显, 这主要是由于增加的电子组态1s22s2和1s22p2的宇称和1s22s2p的宇称相反. 在平均能级模型(AL)计算中, 只有增加相同宇称的电子组态才能对结构能级间隔产生影响, 因为单粒子轨道是由能量函数的最小值所决定. 关于平均能级模型(AL)的更加深入的讨论参见相关文献.

表4 类铍离子磁偶极矩M1 1s22s2p3P1-1s22s2p3P2光谱跃迁Breit效应 QED修正对能级间隔的贡献 (Z = 13-92)

为了和实验数据和其它理论计算值作出更为详细的比较, 表5给出了Cheng[7]和及GRASP2的理论跃迁能级间隔11s22s2p3P1-1s22s2p3P2计算值、Edlen 的半经验值、一些光谱实验值和参考数据. 从表5中可以清楚地看出, 本文的结果比MCDF方法的工作稍好一点, 尤其是在低元素区域, 这是由于本文的计算方法中考虑到了量子电动力学的高阶效应. 结果和Cheng不一致主要是由于Cheng采用了每个能级分别由自洽场计算单独决定的优化能级(OL)模型, 目前的GRASP2计算结果和Edlen算值均比实验值稍小. 其磁偶极11s22s2p3P1-1s22s2p3P2精细结构间隔的误差在千余个波数范围之内, 目前的GRASP2理论结果与实验结果的误差大约在0.4%～0.5%.

表6 列出了类铍离子磁四极2 1s22s21S0-1s22s2p3P2光谱跃迁的能级间隔的理论计算值, 文献值和实验数据, 我们不难看出, 目前的计算结果和实验结果实现了基本一致, 与MCDF+MZ[13]和RMBPT[13]方法的计算值也吻合得比较好. 理论计算值与实验数据的偏差主要取决于电子关联能和相对论效应, 对于低元素的剥离离子, 偏差主要是由于电子关联能的影响, RMBPT方法采用冻实计算原子中相应电子组态的能量, 但是他们并没有充分考虑原子实内电子产生的关联能的相互作用, 如果离子的离化程度比较高, 或离子处于高元素的剥离状态, 发生在电子之间的屏蔽效应必将造成不同的相互作用模型势引起不同的量子力学QED的关联能修正, 用冻实二阶关联的RMBPT方法可进行很好的量子电动力学关联修正, RMBPT方法更接近实验值. 目前的GRASP2理论结果与实验结果的误差大约在0.08%～0.6%.

表5 类铍离子磁偶极矩M1光谱跃迁能级间隔和实验值及其它理论值的比较 (Z = 13-92)

表6 类铍离子磁四极矩M2光谱跃迁能级间隔和实验值及其它理论值的比较 (Z = 13-92)

以类铍离子磁偶极矩11s22s2p3P1-1s22s2p3P2光谱跃迁和实验数据及其它理论计算结果作一比较, 表7给出了类铍离子磁偶极矩11s22s2p3P1-1s22s2p3P2光谱跃迁的自发跃迁几率的实验值、GRASP2以及Lorenzo J Curtis[7]的自发跃迁几率的理论计算值.

从表7中可以发现, 本文的计算结果和Lorenzo J Curtis 等用经验光谱数据(empirical spectroscopic data)方法及多组态自洽场(Multi-configuration Dirac-Fock)方法计算的跃迁几率值很好地符合. 对有实验的光谱数据而言, 譬如, 高离化类铍铜离子、类铍氪离子的自发爱因斯坦系数和实验光谱数据值基本一致. GRASP2的理论计算类铍离子磁偶极矩11s22s2p3P1-1s22s2p3P2光谱跃迁的自发跃迁几率的结果与实验之间的误差大约2%, 表1-表3清楚地表明沿整个等电子序列磁偶极矩1光谱跃迁的自发跃迁几率在10～1011之间变化. 在原子序数为= 92时, 自发跃迁几率高达1011, 磁四极矩2光谱跃迁的自发跃迁几率在10～109之间变化; 在原子序数为= 92时, 自发跃迁几率高达109, 磁八极矩3光谱跃迁的自发跃迁几率在10-8~10-6之间变化; 在原子序数为= 92时, 自发跃迁几率为10-6.

表7 类铍离子磁偶极矩光谱跃迁几率(s-1)和实验值及其它理论值的比较 (Z = 13-92)

表8 列出了类铍离子磁四极2 1s22s21S0-1s22s2p3P2光谱跃迁的能级之间的跃迁几率的理论计算值、文献参考值和实验数据. 从表8中可以看出, 目前的计算结果和MCDF结果基本一致, 与其它的计算值也吻合得比较好. 实验数据极少, 目前仅有Glass[1]测量了铁元素的2 1s22s21S0-1s22s2p3P2的跃迁几率, 与本文的计算结果吻合很好. 理论计算值与实验数据的偏差, 对于低元素的剥离离子主要取决于原子实内部用电子组态计算的关联能, 对于高元素的剥离离子, 主要取决于相对论效应, 采用不同的模型势能函数, 由于电子间的屏蔽效应, 造成包含自能和真空激化能在内的量子电动力学QED关联能修正也会具有不同的特征.

表8 类铍离子磁四极矩光谱跃迁几率和实验值及其它理论值的比较 (Z = 13-92)