小波变换与HMT模型的图像插值算法*
2012-05-09郭昌
郭 昌
(安徽大学电气工程与自动化学院,安徽 合肥 230601)
由Crouse等提出的小波域隐Markov模型,又称为隐Markov树(HMT)模型,将图像的小波系数建模为隐马尔可夫树模型,该模型考虑了小波系数间的统计相关性及非高斯性,抓住了小波系数的本质特性和小波系数间的主要关系,在图像去噪、压缩、边缘检测和识别等图像处理领域中取得了很好的效果[1]。
本文研究了一种基于小波变换与隐马尔可夫模型相结合的图像插值方法。小波域HMT模型采用混合高斯模型刻画各子带系数的概率分布[2],并通过小波系数隐状态在多个尺度之间的Markov依赖性来刻画原始图像小波系数随尺度减小而指数衰减的特性。由于小波域 HMT 模型准确刻画了原始图像小波变换的统计特性,本文算法以此作为原始图像的先验模型,将图像插值问题转化为一个约束优化问题。实验结果表明,基于小波域HMT模型的图像插值算法改善了传统插值算法引起的锯齿效应和平滑效应,插值后的图像中细节丰富,无明显的畸变。
1 小波域隐马尔可夫树模型
HMT模型与小波系数的持续性相匹配,通过把小波系数的边缘概率密度函数建模成具有隐状态的混合高斯分布来捕获相邻尺度间的小波系数的相关性。这个隐状态决定该系数是大或是小,并由概率树来描述状态之间的马尔可夫依赖性。 该树状结构将每个小波系数的状态变量同它的下一层的四个子节点的状态变量相连,它和DWT的小波系数一样具有相同的四叉树拓扑结构。如图1所示,其中实心黑点表示小波系数,空心白点表示小波系数所处的状态。小波分解的每个通道都用它自己的四叉树来描述,各通道之间相互独立。从图中可以看出,HMT的Markov结构是建立在小波系数ω1的状态上的,而不是建立在小波系数上[1,3]。
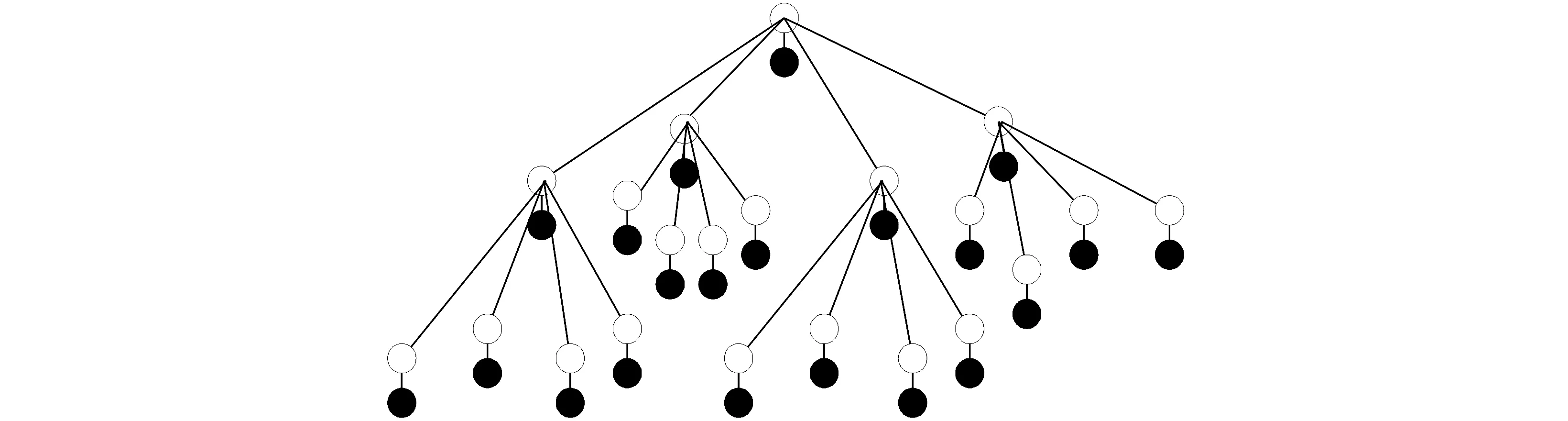
图1 小波系数及其状态的四叉树模型
HMT模型还描述了小波系数间的相关性。小波系数的延续表明沿着尺度方向的小波系数(父子系数间) 具有较强的相关性,对每一个通道,用父系数的状态变量和其子节点系数的状态变量相连的概率树来描述其相关性,和小波系数一样,每通道得到一个四叉树。具体说,父状态到子状态的连接关系用状态转移矩阵A表示[4-5]:
(1)
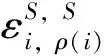

1)独立混合高斯分布。如果已知第i个结点小波系数状态的概率,则小波系数ωi的概率密度与其他小波系数及状态无关。即
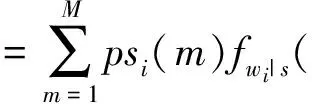
(2)

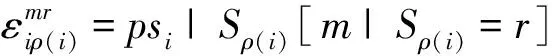
上述有关参数加上根结点的状态概率psi(m)构成了HMT模型参数,记为θ。模型参数θ可以由EM算法得到。如果已知小波系数W和模型参数θ,我们还可以通过Upward-Downward 算法。计算小波系数的后验状态概率p(Si=m|W,θ)。
3)小波系数的联合概率分布。假定图像小波变换的三个通道相互独立,则小波系数的联合分布。
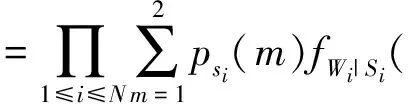
(3)
其中,W表示小波系数全体,N为小波系数个数[3]。
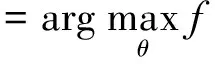
(i)选择初始模型参数θ0,置计数器l=0;
(ii)E步:计算隐状态变量的联合概率p(S|W,θ);
(iii)M步:更新模型参数
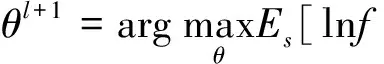
(iv)θl=θl+1,若满足收敛条件则停止,否则转(ii)。
理论证明EM算法通过E步、M步的交替迭代最终收敛于不完全似然函数f(W|θ)的一个局部极大值[6-8]。
EM算法是由不完全学习数据(因为隐状态未知)估计模型参数的有效且常用的方法,其每一迭代步的计算复杂度为O(n)(n=N×N),但算法的收敛是耗时的,如果能从合适的模型参数开始学习,则学习时间会大大缩短。通过分析发现可以找到比较合适的参数初值。
首先小波系数随着尺度的增加(分辨率增加)具有指数衰减性,由于HMT将小波系数建模为具有隐状态的混合高斯分布,混合方差的值也反映了小波系数的值,因此小波系数的指数衰减性表明方差在尺度间也具有指数衰减性,在初始化时应将此反映出来。
2 基于小波域 HMT模型的图像插值
由于HMT模型结合了小波变换和多尺度Markov模型,能很好地刻画小波系数的统计特征,目前在图像去噪应用中已经取得了很好的效果,因此本文将其应用在了图像插值中,提出了一种基于小波域 HMT模型的图像插值方法,其算法流程图如图2所示。
因此小波域 HMT插值过程是首先对原始低分辨率图像进行小波分解,然后利用小波域HMT模型对小波系数进行重新估算,再进行小波逆变换得到经过插值的高分辨率图像。
通常,对于图像插值问题的求解是构造一个前向关系模型[9],如果不考虑非线性因素的影响,低分辨率图像和高分辨率图像的关系可以由下述数学模型描述:
gk=MHjNj,kfj+ξj, 1≤j,k≤n
(4)
(4)式中:j、k为图像序列的帧数,fj为待求的第j帧高分辨率图像,gk为第k帧观察到的低分辨率图像,ξj为采样过程中Gibbs现象产生的噪声。矩阵M为下采样过程,Hj为模糊矩阵,Nj,k为第j帧和第k帧之间运动矢量所构成的运动矩阵。
如果设D=MHjNj,k,且忽略噪声的影响,则式(4)即可以简化为
gk=Dfj1≤j,k≤n
(5)
因此只要能够求解出矩阵D然后进行逆变换即可得到经过插值的高分辨率图像。
首先对低分辨率图像gk进行小波分解,由此将分解得到的小波系数与HMT匹配,以得到小波系数的HMT模型,再将这一模型看成先验信号分布。为了将得到的小波系数与HMT匹配,采用EM算法。
在完成HMT参数估计后,可直接估算插值图像的参数,由此得到插值图像fj的小波系数状态后,通过小波逆变换就可以得到插值放大的图像。
实验结果表明,经过上述算法得到图像中,我们发现插值图像后很容易现诸如Gibbs现象之类的情况,主要表现为振铃和锯齿,即在图像的某个区域出现类似水波一样的皱纹,产生这种现象是由于小波变换不具有平移不变性造成的。由于小波变换的局部化特征,其振荡幅度与奇异点的位置有很大的关系。在奇异点的邻域内,经过正交小波变换分解后的图像会表现出Pseudo-Gibbs现象,其经过小波重构回来的插值图像在奇异点附近交替出现较大的上、下峰值,这些峰值并不是原始信号本身包含的,而是在插值过程中产生的人为干扰[10]。这种现象类似于基于Fourier去噪产生的Gibbs现象。
3 试验结果与分析
为了验证本文提出的插值方法的效果,我们对传统插值方法和本文所提出的基于小波变换的图像插值方法进行试验。为验证本文算法的先进性与正确性,采用峰值信噪比来评价效果的好坏。其方法就是先把一幅512×512的图像与式(6)的3×3矩阵作卷积[3],然后隔点取样得到一幅256×256的原始图像,然后通过对这幅256×256的图像进行插值处理,得到放大4倍插值后的图像,再定量分析放大图像与原始图像之间的差别。
(6)
值得注意的是,采用不同的方法对图像进行缩小对结果也是有影响的:一是要考虑边缘效应问题,二是有些方法会使缩放前后的图像在中心点上不能严格对齐。
由于图像插值的目的不同,对插值方法的评价标准也不同。但是,图像插值目的主要有两个:①恢复图像的真实面貌,保持图像的纹理、边缘等细节信息。②改善图像的视觉效果,便于人眼更好的观察与分析图像Limb通过研究发现,在各种客观质量评价形式中,峰值信噪比是一种比较接近人眼视觉效果的一种客观评价。为此,我们采用峰值信噪比作为评价标准。
实验采用的图像为两幅遥感图像,人物Barbara,采用的方法为常见的三种插值方法:最近邻插值、双线性插值和双三次插值与本文提出的方法做对比试验。测得数据如表1、表2所示。
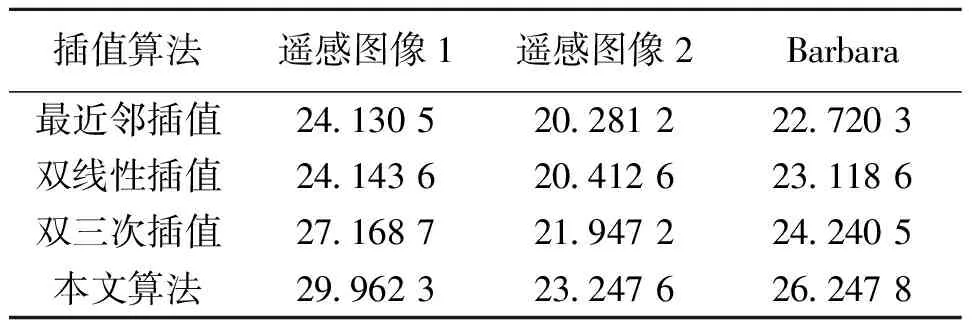
表1 峰值信噪比
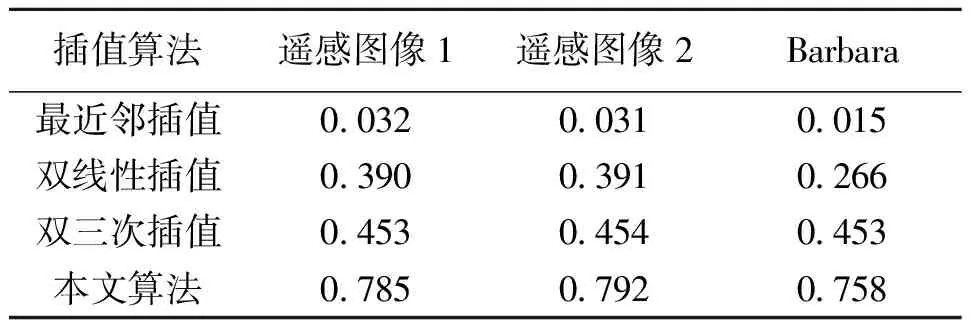
表2 插值所用时间
由试验结果分析。从主观上,本文算法插值图像的视觉效果良好,如图3、图4、图5所示,能够清晰的分辨出图像中的细节,没有出现传统算法的锯齿效应和平滑效应;从客观上,测得的实验数据表1中显示峰值信噪比得到了明显的提高。结合表2数据分析随着算法的复杂性提高,本文算法在耗时上略微增加,但在可以接受的范围内。本文算法在遥感图像、人物图像上具有通用性。
4 结 论
本文提出的图像插值算法以小波域HMT模型描述自然图像小波变换的统计特性,并以此作为原始图像的先验模型,把图像插值问题表述为一个约束优化问题。该方法能够较好的保持原图像中丰富的高频信息,经插值处理并小波重建后的图像主观上具有很好的视觉效果,客观上具有较高的峰值信噪比,并且图像中细节丰富,无明显的畸变,实验结果表明该方法是超分辨率图像处理的一种行之有效的途径。但算法的效率需要在以后的研究工作中进行改进。在遥感图像、人物图像上插值的对比实验表明了新方法的有效性与广泛的应用性。

图3 遥感图像1

图4 遥感图像2

图5 Barbara图像
参考文献:
[1]汪西莉,刘芳,焦李成.一种小波域HMT模型参数初始化方法[J].计算机科学,2003,30(1): 85-86.
[2]KINEBUCHI K,MURESAN D D,PARKS T W.Image interpolation using wavelet-based hidden Markov trees[C]∥IEEE International Conference on Acoustics,Speech,and Signal Processing,2001,(3):1957-1960.
[3]ZHAO S B,HAN H,PENG S L.Wavelet-domain HMT-based image super-resolution[C]∥IEEE International Conference on Image Processing,2003: II953-II956.
[4]DONG HIM WOO,IL KYN EOM,YOO SHIN KIM.Image interpolation based on interscale dependency in wavelet domain[C]∥IEEE International Conference on Image Processing,2004:1687-1690.
[5]ROMBERG J K,HYEOKHO CHOI,BARANIUK R G.Bayesian tree-structured image modeling using wavelet-domain hidden Markov models[J].IEEE Transactions on Image Processing,2001,10(7): 1056-1068.
[6]RICHARD A REDNER,HOMER F WALKER.Mixture densities,maximum likelihood and the EM algorithm[J].SIAM Review,1984,26(2): 195-239.
[7]浦利,刘玉树,金伟其.基于非均衡系数小波变换的插值算法研究[J].南京理工大学学报:自然科学版,2007,3:323-326.
[8]龙兴明,周静.基于EM算法的图像小波系数统计研究[J].计算机仿真,2005,22(6): 71-74.
[9]ELAD M,FEUER A.Restoration of a single superresolution image from several blurred,noisy,and undersampled measured images[J].IEEE Transactions on Image Processing,1997,6(12): 1646-1658.
[10]DONOHO D L,JOHNSTONE I M.Ideal spatial adaptation by wavelet shrinkage[J].Biometrika,1994,81(3): 425-455.
