单位圆周上同胚映射的逆扩张*

李淑龙， 刘学文

(1.南方医科大学生物医学工程学院，广东 广州 510515；2.深圳西乡中学新高中部，广东 深圳 518102)

S1上映射的扩张问题已经得到广泛的研究[1-9]，其在Teichmuller空间的研究中具有重要的作用。我们知道：Beurling-Ahlfors扩张不是共形自然的，而Douady-Earle扩张是共形自然的。 由于Beurling-Ahlfors扩张不是共形自然的，它只能直接用于万有Teichmuller空间的研究，而不能直接用于一般的Teichmuller空间的研究。而Douady-Earle扩张是共形自然的，可以直接用于一般的Teichmuller空间的研究。

寻找单位圆周上映射的共形自然扩张是一个很有趣的问题。在本文中我们将定义单位圆周上同胚映射的共形自然扩张——逆扩张,并且我们将通过一个例子证明逆扩张不同于Douady-Earle扩张。

1 主要定义

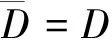
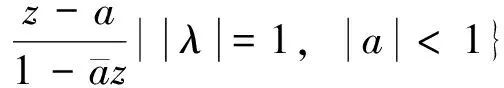
对于每个a，映射

∈G+

满足ga:a→0且0→-a。

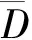
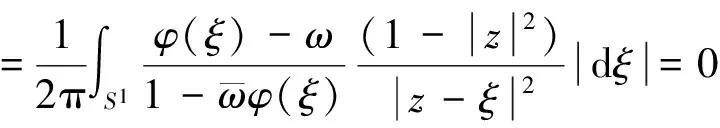
(1)

的唯一解，我们称之为Douady-Earle扩张。 显然F1是定义在D×D上的实解析函数。

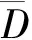
引理2[2]Douady-Earle扩张是共形自然的，即满足

E(gB∘φ∘h)=g∘E(φ)∘h， ∀g,h∈G

易知(1)等价于方程

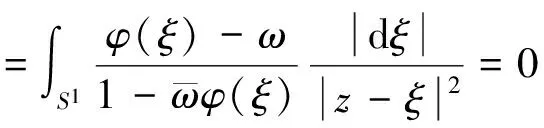
(2)

既然Douady-Earle扩张是共形自然的，不失一般性，我们可以假设E(φ)(0)=0，即

φ(ξ)|dξ|=0或φ(eiθ)dθ=0

(3)

若z∈S1,令z=eiθ,ζ=eit，且ζ=φ(eiθ)=eiψ(θ),则ψ:R→R是同胚映射，且满足ψ(θ+2π)=ψ(θ)+2π。记φ的逆映射为φ-1，则

φ-1(ζ) = eiψ-1(t)

这里ψ-1是ψ:R→R的逆映射，满足ψ-1(t+2π)=ψ-1(t)+2π。

由引理1，我们能够如下定义φ:S1→S1的另一扩张N：

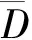
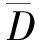
即它是同胚映射φ:S1→S1逆映射φ-1:S1→S1的Douady-Earle扩张映射的逆映射，我们称之为逆扩张。

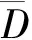
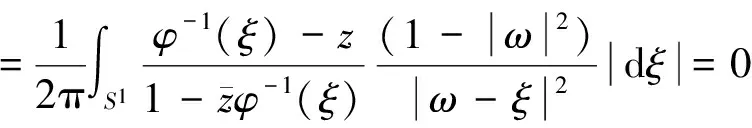
(4)

其等价于

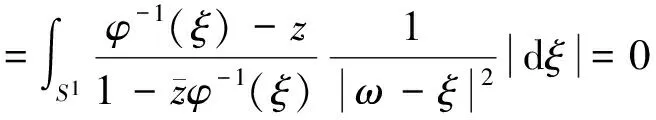
(5)

2 主要定理

假设aj,j=1,2,3是正整数并且满足

(6)

记

我们考虑同胚映射ft:S1→S1如下：对于z=eiθ，

ft(eiθ)=

容易计算

由(3)知上式意味着ωt|z=0=E(ft)(0)=0。 但下面我们将证明

θ≠0，

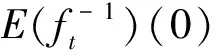
事实上，记ft(eiθ)=eiψt(θ)，那么

ψt(θ)=

(θ)=

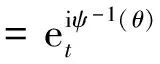
ζθ=

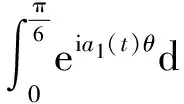
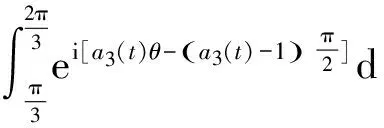
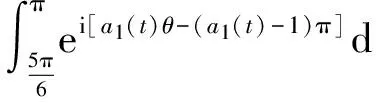
A+B+C-2i

其中

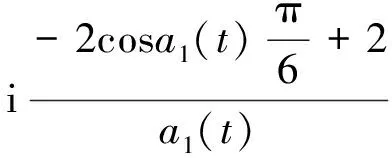
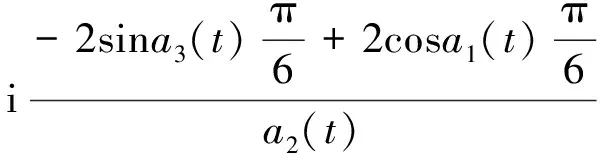
所以

(ζ)|dζ| =A+B+C-2i =

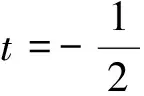
(ζ)|dζ| =A+B+C-2i=

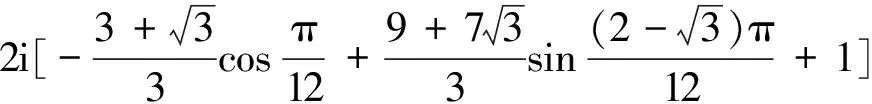
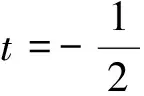
从上面这个例子我们马上有如下定理：

定理1 逆扩张不同于Douady-Earle扩张。

由引理2，即Douady-Earle扩张是共形自然的，同样地逆扩张也是共形自然的。

定理2 逆扩张映射是共形自然的，即满足

G(g∘φ∘h)=g∘G(φ)∘h， ∀g,h∈G

证明∀g,h∈G，

G(g∘φ∘h)=[E((g∘φ∘h)-1)]-1=

[E(h-1∘φ-1∘g-1)]-1=[h-1∘E(φ-1)∘g-1]-1=

g∘E-1(φ-1)∘h

证毕。

参考文献：

[1]李忠.拟共形映射及其在黎曼曲面论中的应用 [M].北京：科学出版社，1988.

[2]DOUADY A,EARLE C J.Conformally natural extension of homeomorphisms of the circle [J].Acta Mathematica,1986,157(1): 23-48.

[3]EARLE C,MARKOVIC V,SARIC D.Barycentric extension and the Bers embedding for asymptotic Teichmüller space [J].Contemporary Math,2002,311: 87-105.

[4]LI S L,LIU L X,SU W X.A family of conformally natural extensions of homeomorphisms of the circle [J].Complex Variables and Elliptic Equations,2008,53(5): 435-443.

[5]FOTIADIS A.Harmonic extensions of symmetric maps [J].Calc Var,2009,35:271-278.

[6]ABIKOFF W,EARLE C,MITRA S.Barycentric extensions of monotone maps of the circle [J].In the tradition of Ahlfors and Bers,III,Contemporary Math,2004,355:1-20.

[7]ABIKOFF W.Conformal barycenters and the Douady-Earle extension|a discrete dynamical approach [J].Anal Math,2002,86: 221-234.

[8]YAO G W.Harmonic maps and asymptotic Teichmuller space [J].Manuscripta Math,2007,122: 375-389.