坝高与弧高比对高拱坝厚高比的影响

2012-05-07方咏来黄朝煊马以超

水利水电科技进展 2012年4期

方咏来,黄朝煊,马以超

(浙江省水利水电勘测设计院,浙江杭州 310002)

拱坝厚薄的度量参数主要有厚高比和柔度系数,厚高比是拱坝底厚与坝高之比,第2版《水工设计手册》[1](2011年出版,以下简称《手册》)对拱坝厚高比与弧高比进行了统计分析,得出了线性关系建议式。柔度系数 C是国际著名坝工专家龙巴迪[2]提出的,是反映拱坝厚薄的一个综合参数,龙巴迪认为正常情况下C值为15左右,若混凝土浇筑技术较高,C值也能达到20。但实际工程表明,不少坝高较低的拱坝,C值较大仍能正常运行,因此用柔度系数评价坝体安全性和经济性时,还要注意坝高要素。对于Kolnbrein拱坝坝踵的开裂[3-4],龙巴迪认为是由于拱坝的柔度系数太大(C=17.7,是已建高拱坝中最大的)、坝体设计得太薄造成的。

任青文等[5]假定拱坝力学模型为圆筒的一部分,从强度观点近似给出了拱坝的强度破损曲线C=3.4σ/(Hγw),其中 σ为混凝土容许抗压强度,H为拱坝坝高,γw=ρwg(ρw为水的密度,g为重力加速度);同时从屈曲观点近似给出破损曲线 C=348/H1/3,并认为拱坝坝体的安全性一般是由强度控制的,只有当坝体采用高强度混凝土,使强度破损曲线抬高、接近或超过稳定破损曲线的情况下,才由屈曲失稳控制。

黄朝煊[6]考虑坝高、河谷宽高比等对柔度系数的影响,通过数值分析得到薄高拱坝底厚建议公式,虽然该公式考虑了拱坝纵断面形状的影响,但计算稍显复杂,并认为拱坝柔度系数与河谷形状、宽高比、坝高等因素密切相关。拱坝的宽高比太大或太小都将导致坝体拱梁受力分配的失调,导致坝体应力过度集中,不利于坝体的安全。

饶宏铃[7]认为,现行规范(指 SL 282—2003《混凝土拱坝设计规范》、SD145—85《混凝土拱坝设计规范(试行)》)仅考虑厚高比来划分拱坝的厚薄,实际上仅从悬臂梁的刚度出发,没有考虑拱圈作用,不能反映拱坝受力情况。

徐福卫等[8]考虑河谷的宽高比影响,利用河谷宽高比与拱坝柔度系数的关系得出了拱坝柔度系数的分区图;认为文献[5]的强度破损曲线相对龙巴迪强度破损曲线有了一定的进步,但文献[5]的强度破损曲线只考虑混凝土的抗压强度,而实际工程中拱坝破坏基本上是因为拉应力或剪应力过大而破坏,认为文献[5]的强度破损曲线的合理性也值得商榷。

基于此,本文依据《手册》中的国内外大量已建拱坝的参数,对高拱坝厚高比、底厚建议值等问题进行探讨。

1 高拱坝厚高比的影响因素分析

潘家铮院士在《特高拱坝枢纽分析与重点问题研究》[9]一书的序言中认为,拱坝的安全性与坝高存在非线性关系,即同样200m高的拱坝整体安全,若将坝体结构外形尺寸均同步放大2倍后,变成400m高的拱坝后就不一定安全,因此拱坝的厚高比与坝高存在非线性增函数关系。

弧高比对拱坝厚高比的影响也较大,拱坝的弧高比越大,其拱的作用效果就越弱,由悬臂梁分担的荷载就越大。因此,拱坝厚高比与拱坝的弧高比存在增函数关系。

此外,拱坝坝址河谷形状越接近U形,悬臂梁分担的荷载就越大,拱坝的厚高比也越大。而河谷两岸岩基的地质状况、河谷形状的对称性等也是影响拱坝厚高比的重要因素。

由于拱坝厚高比涉及影响因素多而复杂,本文考虑其中主要因素如坝高的非线性影响、弧高比的影响以及河谷形状的影响,近似给出拱坝厚高比的经验关系式:

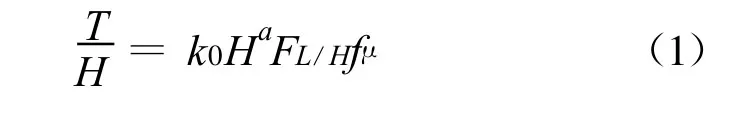
式中:T为拱坝底厚;H为拱坝坝高;k0为河谷两岸岩基的地质状况、河谷形状的对称性等其他因素对拱坝厚高比影响的修正系数,在河谷两岸岩基的地质状况较差、河谷形状不对称等不利因素影响下,k0＞1,具体可参考工程实例;a为待定参数,是坝高对厚高比的影响幂次,可通过统计回归分析法择优选取,a≥0;FL/H为弧高比对厚高比的影响函数,本文分别采用线性回归和抛物线回归分析,依据相关系数择优选取;fμ为拱坝坝址处的河谷形状(U形、V形)对厚高比的影响系数。

由于拱坝实际厚高比的选取涉及影响因素多且复杂,如工程地质条件(两岸及坝基的断层与节理等)、河谷断面形状、坝址处地震状况、坝基渗流状况等,因此,本文通过对已建拱坝资料(表1,取自《手册》))进行统计回归分析,得出拱坝坝高、弧高比等主要因素对拱坝厚高比的影响关系。

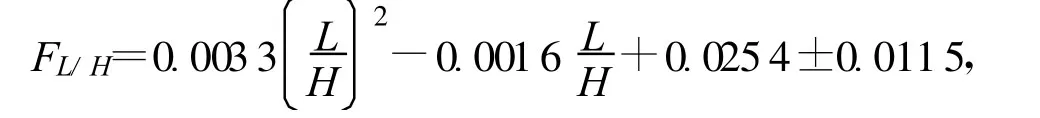
图1 参数a不同取值时厚高比回归分析相关系数

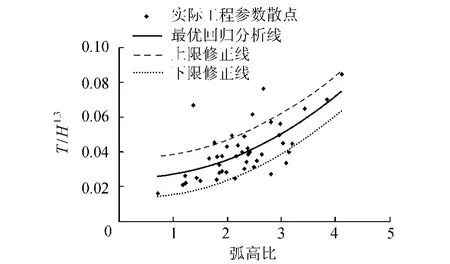
图2 弧高比对厚高比的影响(a=0.3)

[6]中拱坝坝址河谷形状(U形、V形)对厚高比的影响系数,可取参数 fμ=0.9(1+μ),结合式(1)可知拱坝厚高比近似为

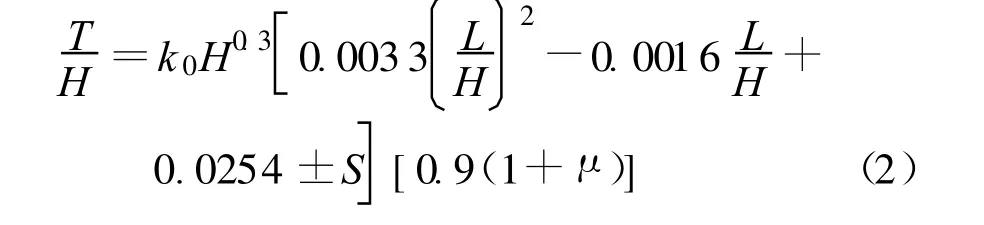
式中:L为坝顶弧长;μ为度量河谷形状的参数,即理想拱坝底部弧长与顶部弧长之比,当为典型U形河谷时 μ=1,而为典型V形河谷时 μ=0,实际拱坝纵断面展开图是很不规则的,若已知拱坝纵断面展开面积A,则 μ可近似取为μ=1;S为标准方差,取 0.0115。

表1 世界上已建拱坝参数及底厚计算值比较

通过比较知,《手册》中厚高比公式是式(2)a=0时的特例。

2 由厚高比导出的拱坝底厚建议公式

《手册》拱坝底厚建议计算公式为

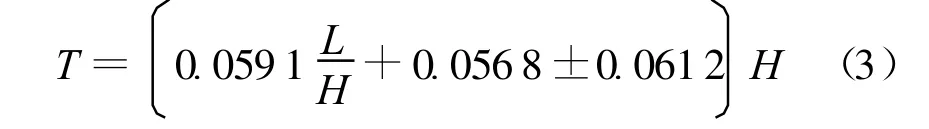
式中:H 为拱冠梁的高度或坝高(《手册》中公式存式在刊误)。

美国垦务局《拱坝设计》[10]建议拱坝底厚采用以下近似公式:

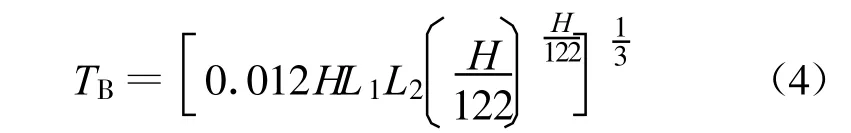
式中:L1为坝顶高程处拱端可利用基岩面河谷宽度;L2为拱冠梁底以上0.15H处拱端可利用基岩面河谷宽度。

根据本文建议厚高比(式(2)),可得拱坝底厚经验公式为

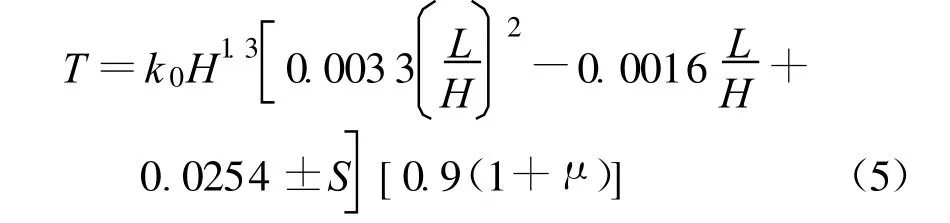
其中标准方差S=0.0115。

对式(3)与式(5)进行计算比较分析(由于资料不全,暂取参数 μ=0.1,k0=1),结果列于表1。由计算结果分析可知,式(5)比式(3)更接近实际设计值,说明式(5)稍优,且由图1可知式(5)的相关系数、标准方差等回归指标均优于式(3),但在特高拱坝中必须考虑河谷两岸岩基的地质状况、河谷形状的对称性等其他因素对拱坝厚高比的修正。

通过计算,认为式(4)对坝高在150m左右的拱坝有参考价值,但对于坝高在300m左右的拱坝计算的建议底厚值太大,没有参考价值。