卡尔曼滤波在落点偏差预测算法中的应用

张永伟，杨锁昌，张 敏，冯继伟

（1.军械工程学院导弹工程系，河北 石家庄 050003；2.南京军区装备部军械装甲部，江苏 南京 210016；3.解放军63981测试计量队，湖北 武汉 430311）

0 引 言

落点偏差预测是弹道修正的关键技术之一，它是实施弹道修正的依据，预测算法的精度和实时性直接影响弹道修正的效果。本文对基于摄动理论的落点偏差预测算法进行了研究，对该落点偏差预测算法进行了误差分析并采取措施提高预测算法精度。

1 摄动落点偏差预测算法

根据摄动理论，实际弹道在基准弹道附近作小振幅“摆动”，因此可将射程、横偏函数在基准弹道上做泰勒展开，得纵向、横向预测落点偏差ΔL、ΔH，计算公式为[1-2]

x、y、z、νx、νy、νz——预测时刻弹丸实际位置、速率信息；

ΔL（R）、ΔH（R）——泰勒展开的高次项。

对于火箭弹这种弹道特性良好、实际飞行弹道偏离基准弹道较小的弹种，相比其他基于积分简化的弹道微分方程（4D弹道）的落点预测算法，它精度高、运算量小、实时性好。

2 摄动落点偏差预测算法误差分析

以某型火箭弹为例，通过蒙特卡罗打靶（1024条弹道）分析摄动落点偏差预测算法误差，仿真条件如下：

（1）射程：28.5km；

（2）火箭弹密集度指标：Ex/X=1/170，Ez/X=1/100；

（3）火箭炮射击准确度指标：0.3%X；

（4）落点偏差预测时刻：弹道时间60 s。

结果显示，预测算法纵向误差平均值-1.37176，标准差2.593 825；横向误差平均值-0.13381，标准差2.529 139。可以看出，算法精度很高，能够对落点偏差进行精确预测。

上述的落点偏差预测算法虽然精度较高，但这是在不计入弹道测量误差前提下得出的。而进行落点偏差预测离不开弹道测量，弹道测量误差对落点偏差预测算法的精度有直接影响，因而需要分析引入弹道测量误差后落点偏差预测算法的精度。

本文采用BD2卫星导航系统测量实际弹道数据，为此本节引入BD2测量误差。根据摄动落点偏差预测算法原理，算法误差主要与BD2的水平定位误差、定高误差、水平定速误差、垂直定速误差相关。

BD2测量误差设定为

（1）水平定位误差：8m（1σ）；

（2）定高误差：15m（1σ）；

（3）水平定速误差：0.3m/s（1σ）；

（4）垂直定速误差：0.4m/s（1σ）。

在预测落点时，加入BD2测量随机误差，即

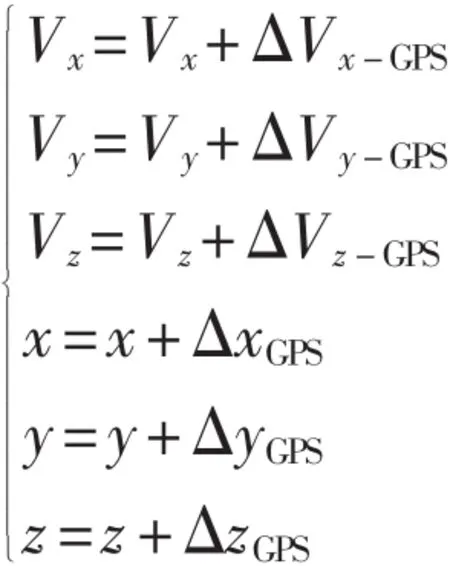
仿真条件与之前相同，对1024条弹道的统计结果如图1所示，引入BD2误差后，预测算法纵向误差平均值-0.16067，标准差13.95959；横向误差平均值-0.923 86，标准差10.826 1。可以看出，引入BD2误差后，落点偏差预测算法误差大幅增加。

3 卡尔曼滤波

从以上分析可知，BD2误差对摄动落点偏差预测算法误差有较大影响，因此需要采取措施消减BD2随机误差，以保障摄动落点偏差预测算法的精度。

综上所述，本文主要是在财务管理视角下进行高新企业税收筹划研究，旨在实现两者的共同发展，从财务管理角度出发，能保证企业税收筹划目标的合理制定，进而为企业战略目标的实现提供有效途径。要想做好财务管理视角下的税收筹划，本文提出灵活应用税法环境、高效处理会计工作等措施，可在这些措施有效实施下，实现高新企业税收筹划效果的提升，从而提高企业运营效益。

本文采用卡尔曼滤波解决上述问题[3]。考虑到摄动落点偏差预测算法以质点弹道数据（x、y、z、νx、νy、νz）预测落点偏差，因此本文采用质点弹道模型作为弹道滤波和外推弹道的状态方程。

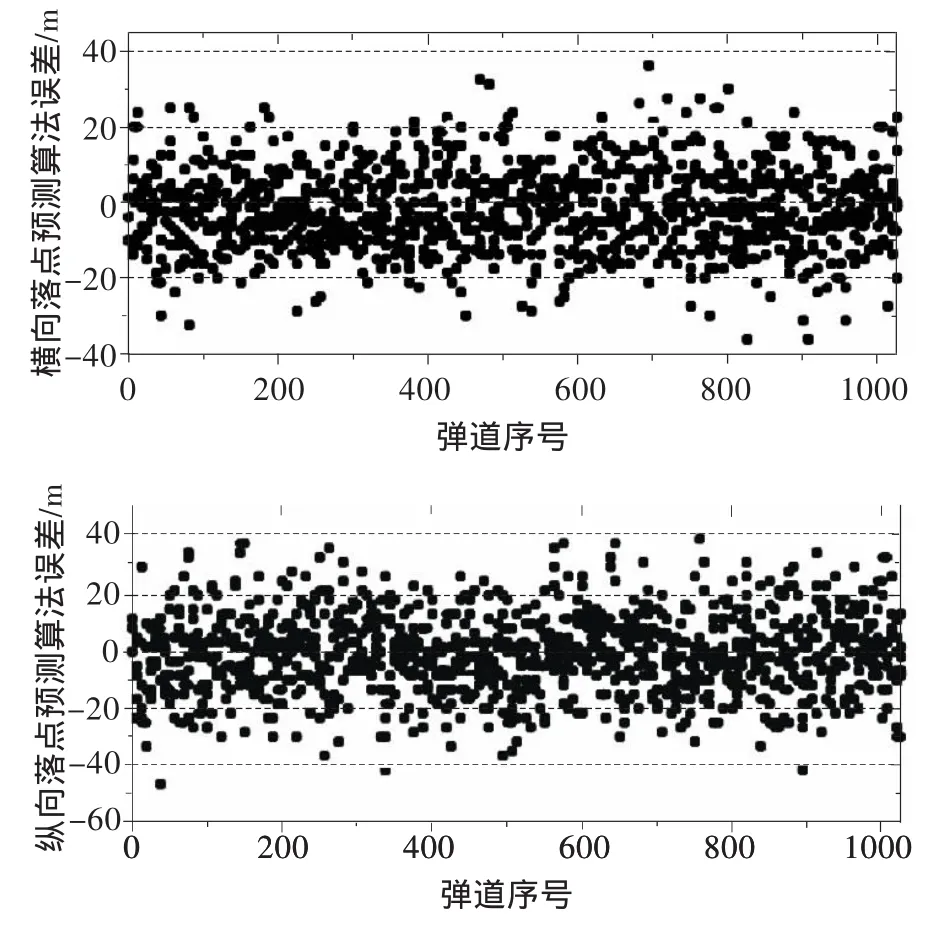
图1 摄动落点偏差预测算法误差

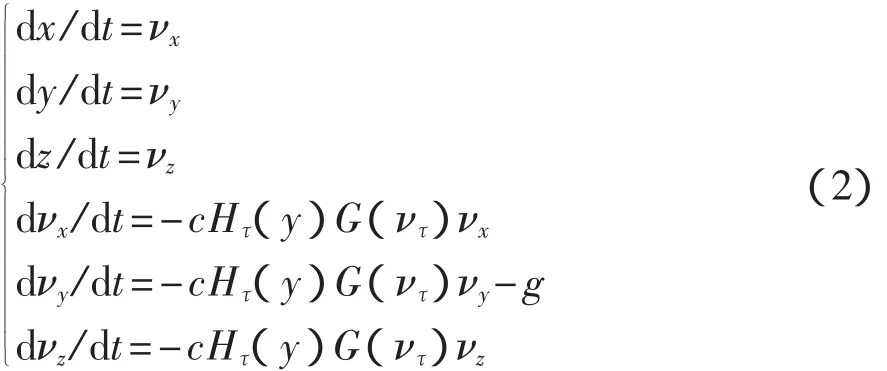
式中：x、y、z、νx、νy、νz——火箭弹在地面坐标系中的坐标分量和速度分量；

c——弹道系数；

G（ντ）——阻力函数；

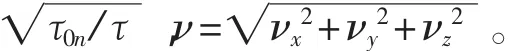
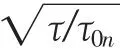
取 x、y、z、νx、νy、νz作为卡尔曼滤波的状态变量，即

式中：V（t）为高斯随机误差，6维列向量。

假设已对观测量实施从WGS-84坐标系到发射坐标系的转化，对于3-D弹道模型，观测量即为对状态量 x、y、z、νx、νy、νz的测量值，因此量测方程可写为

式中：Zk——k时刻的6维量测向量；

Hk——k时刻的量测矩阵；

Xk——k时刻的6维状态向量；

Vk——k时刻的6维量测噪声，其标准差等于GPS量测误差标准差。

状态一步预测方程为

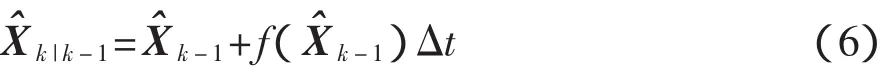
一步预测均方误差为

状态估值方程为

均方误差估值方程为

滤波增益方程为

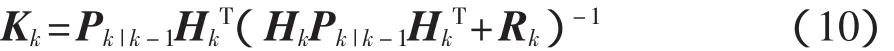
Pk|k-1——的均方误差阵；

Φk/k-1——k-1时刻到k时刻的一步转移矩阵；

Rk——k时刻测量误差协方差阵。

以某型火箭弹为例，引入BD2误差，采用BD2测量数据进行落点偏差预测，某弹道的落点偏差预测结果如图2所示。采用卡尔曼滤波后的BD2测量数据进行落点偏差预测，某弹道的落点偏差预测结果如图3所示。

从图2、图3可知，采用卡尔曼滤波后的弹道测量值进行落点预测，可使落点偏差预测算法误差大幅减小。对1024条弹道的统计结果显示，采用卡尔曼滤波后，横向落点偏差预测误差均值为-0.481 89，标准差为4.525 895，纵向落点偏差预测误差均值为-0.98424，标准差为5.467 926，预测精度较高，可为实施弹道修正提供准确依据。

图2 预测算法误差（滤波前）

图3 预测算法误差（滤波后）

4 结束语

本文研究了摄动落点偏差预测算法，并对预测算法进行了误差分析，针对引入弹道测量参数随机误差后预测算法误差较大的问题，建立了卡尔曼弹道滤波模型对弹道测量数据进行滤波处理，以消除弹道测量随机误差，提高摄动落点偏差预测算法的精度。仿真试验表明，采用卡尔曼滤波后，摄动落点偏差预测算法精度明显提高。

[1]雍恩米，唐国金.基于摄动制导的弹道导弹发射诸元的仿真算法[J].系统仿真学报，2005，17（5）：1048-1051.

[2]刘洁瑜.导弹惯性制导技术[M].西安：西北工业大学出版社，2010.

[3]刘建业.导航系统理论与应用[M].西安：西北工业大学出版社，2010.