层次信息可视化在区域规划中研究与应用

沈伟 李伟波

摘要：以区域发展规划可视化技术及软件为背景，结合了区域规划中信息表示的问题，分析了几种表示区域规划信息的层次信息可视化方法，提出了基于目录树和双曲树表示的层次信息结构，最后实现了层次信息可视化技术应用于区域规划，为区域规划的制定和实施提供了可视化导航。

关键词：区域规划；信息可视化；目录树；双曲树

中图分类号：TP311文献标识码：A文章编号：1009-3044(2012)20-4879-06

Research & Application of Hierarchical Information Visualization for Regional Planning

SHEN Wei, LI Wei-bo

(School of Computer Science & Technology,Wuhan Institute of Technology,Wuhan 430073, China)

Abstract: Based on visualization technologies and software of regional planning, the essay combines with regional planning issues of infor mation expression, analyses the several methods of hierarchical information visualization to express the information of regional planning, makes the hierarchical information software architecture based on directory tree and hyperbolic tree, finally realizes hierarchical information visualization technology used in the regional planning, provides visualized navigation for the draft and implementation of regional planning. Key words: regional planning; hierarchical information visualization; hyperbolic tree; directory tree; hyperbolic tree

目前，随着社会不断的快速发展，一些城市或区域面临着新的发展契机，因此如何重新来定位新的发展规划就显得越来越重要，但是传统的纸质版的区域规划方案已经不能适应新时代的要求，将计算机可视化技术应用于区域规划是解决问题的唯一方法。

区域发展规划内容的表述是一项大型而且复杂的工程，而且规划的内容也在不断的发生变化。因此，如何在这海量数据中获取有效信息成为信息可视化技术的研究热点之一。在信息结构中，树形结构是应用比较多的。但是，对于区域发展规划中这种大型的层次结构而言，采用树形结构不能将所表示内容整体呈现。针对上述的问题，该文以区域发展规划可视化技术及软件为背景，在分析研究层次信息可视化技术的基础上，提出了双曲树结构的可视化表示方法，并且着重研究了基于目录树和双曲树结构的区域规划层次信息可视化的实现方法。

1信息可视化的分析

可视化技术是指运用图像处理技术和数据库技术，将数据转换成图形或图像在计算机屏幕上显示出来，并进行交互的技术。信息可视化技术就是利用计算机对抽象数据的可视表示，用来加强人们对这些抽象数据的直观认识[1]。

抽象信息之间的关系最普遍的一种就是层次关系。层次关系无处不在，如磁盘目录结构，文档管理，图书分类等。传统的描述层次信息的方法就是将其组织成一个类似于树的节点连线图，这也是层次信息可视化结构最直观的方式。但是这种树型结构对于大型的层次结构而言，树型结构的层次就会交织在一起，不利于展示层次信息，特别是用计算机表示树型结构时，由于计算机屏幕所提供的可视化空间有限，大型的树型层次结构，只能通过滚动浏览的方式把整个层次结构显示出来，这对于展示某个树型结构的整个层次结构信息或某个节点的信息就可能不是很方便[3]。

随着人们对层次信息可视化技术的深入研究，也推出了一系列的可视化技术方法。其中，由Xerox Palo Alto研究中心用界面的John Lamping等人提出了一种基于双曲几何的可视化和操纵的大型层次结构的Focus+Context，即称为双曲树，在表示大型的层次结构中，应用最多。双曲树结构是将层次关系显示在一个双曲平面上，然后将双曲平面映射到显示的区域中。双曲树结构的出现很好地解决了怎样在用户屏幕上显示庞大的层次信息结构的问题。

2区域规划的层次信息可视化结构的设计

2.1信息可视化的表示模型

该文提出来的可视化表示方法是将区域规划中的这一领域层次信息结构，抽象成目录树结构和双曲树结构，然后将目录树结构映射层目录树视图或双曲树视图来表示区域规划这一领域层次信息，最后通过用户与目录树或双曲树视图进行交互获取领域信息的过程。如图1，图2所示。

2.2目录树模型设计模型

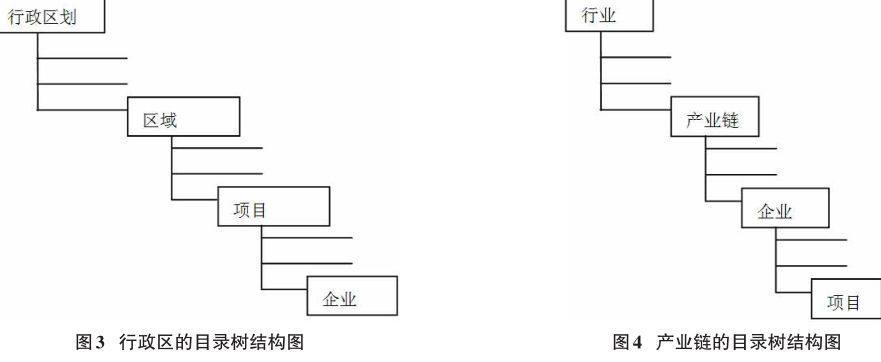
在区域规划中，其领域层次中以行政园区和产业链划分。树形结构按预设的行政区块（行政区、区域、项目、企业）或产业链（行业、产业链、企业、项目）逐级表示行政园区层次信息，如图3，图4所示[5]。

目录树结构显示区域规划中领域信息的层次化列表。目录树层次结构的顶端是根，层次结构的根的下一层是子项，子项下面是其子项，构成四层父子关系。子项以缩进方式显示在父项的下面，项目之间用线段连接起来。

目录树的数据结构如图5所示。

图5目录树的数据结构

创建目录树结构的关键代码如下：

void CPrjBrowseView2::CreatTree()

{ m_ctrlTree.DeleteAllItems();

m_TreeBootImage.DeleteImageList();

CPrjBrowseApp * pApp = (CPrjBrowseApp *)AfxGetApp();

CPrjBrowseDoc* pDoc = (CPrjBrowseDoc*)GetDocument();

//Tree控件变量

HTREEITEM hParent;

TVINSERTSTRUCT tvInsert;

tvInsert.hParent = NULL;

tvInsert.hInsertAfter = NULL;

tvInsert.item.mask = TVIF_TEXT;

//创建图象标签

m_TreeBootImage.Create(16,16,ILC_COLORDDB | ILC_MASK,4,0);

if(m_tabData.GetCurSel() == 0)

{

m_nImgCardClose = m_TreeBootImage.Add(pApp→LoadIcon(IDI_CARDCLOSE));

m_nImgCardOpen = m_TreeBootImage.Add(pApp→LoadIcon(IDI_CARDOPEN));

}

else if(m_tabData.GetCurSel() == 1)

{

m_nImgCardClose = m_TreeBootImage.Add(pApp→LoadIcon(IDI_CARDCLOSE1));

m_nImgCardOpen = m_TreeBootImage.Add(pApp→LoadIcon(IDI_CARDOPEN1));

}……

//添加子目录

int nTab = m_tabData.GetCurSel();

if(m_tabData.GetCurSel() == 0)

AddSubTree("DH_00_00_00_00","1","行政单位",hParent); //添加子目录

else if(m_tabData.GetCurSel() == 1)//sw05.03

AddSubTree("CL_00_00_00_00","1","行政单位",hParent); //添加子目录

m_ctrlTree.Expand(hParent,TVE_EXPAND); //展开Tree目录

SetTimer(2,100,NULL);

SetTreeNode();

}

2.3双曲树模型设计

双曲树模式的设计原理是：双曲空间焦点的周围的区域在圆面上大面积显示，远离焦点的区域以远景图的形式慢慢消失在圆面的边缘上。在圆面上，随着半径的增加，节点对象尺寸就变得越来越小，而圆面边缘对应双曲空间上有无限的空间，可以存放大量节点对象。在双曲空间中，通过布局为每个节点分配了相同大小的显示区域，因此当任何一个节点被置为视图焦点的时候，此节点都会在圆面中有较大的显示区域，而远离新焦点的区域会消失在圆面的边缘上[2]。

双曲空间只是一个抽象的空间,人们直观上很难理解，在双曲空间中完成布局后，就必须用一种方法将双曲空间里的结构映射到欧氏空间的二维平面，双曲空间是一个无限空间，计算机显示屏是一个有限空间（欧几里德空间）。双曲空间转换欧几里德空间是通过庞莱卡投影来实现。

一般把通过庞莱卡投影得到的圆面称为庞莱卡圆盘(Poincare Disk)模型，具有以下属性:

①模型区域S={(x,y)|x2+y2<1}，即圆盘是欧几里得空间中半径为1的圆；

②双曲几何角度和欧几里得几何角度一样，故庞莱卡投影又称等角投影；

③双曲空间的直线对应欧几里得空间垂直S的弧线，或者过S中心的直线。两个没有交点的弧线对应于双曲平面中的两条平行线。

映射算法把双曲空间某节点映射到扇形区域(r, d)的中心，所谓的扇形区域中心即图6中的C点。设半径为1,(r, d)扇形区域两个端点的坐标为(cosr, sinr)和(cos(r + d), sin(r + d))，那么中心点的坐标是:

Cx = (1/cos(d/2)-tan(d/2)) * cos(d + d/ 2)

Cy = (1/cos(d/2)-tan(d/2)) * sin(d + d/ 2)

然后运用递归算法将所有节点、结构按照以上的映射方式从双曲空间映射到欧几里德空间里[4]。

图6庞莱卡圆盘映射

双曲树的数据结构如图7所示。

图7双曲树的数据结构

布局双曲树结构的关键代码如下：

void CPrjBrowseDoc::layoutHyperbolicTree()

{if(m_pTreeNode != NULL)

{m_pTreeNode→m_nSelState = 1;

double dfOff = 0.02;

m_pTreeNode→m_dfCX = dfOff;

m_pTreeNode→m_dfCY = dfOff;

m_pTreeNode→m_dfLX = dfOff;

m_pTreeNode→m_dfLY = dfOff;

double dfAngle0 = m_pTreeNode→m_dfAngle + PIE / 6;//PIE - 0.5;//m_pTreeNode→m_dfAngle * 2.0;//1.5;

double dfStart0 = m_pTreeNode→m_dfStart - PIE / 12.0;//+ m_pTreeNode→m_dfAngle / 2 - (PIE- 0.5) / 2.0;// * 0.5 / 2; if(dfAngle0 < 0)

dfAngle0 += 2 * PIE;

if(dfStart0 < 0)

dfStart0 += 2 * PIE;

if(m_pTreeNode == &m_TreeNode)

{ dfAngle0 = 2 * PIE;

dfStart0 = 0.0;

m_pTreeNode→SetPoincareOrgPos(0,dfStart0,dfAngle0);

}

else

{double dfOff = 0.20;

m_pTreeNode→m_nLayerPos = fabs(dfOff);

double R0 = m_pTreeNode→GetR2(m_pTreeNode→m_nLayerPos); double R1 = R0 - 1.0 / 10.0;

m_pTreeNode→m_dfCX = R0 * cos(dfStart0 + dfAngle0 / 2);

m_pTreeNode→m_dfCY = R0 * sin(dfStart0 + dfAngle0 / 2);

m_pTreeNode→m_dfLX = R1 * cos(dfStart0 + dfAngle0 / 2);

m_pTreeNode→m_dfLY = R1 * sin(dfStart0 + dfAngle0 / 2);

m_pTreeNode→SetPoincareOrgPos(m_pTreeNode→m_nLayerPos,dfStart0,dfAngle0);

CTreeNode * pTreeNode = m_pTreeNode→m_pParent;

if(pTreeNode != NULL)

{double dfStart = dfStart0 + dfAngle0 + dfAngle0 / 4;

double dfAngle = 2 * PIE - dfAngle0 - dfAngle0 / 2;

pTreeNode→m_nLayerPos = __min(0.20,fabs(pTreeNode→m_nLayerPos - dfOff));

double R0 = pTreeNode→GetR2(pTreeNode→m_nLayerPos);

double R1 = R0 - 1.0 / 10.0;

pTreeNode→m_nLayerPos = 1;

pTreeNode→m_dfCX = R0 * cos(dfStart + dfAngle / 2); pTreeNode→m_dfCY = R0 * sin(dfStart + dfAngle / 2); pTreeNode→m_dfLX = R1 * cos(dfStart + dfAngle / 2); pTreeNode→m_dfLY = R1 * sin(dfStart + dfAngle / 2);

pTreeNode→SetPoincareOrgPos2(pTreeNode→m_nLayerPos,dfStart,dfAngle,m_pTreeNode);

}}}}

2.4目录树与双曲树相互转换

目录树结构和双曲树结构，是一个层次信息两种表示方法。这两种方法各有所长各有所短。目录树结构在表示层次信息时，是按照人们通常习思维方式表示信息的，具有比较直观的特点。双曲树结构表示层次信息是当层次结构非常大时,在有限的屏幕上很难全面地显示整个信息，采用焦点十上下文(Focus+Context)的视图变换方法，可以在显示一个小的焦点区域详细信息的同时，保持整个内容的整体视图，使用户很容易访问上下文信息并能定位到自己所需要的信息。这两种方法在获取焦点信息时，显示的内容是统一的，即时在一方展示某一方面的信息，在另一方同样展示该信息。

3层次信息可视化技术在区域规划中应用

目前，层次信息可视化技术应用于区域规划中，以潜江城市转型发展规划为例，如图8所示，图中展示了以行政区划分的目录树结构和双曲树结构图。在目录树中，鼠标左键点击“周矶高新产业园”，就展开了其子项下的五个项目名称，在其双曲树图中，“周矶高新产业园”也随着放大，展开了其子项。同理，在双曲树中鼠标左键点击“周矶高新产业园”，原理一样[5]。

再如图9所示，图中展示了以产业链划分的目录树结构和双曲树结构图。在目录树中，鼠标左键点击“支柱产业”，就展开了其子项下的4个产业链目录，在其双曲树图中，“支柱产业”也随着放大，展开了其子项。同理，在双曲树中鼠标左键点击“支柱产业”，原理一样。

图9产业链的目录树和双曲树的可视化转换

从上面两个图中，可以直观的观察出双曲树结构表示的大量的层次信息时，有巨大的优势。双曲树结构中，将选中的层次信息放大显示出来。既可以从整体控制整个信息结构，又可以局部放大所需的层次信息。

4结束语

随着信息可视化技术的不断成熟和发展，可视化技术已经成为了近年来研究的热点问题之一。该文以区域发展规划可视化技术及软件研究为前提，分析了层次信息可视化技术，具体设计和实现了目录树结构和双曲树结构的可视化表示方法，最后通过将层次信息可视化技术应用于区域规划中，最终为区域规划的制定和实施提供了可视化导航。

参考文献：

[1]邓满英.信息可视化探讨[J].软件导刊.2008,7(9):99-100.

[2]窦长威.层次信息可视化技术一种实现方法[J].工程地理计算机应用.2007(46):11-15.

[3]崔军,贾宗维,王建伟,于慧娟.一种新的层次信息可视化模型[J].山西农业大学学报:自然科学版,2009,29(2):186-189.

[4]何杨,李伟波,胡维平.层次信息可视化集成技术的应用[J].武汉工程大学学报,2011,33(10):90-94.

[5]沈伟.基于知识工程的区域规划DSS关键技术研究[D].武汉:武汉工程大学,2011:42-44,57-64.