两种参数转换模型在福州1∶500测图项目中的应用及分析
2012-04-29宋珂
该文以福州1:500测图工程为例,对WGS84坐标系统的大地坐标转换到福州城市坐标系统中的平面直角坐标,采用同一软件分别求取七参数和四参数进行精度分析,由此得到小范围内使用四参数和高程拟合优于七参数的精度。
椭球转换;七参数;四参数;精度
【作者简介】宋珂(1982—),男,河南商丘人,航测外业项目经理,现任西安煤航信息产业有限公司测绘工程院助理工程师。
1.坐标系的分类
空间大地坐标系。以参考椭球面为基准面的大地坐标。大地经度是通过某点大地子午面和起始大地子午面间的夹角,大地纬度是通过某点的法线与赤道面间的夹角,大地高是某点沿法线方向到参考椭球面的距离。
空间直角坐标系。空间直角坐标系的坐标原点在参考椭球的中心,Z轴指向参考椭球的北极,X轴指向起始子午面和赤道的交点,Y轴位于赤道面上且按右手系与X轴成90度夹角。某点在空间中的坐标可用在此坐标系的各个坐标轴上的投影来表示。
平面直角坐标系。平面直角坐标系是利用投影变换将空间坐标通过某种数学变换眏射到平面上,投影变换的方法有多种,对于大比例尺地形图来说通常用的是高斯-克吕格投影。高斯投影是一种横、椭圆柱面、等角投影,椭圆柱面与参考椭球在轴子午线上相切,就是平面直角坐标系的X轴,地球的赤道在椭圆柱上的投影即为Y轴,将椭圆柱面展开就得出高斯投影平面直角坐标系。为减少投影变形,高斯投影分为3按海縺按及任意分带。
地心坐标系。地心坐标系的坐标原点是地球质心,表示某点位置的纬度是该点位到参考椭球中心和赤道面的夹角,经度、高度的表示和空间大地坐标系相同。
2.坐标系统及转换模式
A.常用坐标系
我们常用的GPS接收机接收的星历参数是基于WGS84坐标系统下。目前测量成果普遍使用的是1954年北京坐标系统、1980西安坐标系统、地方(任意)独立坐标系统,这几种坐标系之间不但坐标原点不一致,而且各坐标轴之间互不平行,还存在的尺度比例不统一,作业时通常采用参数互转。
B.转换基本模式
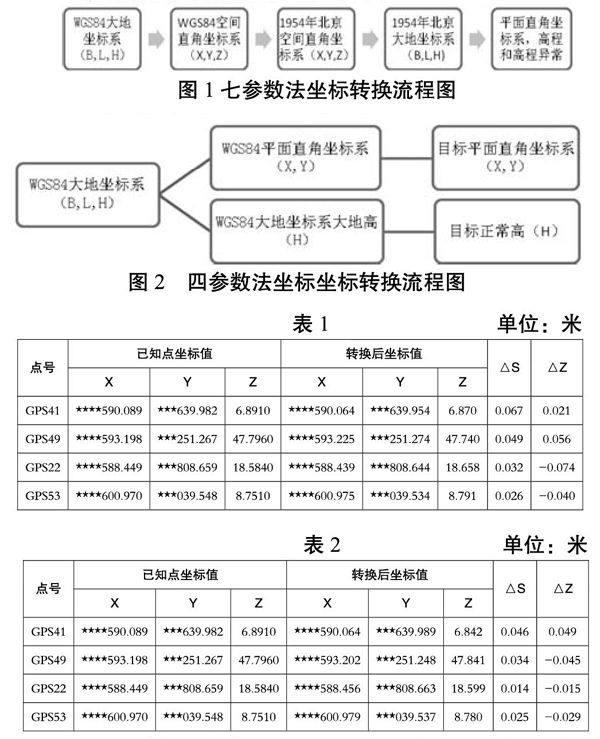
七参数转换。其流程图如图1所示。
两个不同大地坐标系转换通常采用布尔莎公式转换,以空间直角坐标系作为衔接。求取参数同名点最少为3个,转换数学模型不再赘述,按最小二剩法原理求解七个转换参数。
四参数转换。其流程图如图2所示。
基本原理是通过投影后经过旋转、尺度、平移和常用的高程拟合取得目标平面坐标和高程,转换数学模型不再赘述,按最小二剩法进行求解。
高程拟合根据范围和点数选择合适的方式,使用3个已知高程点进行计算时,高程拟合易采用加权平均的方法;使用4到6个已知高程点时,高程拟合易采用平面高程拟合的方法;使用7个以上已知高程点时,高程拟合易采用曲面拟合的方法。
3.利用七参数模型和四参数模型求解数据实例分析
项目介绍。本项目测图比例尺1∶500,面积约5平方公里,成图平面坐标系统是福州城市地方平面直角坐标系,高程系是罗零高程系。需求由WGS84系统到福州城市独立坐标系统下的一套参数。有9个已知点分别有两套系统下的成果,分布情况良好。
七参数模型转换及精度比较。由5个起算点GPS38、GPS39、GPS44、GPS46、GPS50、按最小二剩原理求取七参数,然后采用参数转换GPS41、GPS49、GPS22、GPS53做精度检查,比较结果见表1。
数模型转换及精度比较。用同样5个起算点GPS38、GPS39、GPS44、GPS46、GPS50、按最小二剩原理求取四参数,高程求取采用高程平面拟合法。然后采用参数转换GPS41、GPS49、GPS22、GPS53做精度检查,比较结果见表2。
两模型比较结果论述。在小范围内从七参数模型和四参数模型求的数据精度看出,四参数模型求得结果优于七参数模型求得结果,由此用实例证明小范围用四参数比较合适。从椭球定位的特性和经验得出在小于30公里范围内时易采用四参数模型,在大于30公里范围时易采用七参数模型。
4.结束语
在航测成图和城市建设及工程测量中坐标系统有着广泛的应用,根据测量范围的大小、控制点的分布情况选择合适的转换方式对成果精度的提高非常重要,本文从实例中证实了在小范围测量时用四参数模型的优越性。
二维转换模型中由于椭球参数不一致会引起不同坐标轴方向的尺度比不一致,以及控制网的坐标误差在不同的坐标轴方向有差异,如果在模型中采用两个尺度因子求算出四参数则精度会更高。
[1]祥元,郭际明,刘宗泉.大地测量学基础.武汉:武汉大学出版社,2006
[2]王解先,王军,陆彩萍.WGS-84与北京54坐标的转换问题.大地测量与地球动力学,Vol.23,No.3,2003.08
[3]刘亚平,郑若奇,曹立强.GPS定位中两种七参数坐标转换方法的误差分析
