List流上的log熵函数

马冰清,潘全香

（1.河南师范大学 数学与信息科学学院,河南 新乡 453007；2.河南科技学院,河南 新乡 453003）

List流上的log熵函数

马冰清1,潘全香2

（1.河南师范大学 数学与信息科学学院,河南 新乡 453007；2.河南科技学院,河南 新乡 453003）

Ricci流的Perelman泛函的log熵函数与黎曼流形上的log Sobolev不等式密切相关.List流是比Ricci流更加广泛的一种几何流,由于它与广义相对论之间关系密切而成为了研究热点.主要定义了对应于List流的一种新的log熵函数,并计算了其关于时间t的第一变分公式,对其单调性也进行了讨论.

List流；熵函数；单调性

2006年,著名数学家Perelman以Ricci流为工具证明了著名的Poincare猜想,这使得Ricci流成为一个非常热的研究方向.为了研究Ricci流的奇性,很多时候需要引入一些熵函数,并利用熵函数的单调性等性质研究Ricci流的奇性问题.借助于log熵函数与Perelman泛函之间的关系,Ye在[1]中定义了log熵函数并研究了其单调性及在流形上的log Sobolev不等式.另外,log熵函数与log Sobolev不等式的梯度形式也密切相关.Wu在[2]中对log熵函数在热方程上也进行了研究,并研究了其单调性.

为了建立与广义相对论之间的联系,List引入了List流,它是一种比Ricci流更加广泛的几何流[3]. List流也具有类似的Perelman泛函.本文给出了List流上的log熵函数的定义,及其具有类似Perelman泛函的单调性公式.

1 log熵函数的第一变分公式

设(M,g(t))是n维紧致的黎曼流形,g(t)是下面的List流的一个解

其中α＞0是常数,φ=φ(t)是Mn上的光滑函数,△是对应于g(t)的Laplacian算子.明显的,如果φ是常数,则List流方程（1）变为了Ricci流方程

因此,List流是Ricci流的一个自然推广.令Sij=Rij-αφiφj是一个对称的2阶张量,则式（1）可以写为

设S=gijSij=R-α|∇φ|2是2阶张量Sij的迹,则有

定义1定义下面的log熵函数

更加一般的,可以定义下面的带有参数a的log熵函数

定义2定义下面更加广泛的log熵函数

明显的,Ya(g,u)=Ya(g,u ,0).

接下来,研究对应List流的log熵函数式（3）的第一变分公式,并讨论它的单调性.定义u=e-f,则对于List流的微分系统

式（4）中第三个方程保证了

利用式（2）得到

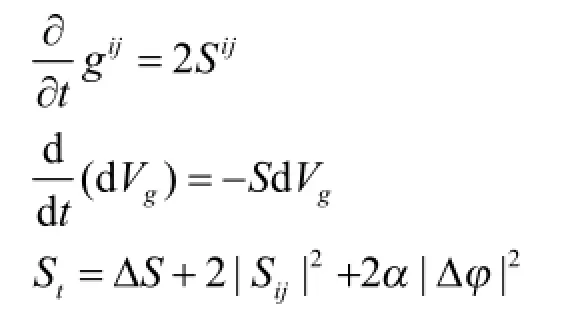
其中（gij）是（gij）的逆矩阵,Sij=gikgjlSkl.令

注意到

则有

利用Sij的定义以及第二Bianchi恒等式,得到

因此

把Bochner公式

和式（6）代入式（5）,得到了

注意到u=e-f,那么ft=-Δf+|∇f|2-S 等价于

并且式（3）变成了

直接计算可得

则有

因此,得到了下面的结果：

定理1假定E+4a＞0,则在系统（4）下,以下结论成立

如果φ是常数,则从定理1得到了对应于Ricci流的log熵函数的单调性公式,见文献[4].关于对应于List流的梯度Shrinking Soliton的定义,见文献[5].

2 小结

本文定义了对应于List流的一种新的log熵函数,并计算了其关于时间t的第一变分公式.由于熵函数与log Sobolev不等式联系密切,因此所得到的结果必将对List流上log Sobolev不等式的研究提供有力的理论基础.另外,所研究的log熵函数与List流上的Perelman泛函有很多相似之处,因此结果也会促进对Perelman泛函的几何研究.

[1] Ye R G.The Log entropy functional along the Ricci flow[J/OL].arXiv：0708.2008.[2012-10-18].http://arxiv.org/abs/0708.2008.

[2] Wu J Y.The logarithmic entropy formula for the linear heat equation on Riemannian manifolds[J].Nonlinear Anal,2012,75（13）：4862-4872.

[3] List B.Evolution of an extended Ricci flowsystem[J].Comm.Anal.Geom,2008,16（5）：1007-1048.

[4] Li J F.First variation of the Log entropy functional along the Ricci flow[J/OL].arXiv：0712.0832.[2012-10-18].http://arxiv.org/abs/0712.0832.

[5] Yang F,Shen J F.Volume growth for gradient shrinking solitons of Ricci-harmonic flow[J].Science China Mathematics,2012,55（6）：1221-1228.

（责任编辑：卢奇）

The log entropy functional along the List's flow

Ma Bingqing1,Pan Quanxiang2
（1.College of Mathematics and Information Science,Henan Normal University,Xinxiang 453007,China；2.Henan Institute of Science and Technology,Xinxiang 453003,China）

The relationship between the log entropy functional corresponding with the List's flowand the log Sobolev inequality on Riemannian manifolds is close.List's flowhas been a hot which is a natural generalization of the Ricci flowbecause of its closely connection to general relativity.In this paper,a newlog entropy functional has been defined,and then we compute its first variation.On the other hand,we study its monotonicity.

List's flow；entropy functional；monotonicity formula

O186.12

A

1008-7516（2012）06-0044-04

10.3969/j.issn.1008-7516.2012.06.010

2012-11-5

国家自然科学基金（11171368）；河南省自然科学基金（092300410143）

马冰清（1978-）,女,河南商丘人,硕士,讲师.主要从事微分几何、概率论等方面的研究.